边坡动力响应规律探讨

赵体，陈运飞，田维

（1.北京市公联公路联络线有限责任公司，北京 100161；2.北京市路政局道路建设工程项目管理中心，北京 100031；3.国核电力规划设计研究院，北京 100095）

岩土工程

边坡动力响应规律探讨

赵体1，陈运飞2，田维3

（1.北京市公联公路联络线有限责任公司，北京 100161；2.北京市路政局道路建设工程项目管理中心，北京 100031；3.国核电力规划设计研究院，北京 100095）

振型代表了边坡岩土体在某一频率地震荷载作用下质点振动强弱的空间分布，是弹性波在边坡岩土体内传播规律的一种映像。通过模拟场地地脉动信息，研究边坡在微振作用下的振动特征，了解边坡自振规律，依据边坡地震动力稳定性分析系统的基本模块探讨边坡微振型分布和边坡破坏规律的内在联系，推断边坡在遭遇未来强震作用时可能发生破坏的部位及边坡体可能出现的破坏方式。

边坡；振型；动力响应；破坏规律

1 研究概况

岩土边坡动力特性研究是岩土工程和地震工程研究的重要课题之一［1-5］。徐光兴等［6-7］开展了1∶10比例尺的边坡大型振动台模型试验研究，通过调整地震动输入参数，研究了边坡模型在地震荷载作用下的动力特性与动力响应规律；刘汉龙等［8］考虑在地震过程中边坡安全系数曲线的波动变化过程，建议采用最大振幅的0.65倍作为平均振幅来表征边坡的安全系数；陈玲玲等［9］建立了评价岩质陡高边坡地震稳定性计算公式，结合工程实例，计算了潜在滑裂面的抗剪断强度储备比值；吴兆营等［10］提出一种适合于岩体边坡安全系数非线性分析方法，建立了加权平均安全系数的概念；郑颖人等［5］、谭儒蛟等［11］、毕忠伟等［12］结合有限差分的方法对边坡的动力问题也做了大量研究。目前研究大多集中在边坡在地震荷载作用下的受迫振动特性和地震动力破坏特性研究，对岩土体边坡的自振特性研究较少，全面考虑边坡在地震荷载作用下的状态变化及破坏规律，应该深入了解岩土边坡的自振特性与边坡在未来强震作用下的受迫振动特性及地震破坏方式之间的联系。因此研究边坡在微振作用下的振型分布，通过对边坡场地地脉动信息的数值模拟，揭示边坡自振特性。根据振动理论，当地震动的频率与岩土边坡的固有频率接近时，边坡岩土体振动强度最强，即产生共振现象，这是造成边坡地震破坏的一个重要因素。因此，对岩土边坡的自振特性展开研究，是深入认识边坡动力特性（包括共振特性）的基础环节；其二是探讨边坡微振型分布与边坡破坏规律的联系，根据振型所揭示的边坡岩土体振动强度分布规律，推断边坡在遭遇未来强震作用时，可能发生破坏的部位及可能出现的破坏方式，研究开展对边坡地震稳定性分析具有重要的理论和实践意义。

本文选取陕西宝鸡地区某黄土边坡进行了探讨。

2 边坡动力响应数值分析

2.1 数值模型建立

边坡位于宝鸡市金台区渭河北岸四级阶地，阶地内堆积物为二元结构，物质均匀单一，性质稳定，边坡为正东方向倾斜的单面缓坡，坡面走向近南北，现场地脉动测试结果显示，边坡的卓越频率为2.5Hz，根据边坡勘察资料，将岩土介质概化为3层（如图1），力学参数如表1。边坡数值分析采用有限差分软件进行［13］，本构模型采用Mohr-Coulomb弹塑性本构关系，不考虑水的影响。

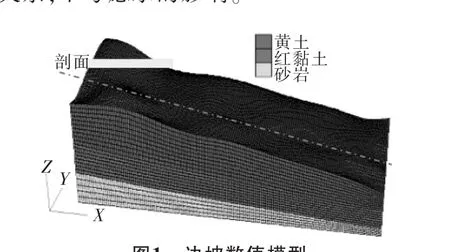
图1 边坡数值模型

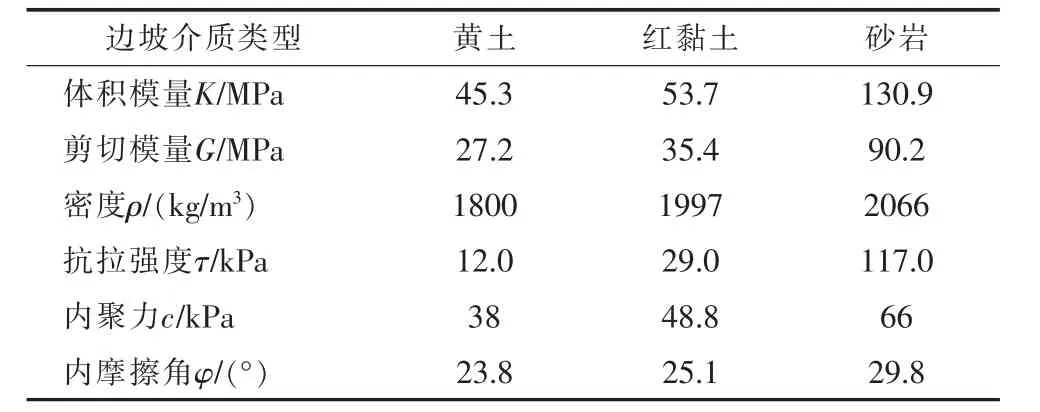
表1 边坡数值计算物理力学参数

模型以地理坐标（107°06′16″E，34°24′49″N）为坐标原点，X轴指正东方向（EW向），Y轴指正北方向（NS向），Z轴垂直向上（UD向）。

模型以X轴方向取1052m，Y轴向取413m，底部边界取至588m高程。

2.2 边坡微振特性分析

为揭示边坡的自振特性，对岩土体边坡模型底部施加三向（EW、NS、UD）地震荷载，微振频率选取边坡卓越频率2.5Hz，简谐振动峰值加速度为1.0×10-5g，模拟场地地脉动的“白噪音”特性，进而揭示边坡的自振特性。

根据祁生文［14］、徐光兴等［7］研究结论，当边坡体内波场稳定时，简谐波持时对边坡动力响应影响不大，本文激振时间取T=16s，使边坡产生受迫振动，模型底部采用静态边界，四周采用自由场边界，待波场稳定后，加速度（绝对值）最大值展布状态如图2。

图2 最大值（三分量）分布云图

由图2数值看出，当边坡底部受到2.5Hz简谐波激振时，各质点在3个方向上均出现了明显的振动强度分区，加速度最值呈条带状分布，随着边坡高程的升高，呈现出节律性变化规律，在坡顶的陡倾部位出现了最值，反映了凸出地形对荷载的放大作用；这实质上反映了波场在岩土体内传播相干叠加的规律，是边坡地层条件、波动传播方式等因素综合作用的结果。

2.2.1 卓越振型

在边坡进行微振动激励的过程中，激振频率选取边坡的卓越频率2.5Hz，如果称振动响应最强烈的边坡振型为卓越振型，则该边坡的卓越振型为2.5Hz振型，在此振动频率下，边坡的振动强度最强，较好地揭示了边坡的自振强度分区特性。

2.2.2 波场

边坡在某一频率“白噪音”振动激振下，表现出特定的振型，这实质上是边坡岩土体中波场的一种映像。这一结果主要受到边坡形态、尺度、地震动输入方式及波动频率（波长）等因素的制约。因此，不同的波场分布可能会对应不同的工况组合形式。深入了解波场的分布规律，需要深入认识波动在边坡体内的传播规律，这是边坡动力响应分析研究中值得关注的领域。

2.2.3 振动强度

根据微振分析的结果可以看出，边坡岩土体波动强度出现频繁的空间交替变化现象，这一现象与边坡岩土体内的波动相干叠加有关。即使在微弱的振动条件下，坡体后缘及地形高度变化较大的陡倾面附近始终是振动强度最剧烈的部位，反映了振动能量的累积，这种分布规律与边坡破坏失稳方式密切相关。随着振动强度的进一步增强，这些部位必然成为坡体滑动的启动部位。

2.3 边坡破坏方式分析

考虑地震波垂直入射到边坡模型底部，模型质点在水平面内（沿X轴）振动，保持微振阶段的介质参数及边界条件不变，通过由弱到强的逐步提高地震动激振强度的方法，搜索边坡破坏失稳的临界地震峰值加强度及破坏失稳状态［4］，对边坡的自振特性和边坡在未来潜在地震作用下的破坏方式展开比对。

当输入地震动峰值加速度ap增加到280cm/s2时，坡体后缘及地形高度变化较大的陡倾面附近出现大面积塑性区，并逐渐连片贯通，出现了贯通的塑性带，根据边坡失稳塑性区贯通的判别原则，可以推断边坡已经开始失稳，边坡失稳时塑性区分布状态如图3。

图3 边坡塑性区分布图

2.4微振振型展布与破坏方式相关性分析

对比边坡在微震作用下的加速度最大值（三分量）分布云图与边坡破坏时的塑性区分布状态可知，坡体凸出的陡倾面附近始终是边坡振动强度最大部位，当地震荷载增加到一定程度时，这些部位率先产生破坏失稳迹象，成为坡体滑动的启动部位，为了更加清晰地揭示边坡自振强度分布与塑性区分布位置关系，选取典型截面加速度最大值（如图4）与塑性区分布（图5）展开比对，截面位置如图1。

图4 2.5Hz激振作用时典型截面上加速度最大值（三分量）分布云图

图5 典型截面上塑性区分布

由图4可知，地震动波射线垂直射入边坡体内，当遇到地质界面时，会产生连续的反射与叠加现象，波动强度在局部区域会产生增强与减弱，根据数值分析的结果可以看出，弧形界面底部一定深度内（约25m）3个方向均出现了加速度最大值，振动强度较四周明显剧烈，从能量传播角度来讲，即形成了能量汇聚区，此时，坡顶陡倾部位弧形界面表现为明显的“凹面镜”效应，而坡面凹地形底部加速度最值相对较小，表现为“凸面镜”效应。因此可以推断，当边坡遭遇地震动作用时，坡顶凸起的陡倾部位必然是边坡发生破坏失稳的启动部位，而坡面凹地形则相对安全。这种推断也得了图5的验证，其自振强度强弱状态和塑性区分布状态取得了较好的对应关系。

这种现象可以从介质中弹性波的传播理论得到解释，如图6，当一行垂直入射的地震波射线遭遇边坡自由表面时，根据snell定律，会在地质界面处产生反射和透射现象［15］，由于边坡上部自由表面地形的起伏变化，反射的波射线会产生汇集和发散现象，具体表现为在凸起地形下部形成能量汇聚区（Collect-ing area），凹地形下部形成能量发散区（Divergence area），据此可以推断，当边坡遭遇地震动时，由于凸起部位底部能量的集聚，将率先遭到破坏，凹地形则相对安全。

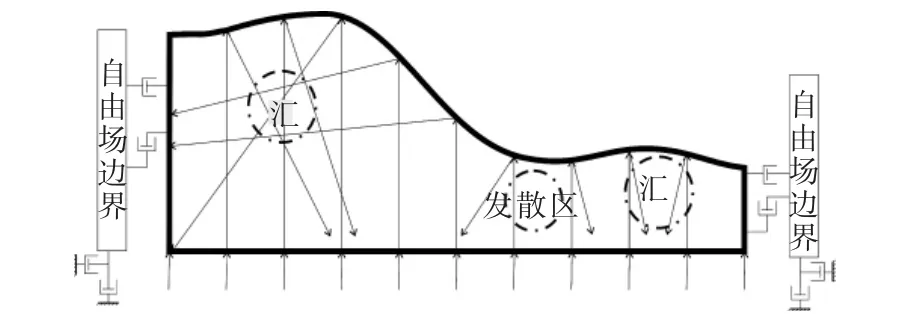
图6 单层介质弧面模型射线路径示意图

3 结语

（1）边坡的自振特性研究是边坡动力特性研究的一个重要方面。边坡自振特性与边坡形态、体量大小、岩土性质、地质结构等自身性状条件密切相关，边坡在微振作用下表现出明显的振动强度分区，呈现出明显的节律性变化规律，这是波场在边坡岩土体中的一种映像；研究岩土边坡的自振特性对深入认识边坡的受迫振动特性及地震破坏方式具有重要的理论指导意义。

（2）振型代表了边坡岩土体在某一频率地震荷载作用下质点振动强弱的空间分布，是波动在岩土体内传播过程中相干叠加的结果，即使边坡在微弱振动作用下，凸起部位始终是振动强度最大的部位，呈现出明显的“凹面镜”效应，在凸起部位底部一定深度范围内形成能量汇聚区，当能量累积到一定强度时，将有可能率先发生滑动，而凹地形下部形成能量发散区，则相对安全，这对于边坡地震稳定评价及工程抗震设防具有重要的理论和实践意义。

（3）边坡自振特性与边坡破坏规律的联系，是工程边坡地震动力稳定性分析系统的基本模块之一。随着研究的深入，针对同一边坡，还应考虑地震作用方式变化对应的边坡地震破坏方式多样性的研究。

［1］孙进忠，陈祥，王余庆.岩土边坡地震崩滑的三级评判预测［J］.地震研究，2004（3）:256-264.

［2］王欢，车爱兰，葛修润，等.岩质高边坡动力稳定性评价方法与应用［J］.上海交通大学学报，2011（5）:706-710，715.

［3］蒋金泉，张培鹏，聂礼生，等.高位硬厚岩层破断规律及其动力响应分析［J］.岩石力学与工程学报，2014（7）:1366-1374.

［4］赵体.岩土边坡地震稳定性临界加速度分析方法研究［D］.北京：中国地质大学，2012.

［5］郑颖人，叶海林，黄润秋，等.边坡地震稳定性分析探讨［J］.地震工程与工程振动，2010（2）:173-180.

［6］徐光兴，姚令侃，高召宁，等.边坡动力特性与动力响应的大型振动台模型试验研究［J］.岩石力学与工程学报，2008，27（3）:624-632.

［7］徐光兴，姚令侃，李朝红，等.边坡地震动力响应规律及地震动参数影响研究［J］.岩土工程学报，2008，30（6）:918-924.

［8］刘汉龙，费康，高玉峰.边坡地震稳定性时程分析方法［J］.岩土力学，2003，24（4）:553-557.

［9］陈玲玲，陈敏中，钱胜国.岩质陡高边坡地震动力稳定分析［J］.长江科学院院报，2004，21（1）:33-35.

［10］吴兆营，薄景山，刘红帅，等.岩体边坡地震稳定性动安全系数分析方法［J］.防灾减灾工程学报，2004，24（3）:237-241.

［11］谭儒蛟，李明生，徐鹏逍，等.地震作用下边坡岩体动力稳定性数值模拟［J］.岩石力学与工程学报，2009，28:3986-3993.

［12］毕忠伟，张明，金峰，等.地震作用下边坡的动态响应规律研究［J］.岩土力学，2009，30（S1）:180-184.

［13］陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例［M］.北京:中国水利水电出版社，2009.

［14］祁生文.边坡动力响应分析及应用研究［D］.北京:中国科学院地质与地球物理研究所，2002.

［15］胡聿贤.地震安全性评价技术教程［M］.北京:地震出版社，1999.

The discussion of slope dynam ic response

ZHAO Ti1，CHEN Yun-fei2，TIANWei3
（1.Beijing Gonglian Road Tie-line Co.，LTD.1，Beijing 100161，China；2.Roadway Construction ProjectManagement Center of Beijing Municipal Roadway Administration Bureau，Beijing 100031，China；3.State Nuclear Electric Power Planning Design&Research Institute，Beijing 100095，China）

Vibration type represents the distribution of vibration intensity for a slope under a certain frequency seismic load，which is a result of the coherent superposition for elastic waves in a slope.Two questions are disscussed in this paper，one is the vibration characteristics of the slope under the action ofmicro vibration，which is a foundation to study dynamic characteristics for slopes and a basic module for slope stability owing to earthquake actions.The second one is to discuss the link between vibration types and the rules of slope failure，in order to imagine the site of damage and failure mode for a rock and soil slope under the action of strong earthquakes thatmay occur in the future，which is significant for the dynamic stability analysis of slopes.

slope；vibration type；dynamic response；failure rule

U416.14

A

1672-9900（2015）01-0072-04

2014-12-01

赵体（1983-），男（汉族），河南南阳人，工程师，主要从事岩土动力工程学研究，（Tel）13581617714。