铜//水纳米流体导热系数分子动力学研究

邱腾蛟 王浩昌

（华北水利水电大学，河南 郑州 45500004455）

纳米流体的这一概念由美国Argonne国家实验室的Choi［1］等人在1995年首次提出，即以一定的方式和比例将纳米尺度的金属或金属氧化物粒子悬浮于液体基液中，形成的一类新型的传热冷却工质［2］。近些年来，纳米流体成为了国内外的研究热点。国内外许多学者的实验研究结果表明，纳米流体的导热性能相对于其基液会有一定程度上的改善，具有广阔的应用前景。分子动力学模拟作为研究纳米流体的重要方法，被越来越多地应用于纳米流体强化传热机理的研究［3］。

目前许多学者从实验和宏观方面对纳米流体强化传热进行研究，包括不同纳米颗粒、不同体积分数等因素对传热的影响［4］，但从微观角度研究纳米颗粒对基液导热性能影响的文献还相对较少。本文以铜/水纳米流体为对象，利用平衡分子动力学（EMD）方法模拟纳米颗粒与基液的相互作用，探究纳米流体强化传热的机理，并且通过改变体系的温度观察其对导热系数的影响。

1 模拟方法

所谓分子动力学（Molecular Dynamics）模拟，是指对于原子核和电子所构成的多体系统，用计算机模拟原子核的运动过程，从而计算系统的结构和性质，其中每一原子核被视为在全部其他原子核和电子所提供的经验势场作用下按牛顿定律运动［5］。在模拟过程中，通过求解每个分子在其他所有分子作用下的牛顿运动方程，得出每个分子的位置和速度，从而得出系统内分子随时间的运动过程，最后通过统计学的方法得出宏观参数。由于MD方法从最基本的物理定律出发，只要模拟系统中粒子的初始坐标和速度确定，以后每一时刻所有粒子的位置和速度便已确定，所以MD模拟方法是一种确定性模拟方法［6］。

本文使用MS和LAMMPS两种软件结合起来进行分子动力学模拟，首先利用MS软件建立Cu纳米颗粒与基液H2O的纳米流体模型，其中H2O采用SPC模型，分子间作用势采用Lennard-Jones（L-J）势能函数，图1给出了L-J势能函数曲线图。

L-J势能函数形式如下：

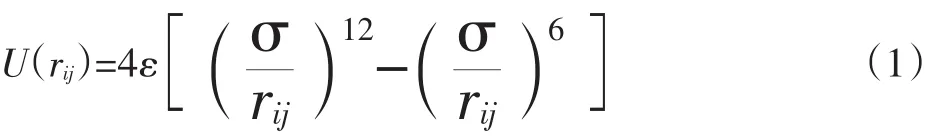
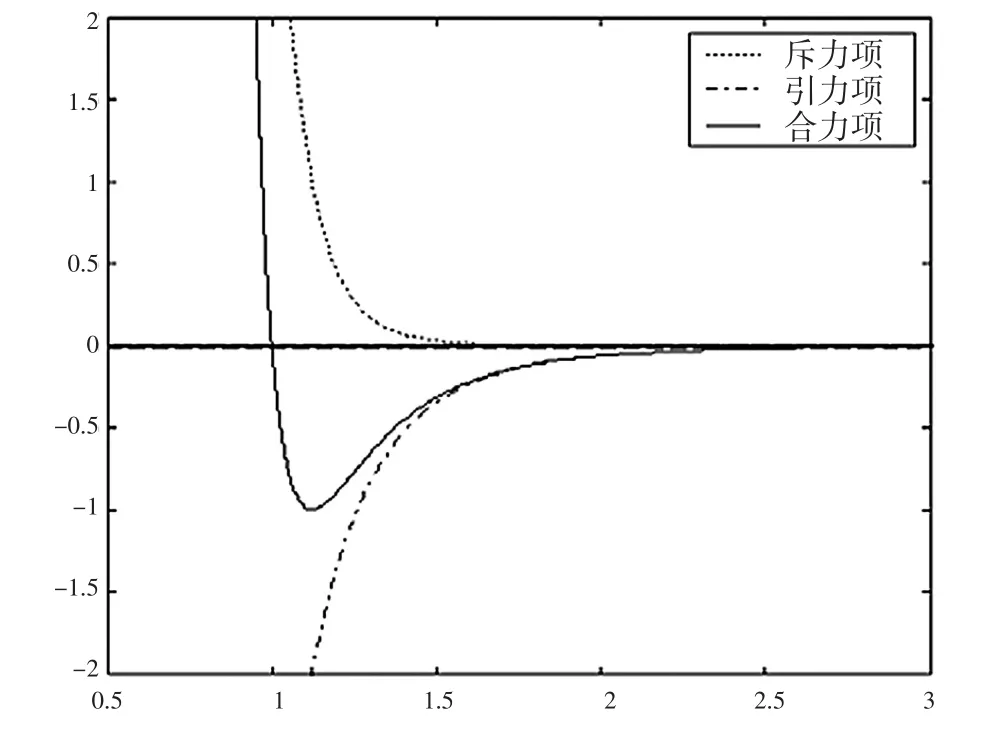
图1 L-J势能函数曲线图

式中，Yij为粒子i与粒子j之间的距离，ε和σ分别为L-J势能函数的能量参数和长度参数。式中第一项表示分子间的短程排斥力，第二项表示分子间的远程吸引力（如范德瓦耳斯力等）。

由于不同的粒子含有不同的能量参数和长度参数，而本文所涉及的纳米流体为两项混合，因此要选取合理的混合法则。目前在分子动力学模拟中普遍采用的混合法则为Berthlot混合法则［7］，其形式如下：

式中，l代表流体相，s代表固体相。本文中用到的数据见表1。

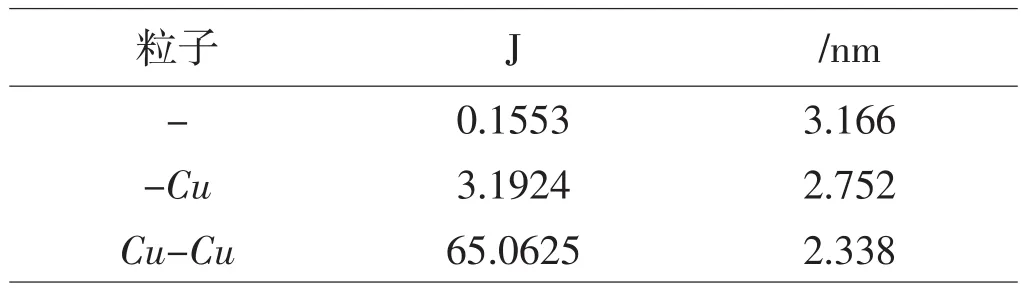
表1 Cu/H2O相互作用L-J势能参数

其次，根据MD模拟基本理论［8］，导热系数可通过积分微观热流量的自相关函数得到，其Green-Kubo公式为：

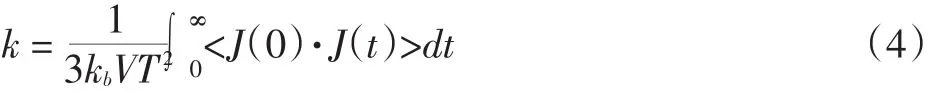
式中：V为体积，T为温度，为波耳兹曼常数，为相对于某个0时刻的t时刻的流体的热流密度；式中用尖括号表示系综平均，即取模拟计算总时间的平均值，为热流自相关函数。

利用所选参数通过LAMMPS进行分子动力学模拟，模拟过程中所有参数均进行无因次化处理，模拟过程采用周期性边界条件，使得模拟盒子内粒子始终保持不变，截断半径选取为3.5。在系综选取中采用NVT正则系综，即在模拟过程中体系的粒子数、体积和温度保持不变，通过虚拟热浴使得体系维持于特定温度的平衡状态。对于运动方程的求解，则采用目前应用比较广泛的Velocity-Verlet算法。

2 模型的建立及结果

2.1 Cu/H2O纳米流体模型的建立

此纳米流体以水作为基液，首先需建立起水分子的模型，运用MS提供的工具，绘制出水分子的结构，调整元素及氢氧键键角得到水分子结构如图2所示（其中中间原子代表氧原子，两侧原子代表氢原子）。

图2 水分子模型

其次，从MS的模型库中导入铜晶体模型，如图3所示。然后以此为基础，选择球形体系建立起直径为1.5nm的球形纳米颗粒，如下图4所示。

图3 铜晶体模型

图4 铜纳米颗粒模型

最后，利用水分子模型、铜纳米颗粒模型以及MS软件中的AC模块，建立包含1 375个水分子的Cu/H2O纳米流体模型，边界条件选为周期性边界条件，颗粒的体积分数为3%。模型如图5所示。

图5 Cu/H2O纳米流体模型

2.2 模拟过程及结果

根据上述建立的纳米流体模型，采用开源的MD模拟程序LAMMPS进行模拟计算。首先为了验证分子动力学方法计算导热系数的可靠性，采用纯水建立模型进行分子动力学模拟，得到纯水在温度为298K时的导热系数为0.586 2，与实验值的相对误差为3.45%，因此验证了模拟计算具有可靠的精度。其次，对体积分数为3%的铜/水纳米流体进行分子动力学模拟计算，计算导热系数的输入文件须进行单独编写，设定初始条件，对整个体系进行模拟计算并得到输出结果。在分子动力学模拟计算中，模拟体系的系统选为正则系统（NVT），模拟温度为290～340K，模型中所有粒子初始时按照面心立方结构（FCC）排布，初始速度根据Maxwell-Boltzmann分布随机取样，初始速度方向为随机取向，边界条件采用周期边界条件，每次模拟过程采用800 000时间步长，其中前600 000个时间步长为系统弛豫过程，使系统达到稳定，后200 000步用于统计导热系数及相关量，每一个时间步长取为0.001ps。

如图6给出了体积百分比为3%铜/水纳米流体导热系数增加比随温度变化关系。从图中可以看出，纳米流体的添加使得流体的导热系数得到明显的提高，并且在相同的体积百分比下，随着温度升高纳米流体的导热系数增加比例呈现增大趋势。

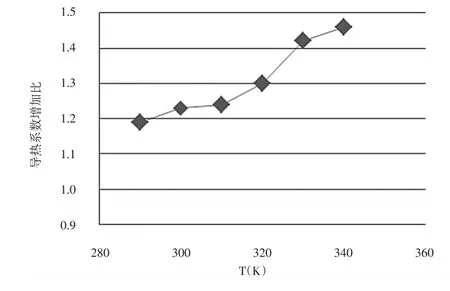
图6 导热系数随温度的变化

3 纳米流体强化传热机理的分子动力学模拟分析

径向分布函数（RDF，RadialDistribution Function）是指任一给定原子在距离为r处的平均数密度与在同样的总密度情况下的理想气体中某原子在距离为r处的密度之比，其定义式为：

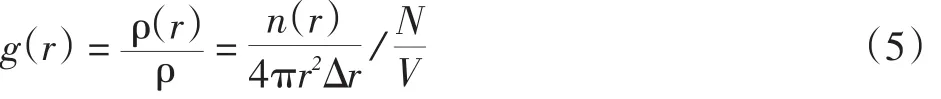
式中：n（r）为距离为r到之间的粒子数。

径向分布函数是表征流体和非晶态固体微观结构特征的一个特征物理量，对于本文所涉及的Cu/H2O纳米流体的固液两相，可以有效地判别固体纳米颗粒对于基液的作用。图7给出了体积分数为3%的含球形铜纳米颗粒的水基纳米流体在300K时的径向分布函数，从图中可以看出，添加了球形铜纳米颗粒后，纳米流体的微观结构发生了明显的改变：径向分布函数在0.97nm处和1.49nm处出现了两个明显的峰值，并且最后逐渐震荡收敛于1，表现出了纳米流体“短程有序，长程无序”的典型特征，同时也揭示了纳米颗粒表面存在着吸附层，并且包含有两层，两层吸附层大小约为0.36nm和0.25nm。

图7 Cu/H2O纳米流体径向分布函数

纳米颗粒表面吸附层是影响纳米流体强化传热的重要因素。一般情况下，固体的导热系数比液体的导热系数高得多，这主要因为固体内部的分子排列比液体内部分子排布更加规则；而纳米颗粒的添加使得纳米颗粒与基液分子之间发生作用，使得纳米流体的微观结构发生变化，从而产生了两层纳米颗粒表面吸附层，使得在纳米颗粒表面的基液分子排布得更加规则均匀，形成了类似于晶体的结构。一方面，由于吸附层的排列更加地均匀，因此吸附层应该具有比基液更高的导热系数（介于纳米颗粒与基液之间），当热量在基液与纳米颗粒之间传递时，纳米颗粒表面吸附层就相当于一层具有低界面热阻的表面，有利于热量扩散作用的进行；另一方面，在纳米颗粒表面形成的排布更加规则、类似固体的吸附层，这就相当于变相增加了纳米颗粒的径粒，使得纳米颗粒的有效径粒增大，从而变相增加了纳米颗粒的体积分数，最终导致了纳米流体导热系数的增加。

4 结语

本文使用分子动力学的方法，以Cu/H2O纳米流体为研究对象，详细介绍了Cu/H2O纳米流体的建模过程，并对体积分数为3%的Cu/H2O纳米流体的导热系数以及纳米颗粒与水基液的相互作用进行了研究分析，得到了以下结论：

①Cu纳米颗粒的添加使得纳米流体的导热系数得到了明显的提高，并随着纳米流体体系温度的升高，纳米流体的导热性能也得到增强。

②通过分子动力学模拟的方法，对Cu/H2O纳米流体的径向分布函数进行分析，发现了纳米流体微观结构的变化，证明了纳米颗粒表面吸附层的存在。

③本文从纳米颗粒表面吸附层的角度分析了纳米流体强化传热的机理，为进一步研究和分析纳米流体的导热系数，提供了一种方向和基础。

［1］US Choi.Enhancing Thermal Conductivity of Fluids with Nanoparticles ［C］//Developments and Applications of Non-Newtonian Flows.ASME，NY，1995：99-105.

［2］王楠，陈俊，安青，等.纳米流体分散稳定性的分子动力学研究初探［J］.工程热物理学报，2011，32（7）：1107-1110.

［3］宣益民，李强.纳米流体能量传递理论与应用［M］.北京:科学出版社，2010.

［4］LI X F，ZHU D S，WANG X J.Evaluation on Dispersion Behavior of the Aqueous Copper Nano-Suspensions［J］.Journal of Colloid and Interface Science，2007，310（2）:456-463.

［5］文玉华，朱如曾，周富信，等.分子动力学模拟的主要技术［J］.力学进展，2003，33（1）：65-73.

［6］崔文政，白敏丽，吕继组，等.纳米流体应用于内燃机冷却水腔强化传热的导热机理分析［J］.内燃机学报，2013，31（6）：557-563.

［7］M P Allen，D J Tildesley.Computer Simulation of Liquids［M］.Oxford：Clarendon Press，1987.

［8］陈俊.纳米流体输运性质作用机理的分子动力学模拟研究［D］.北京：清华大学，2011.