人工鱼群算法在水土流失监测中的应用

于　苗，谢　翔（山东绿景水土保持工程设计咨询有限公司，山东 济南 250101）

人工鱼群算法在水土流失监测中的应用

于苗，谢翔
（山东绿景水土保持工程设计咨询有限公司，山东 济南 250101）

【摘要】本文将时间序列分形维计算方法引入到青岛胶南国电电力子罗风电场土壤流失监测序列复杂性诊断中，并结合人工鱼群算法对数据幂律关系进行智能高效的拟合，确定了监测序列土壤流失复杂性指标——分维值的大小，结果表明：青岛胶南国电电力子罗风电场土壤流失监测序列复杂性具有风机站区及施工道路区最高、升压站区最低、集电线路区居中的分区特征，且子罗风电场实际生态环境在很大程度上影响土壤流失监测序列复杂性分布。

【关键词】人工鱼群算法；水土流失；分维值；水土监测

近年来，随着《水土保持法》的不断深入贯彻，区域水土流失的预测分析逐步成为水土保持学研究的热点。在自然变化及人类活动的干扰下，水土资源要素越来越明显地表现出其自身的随机性、混沌性等复杂性特征。水土流失过程是一个随时间变化的、连续的过程，其大尺度内的复杂性变化可以通过分形理论的标度不变性反映和体现小尺度的特征。因此，用分维值定量表述其过程线的复杂程度及流失量多少的变化过程，探究影响水土流失复杂性的多种复杂性驱动因子。

分维值的计算方法主要有Hausdorff维数法、盒子维数法、重标度极差分析法、标尺法、半方差法、PSD法以及根据测度关系、相关函数、分布函数等求分维的方法。对于给定的时间序列模型，识别其分形维数特征问题已经被不同领域的许多学者所提出并解决。到目前为止，基于曲线长度的时间序列分形维数法在水土流失过程的复杂性测度中应用还很少，本文应用该方法对度量风电场工程中水土流失的复杂性，以揭示水土流失地域地形差异的复杂性。

1　研究区概况与资料来源

1.1研究区概况

国电电力胶南子罗风电场位于青岛胶南市理务关镇吉利河水库沿岸子罗村附近，南北长约3.8m，东西最长约4.5m，面积约16.36m2。地理坐标为：东经119°35'20"~119°38'55"，北纬35° 45'49"~39°47'32"。项目建设风力发电机组33台，需改建道路12.1km，新修道路16.5km，架设集电线路22.5km。项目总占地面积33.26hm2，其中永久占地面积2.90hm2，临时占地面积30.36hm2。项目区内总挖方49.37万m3，总填方46.04万m3，弃方3.33万m3（其中表土剥离量3.18万m3）。整个项目自然恢复期内水土流失防治分区分为风机站区、110kV升压站区、场内施工道路区、集电线路区。

1.2资料来源

本文选择国电电力胶南子罗风电场水土保持各防治分区作为研究对象。根据建设类项目自然恢复期一般为2年的规律，从山东省水文局搜集该风电场各水土流失防治分区 2011-05~ 2013-05（每月2次）土壤流失监测结果。对于搜集资料中个别防治分区缺失的水土流失监测资料数据，采用对称延拓法进行插值完善。绘制土壤流失监测序列变化曲线（2011—2013年），见图1。由图1可以看出，风电场各防治分区土壤流失监测序列随时间的推移，扰动侵蚀量呈现逐渐衰弱趋势，但雨季流失量普遍偏高。

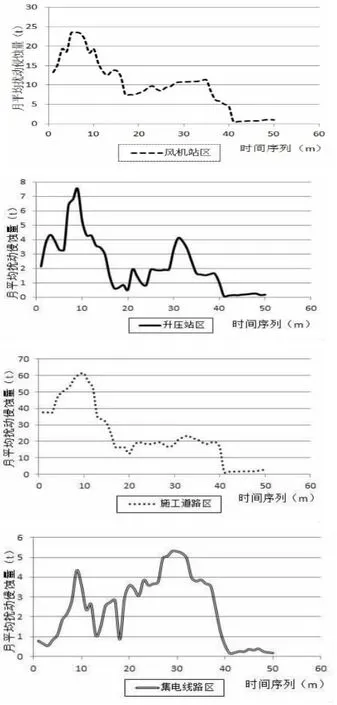
图1子罗风电场各水土流失防治分区土壤流失监测序列曲线2011-05～2013-05（每月2次）

2　测度方法

2.1基于曲线长度的时间序列分形维数法

分形理论被提出以来，在自然科学很多领域都取得了广泛的应用。然而对分形理论的研究，除了将其应用于拓扑对象中，时间序列也遵循分形几何特征规律——标度不变性。

一个时间序列分形维数D计算方法的可靠性与测量尺度的有限性密切相关。进行长序列研究必须要有大量的测量数据，并且在度量过程中进行动态趋势转变。因此，算法的迅速收敛成为有限次度量的时间序列分形维数计算的研究重点。

在时间尺度T下，n元动态过程yi，时间步长为Δt，将所测量数据按下列规则进行筛选、组合：

第一轮选择为所有测量的时间序列数据y1，y2，y3，…，yn-1，yn。第二轮选择数据时间间隔为2Δt，即：y1，y3，y5，…，yn-2，yn。若取L为所筛选相邻数据之间的k个距离之和，则有：

1）当时间间隔为Δt时，时间序列曲线长度L 为|y1-y2|+|y2-y3|+…+|yn-1-yn|；

2）当时间间隔为2Δt时，时间序列曲线长度L为|y1-y3|+|y3-y5|+…+|yn-2-yn|。

依此类推，时间序列曲线的长度依赖于测量的时间尺度Δtm=k*Δt，L~Δtm1-D，由于Δtm时间段与被分割的时间长度成反比，因此上述幂律关系可表达成L~k1-D，其中：k=（n-1）/m（m为分成的段数，n-1为总的时间序列长度）。根据上述幂律分布，绘制log（L）~log（k）图，利用最小二乘法求出斜率，进而可以得到分形维数D。

由于具有分形特征的事物服从幂律分布，即N（r）=Cr±D。因而在求解分形维数的过程中，往往通过最小二乘法拟合log（r）~log（N（r））曲线，求出斜率，进而得到分形维数。分形特点无标度区间的尺度范围通常很难确定，而最小二乘法是对所有观察的点对进行拟合，拟合结果往往会因标度区间以外无效点的引入而影响计算结果的准确率。本文采用施秋红等提出的简化的人工鱼群拟合方法对分形维数进行进一步求解。

2.2人工鱼群拟合优化算法

人工鱼群算(ArtificialFishSwarmAlgorithm，AFSA)是由李晓磊等在2002年提出的，通过模拟实际鱼群的运动、聚集等行为构造人工鱼，通过觅食、聚群及追尾行为改变自身的位置，一段时间的移动后各人工鱼在各极值处聚集，通过局部寻优找到全局最优值。这种优化技术，在解决优化命题的过程中引入了基于行为的人工智能思想，并通过动物自制体模式加以实现。

在实际的运算过程中，王联国等对人工鱼群算法模型中的视野Visual和步长Step按（1）式进行动态调整：

式中：Visual初值取xmax/4（xmax为最大搜索范围 ）；Step为visual/8，visualmin=0.001，stepmin= 0.0002；t为当前迭代次数；Tmax为最大迭代次数。

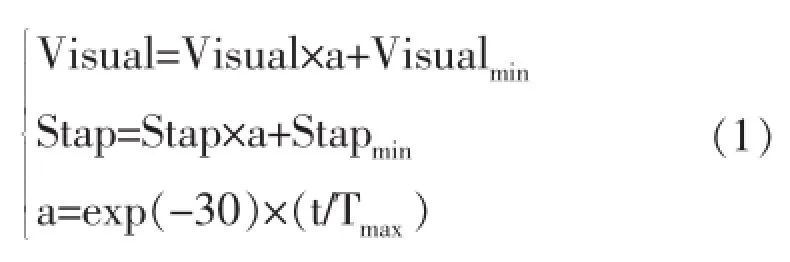
上述调整能够很好地平衡算法的全局或局部搜索能力，加快收敛速度，提高算法精度。在觅食行为中，人工鱼直接移动到视野内的较优位置，以加快搜索速度；在聚群行为中，用整个鱼群的中心位置代替邻域的中心位置；在追尾行为中，用群体最优位置代替邻域极值位置，不必再计算当前鱼与邻域所有人工鱼之间距离、邻域极值和邻域最优人工鱼与邻域内所有人工鱼之间距离，缩短了运行时间。

3　计算结果及分析

3.1子罗风电场土壤流失量分维值计算

根据现有子罗风电场各水土流失防治分区2011-05~2013-05（每月2次）土壤流失监测结果（长度n=50），采用前述时间序列分形维数计算方法对各水土流失防治分区土壤流失量进行分维值计算，同时采用上述人工鱼群拟合方法拟合L~AkD-1幂律关系，如表1所示。

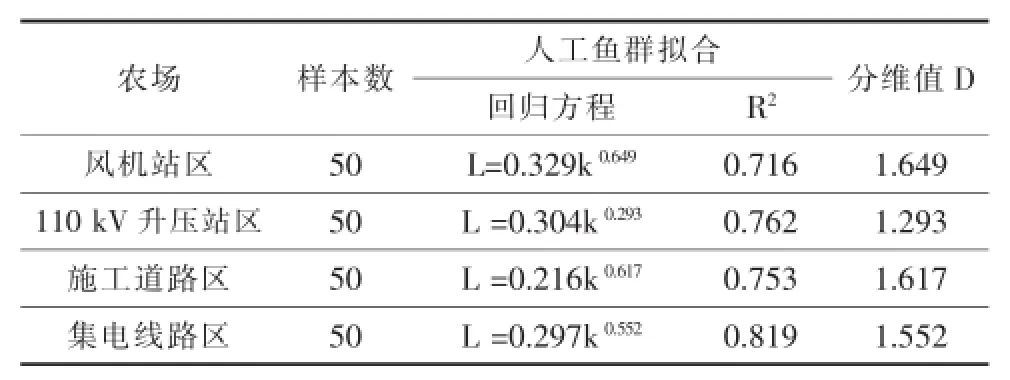
表1子罗风电场各水土流失防治分区土壤流失量复杂度分维计算结果及回归方程

从表1中可以看出，人工鱼群拟合效果明显，利用人工鱼群拟合得到的回归方程中各分区差异度系数A均低于0.4，其中施工道路区和集电线路区的差异度系数均低于0.3，说明拟合曲线与实际曲线差异度较小，拟合效果良好；另外，人工鱼群方法拟合各回归曲线的复相关系数平方（R2）值均达到0.7以上，回归方程相关性显著，从而保证了复杂性分析结果的准确性。分维值是分形理论的核心，也是度量系统复杂性的重要指标，分维值越大，系统越复杂，分维值越小，系统越简单。从表1中计算结果可知子罗风电场各水土流失防治分区土壤流失量复杂性综合排序为：风机站区>施工道路区>110kV升压站区>集电线路区。

3.2分维值空间分布结果特征分析

由表1可知，风机站区土壤流失量监测序列复杂性分维值等级最高，其次是施工道路区，说明这些区域影响土壤流失量变化的因子较多，复杂性相对较强；110kV升压站区和集电线路区复杂性分维值等级较低，说明这些区域的土壤流失影响因子较少，相关的降水复杂性相对较弱。

事实上，影响土壤流失的因素很多，除了季风、降雨等因素外，还有地形、森林覆盖面、下垫面人类活动及各种因素的综合作用。本文研究区域国电电力胶南子罗风电场位于青岛胶南市南部，风机站区位于风电场范围内山脊位置，海拔较高；110kV升压站区位于风电场山脚平原区，场内施工道路及集电线路连接于各风机安装平台之间。其中山丘、山脊位置土层覆盖较薄，不利于植被生长，加上局部地势高差较大，导致降雨对风机站区土壤冲刷严重，水土流失复杂性较高。相比之下，升压站区地势平坦，扰动土地面积较小，且植被覆盖率较高，不易造成土壤流失，因此，其土壤流失复杂性分维值较低。综合各因素的影响，可以看出子罗风电场周边生态环境在很大程度上影响了土壤流失量复杂性分布结果。

4　结语

本文将时间序列分形维计算方法引入到青岛胶南国电电力子罗风电场土壤流失监测序列复杂性诊断中，并结合人工鱼群算法对数据幂律关系进行智能高效的拟合，确定了监测序列土壤流失复杂性指标——分维值的大小，结果表明：青岛胶南国电电力子罗风电场土壤流失监测序列复杂性具有风机站区及施工道路区最高、升压站区最低、集电线路区居中的分区特征。通过进一步分析各分区地理构造，综合各种因素的共同影响，可以看出子罗风电场实际生态环境在很大程度上影响土壤流失监测序列复杂性分布结果。但由于该风电场土壤流失监测资料长度不足，复杂性测度结果的稳定性会受到一定影响，其他因素影响仍需进一步探究。

（责任编辑张玉燕）

【中图分类号】S157

【文献标识码】B

【文章编号】1009-6159（2015）-05-0064-03

作者简介：于苗（1987—），女，助理工程师