Representations of the Drazin inverse involving idem potents in a ring

（Department of Mathematics，Southeast University，Nanjing 211189，China）

Representations of the Drazin inverse involving idem potents in a ring

Zhu Huihui Chen Jianlong

（Department of Mathematics，Southeast University，Nanjing 211189，China）

An element a of a ring R is called Drazin invertible if there exists b∈R such that ab＝ba，bab＝b，and a－a2b is nilpotent．The element b above is unique if it exists and is denoted as aD．The equivalent conditionsof the Drazin inverse involving idempotents in R are established．As applications，some formulae for the Drazin inverse of the difference and the product of idempotents in a ring are given．Hence，a number of results of bounded linear operators in Banach spaces are extended to the ring case．

idempotent；Drazin inverse；spectral idempotent

L et R be an associative ring w ith unity 1．The symbols R－1，RDand Rnildenote the sets of invertible，Drazin invertible and nilpotent elements of R，respectively．The commutant of an element a∈R is defined as comm（a）＝｛x∈R：xa＝ax｝．Recall that an element a∈R is said to have a Drazin inverse［1］if there is b∈R such that b∈comm（a），bab＝b，a－a2b∈Rnil．The element b∈R above is unique if it exists and is denoted by aD．In this case，we call aπ＝1－aaDthe spectral idempotent of a．The nilpotency index of a－a2b is called the Drazin index of a，denoted by ind（a）．By RDwemean the setof all Drazin invertible elements in R．It is well known that a∈RDimplies that a2∈RDand（a2）D＝（aD）2．

Groβand Trenkler［2］considered the invertibility of pq for general matrix projectors p，q．Koliha and Rakocevic［3］studied the invertibility of the sum p＋q and described the relationship between the invertibility of p－q and p＋q for idempotents p and q in a ring．Later，Koliha and Rakocevic［4］obtained the equivalent conditions for the invertibility of p－q in a ring．

Many authors considered Drazin invertibility in different sets．For example，Deng［5］considered the Drazin inverse of the difference and the product of projections in Hilbert spaces．Deng and Wei［6］presented the formulae for the Drazin inverse involving idempotent bounded linear operators in Banach spaces．More results on the Drazin inverse of the difference and the product of idempotents can be found in Refs．［7- 9］．

In this paper，we present the formulae for the Drazin inverse of the difference and the product of idempotents in a ring．Moreover，the equivalent relationships of Drazin inverse involving idempotents are established．Hence，the results in Refs．［5- 6］are extended to a general ring case．Note that dimensional analysis and spectral decompositions cannot be used in a ring case．The results in this paper are proved by a purely algebraic method．

1 Some Lemmas

In what follows，p，q always mean any two idempotents in a ring R．We first state several known results in the form of lemmas．

Lemm a 1［10］Let S＝｛p－q，1－pq，p－pq，p－qp，p－pqp，1－qp，q－pq，q－qp，p＋q－pq｝．If one of the elements in the set S is Drazin invertible，then all elements in S are Drazin invertible．

Lemma 2［10］The following statements are equivalent：

1）pq∈RD；

2）1－p－q∈RD；

3）（1－p）（1－q）∈RD．

Lemm a 3［11］（Cline’s formula） Let a，b∈RD．Then（ba）D＝b（（ab）D）2a．

Lemm a 4［1］Let a，b∈RDw ith ab＝ba．Then（ab）D＝bDaD＝aDbD．

Lemma 5［12］Let a，b∈R．If 1－ab∈RDwith ind（1－ab）＝k，then 1－ba∈RDw ith ind（1－ba）＝k and

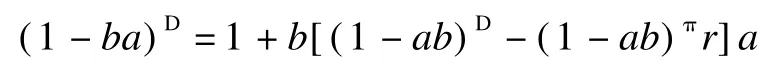
2 M ain Results

In this section，we present some formulae on the Drazin inverse of the difference and the product of idempotents of ring R．

Definition 1 Let p－q∈RD．Define F，G and H as F＝p（p－q）D，G＝（p－q）Dp，and H＝（p－q）D（p－q）．

Theorem 1 Let p－q∈RD．Then F，G and H above are idempotents and

1）F＝（p－q）D（1－q）；

2）G＝（1－q）（p－q）D．

Proof Since p，q are idempotents，we obtain p（pq）2＝（p－q）2p＝p－pqp．Note that a∈RDand ab＝ba imply aDb＝baDby Theorem 1 of Ref．［1］．It follows that p∈comm（（p－q）D）2．Hence，we have

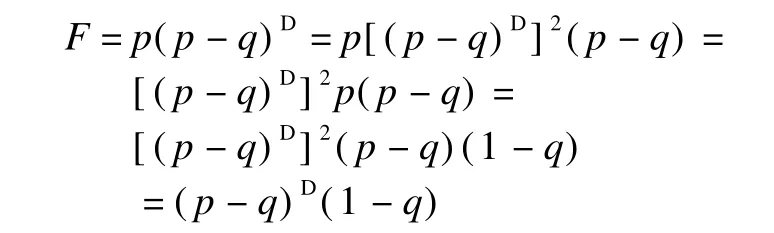
Next，we prove that F is idempotent．From p（p－q）D＝（p－q）D（1－q），we have

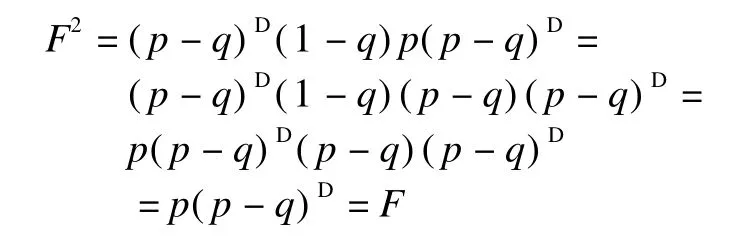
Sim ilarly，G2＝G＝（1－q）（p－q）D．It is clear that H is idempotent and

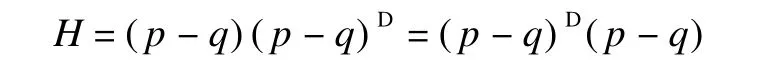
Sim ilarly，we obtain more relationships among F，G and H．

Corollary 1 Let p－q∈RD．Then

1）q（p－q）D＝（p－q）D（1－p）；

2）（p－q）Dq＝（1－p）（p－q）D；

3）qH＝Hq；

4）G（1－q）＝（1－q）F．

Proof 1）and 2）can be obtained by a sim ilar way of Theorem 1．

3）Since H＝（p－q）D（p－q），we have

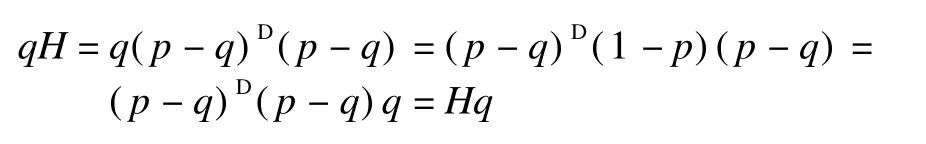
4）By Theorem 1，we have

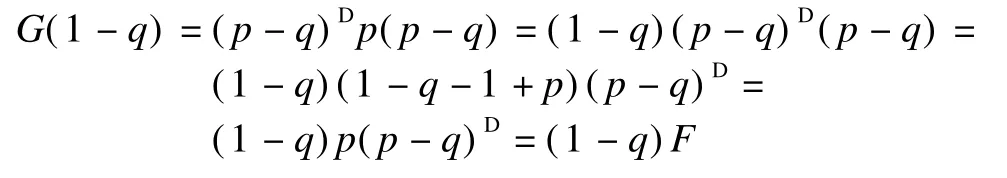
Proposition 1 Let p－q∈RD．Then

1）Fp＝pG＝pH＝Hp；

2）qHq＝qH＝Hq＝HqH．

Proof 1）It is clear that Fp＝pG，we only need to show pG＝pH and pH＝Hp．

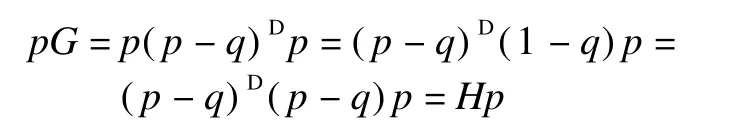
According to Theorem 1，we obtain

Hence，1）holds．

2）Note that qH＝Hq in 3）of Corollary 1．We obtain that qHq＝（Hq）q＝Hq．Since H is idempotent，HqH＝H2q＝Hq．

Thus，qHq＝qH＝Hq＝HqH．

The follow ing theorems，themain results of this paper，give the formulae of the Drazin inverses of the difference and the product of idempotents in a ring R．

Theorem 2 Let p－q∈RD．Then

1）（1－pqp）D＝［（p－q）D］2p＋1－p；

2）（p－pqp）D＝［（p－q）D］2p＝p［（p－q）D］2；

3）（p－pq）D＝p［（p－q）D］3；

4）（p－qp）D＝［（p－q）D］3p；

5）If ind（p－q）＝k，then

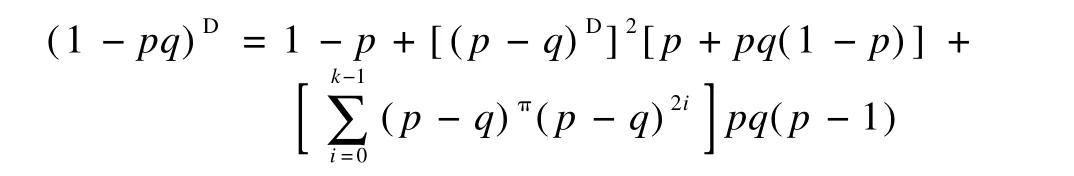
Proof 1）As 1－pqp＝（p－q）2p＋1－p，［（pq）2］D＝［（p－q）D］2and（p－q）2p（1－p）＝（1－p）（pq）2p＝0；then（1－pqp）D＝［（p－q）D］2p＋1－p by Corollary 1 of Ref．［1］．

2）Observing that p－pqp＝p（p－q）2＝（p－q）2p，we obtain（p－pqp）D＝［（p－q）D］2p＝p［（p－q）D］2from Lemma 4．

3）Let x＝p［（p－q）D］3．We prove that x is the Drazin inverse of p－pq by show ing the follow ing conditions hold．

①From p（p－q）2＝（p－q）2p＝（p－pq）p，it follows that

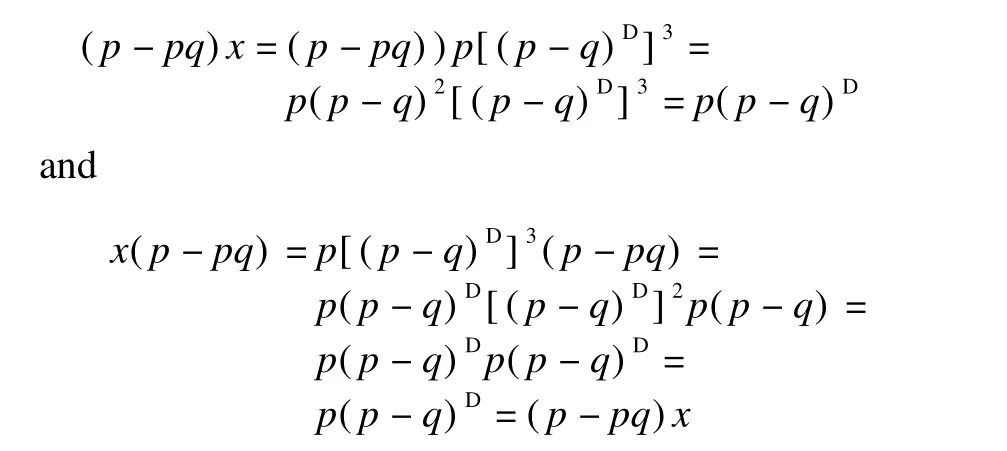
②Note that（p－pq）x＝p（p－q）D．We have

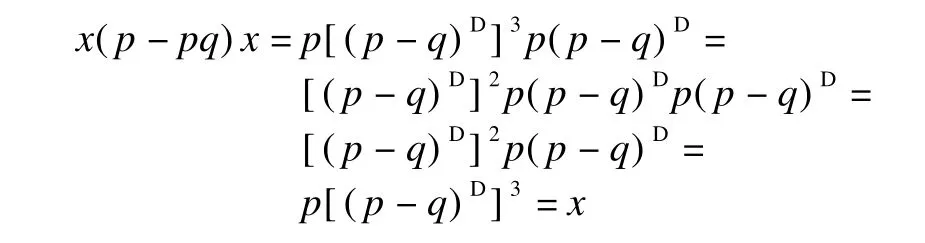
③Since（p－pq）x＝p（p－q）D，we obtain that

According to pH＝Hp and qH＝Hq，it follows that p（p－q）（p－q）π＝（p－q）πp（p－q）．By induction，one can obtain［p（p－q）］m＝p（p－q）2m－1．Take m≥ind（p－q），then［p（p－q）（p－q）π］m＝p（p－q）2m－1（p－q）π＝0．This implies that（p－pq）－（p－pq）2x is nilpotent．

Therefore，（p－pq）D＝p［（p－q）D］3．

4）Use a similar proof of 3）．

5）It follows from Lemma 1 that 1－pq∈RD．Lemma 5 guarantees that

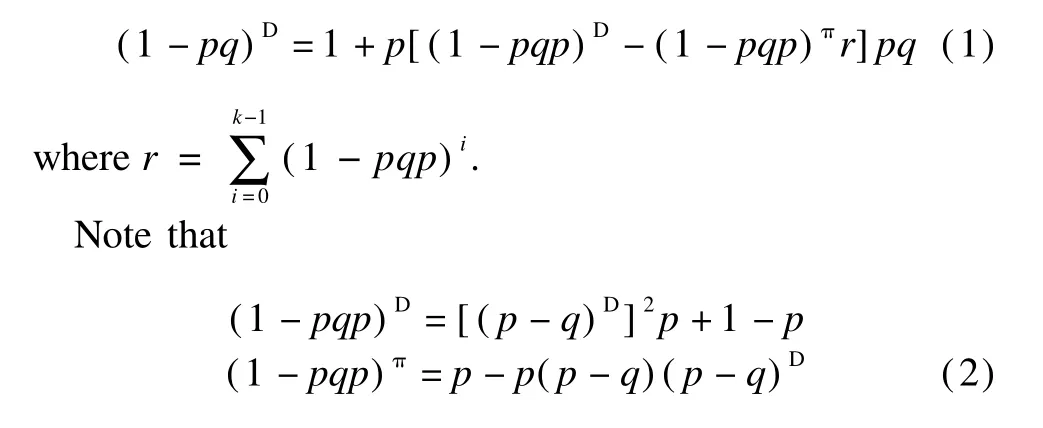
Substituting Eq．（2）into Eq．（1），we have

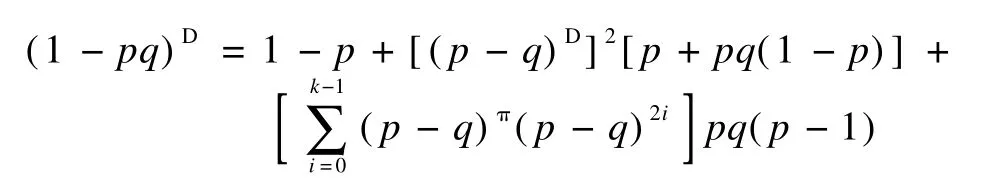
Theorem 3 Let 1－p－q∈RD．Then

1）（pqp）D＝［（1－p－q）D］2p＝p［（1－p－q）D］2；

2）（pq）D＝［（1－p－q）D］4pq．

Proof 1）By pqp＝p（1－p－q）2＝（1－p－q）2p and Lemma 4，it follows that（pqp）D＝［（1－p－q）D］2p＝p［（1－p－q）D］2．

2）From pq＝ppq and Lemma 3，we have（pq）D＝p［（pqp）D］2pq＝［（pqp）D］2pq．According to Eq．（1），we obtain（pq）D＝［（pqp）D］2pq＝［（1－p－q）D］4pq．

Deng［5］and Li［13］considered the following result for projections in Hilbert spaces，C*-algebras，respectively．Indeed，they still hold for idempotents in a ring．

Theorem 4 Let pq∈RD．Then

1）（pq）D＝（pqp）D－p［（1－q）（1－p）］D；

2）（pq）Dpq＝（pqp）Dpq．

Proof 1）By 4）of Theorem 2，we have（p－qp）D＝［（p－q）D］3p and（q－pq）D＝［（q－p）D］3q＝－［（pq）D］3q．

Hence，

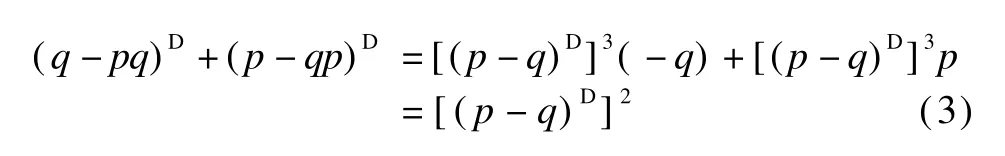
We replace p by 1－p in Eq．（3）to obtain

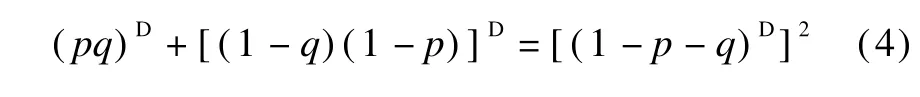
Multiplying Eq．（4）by p on the left yields

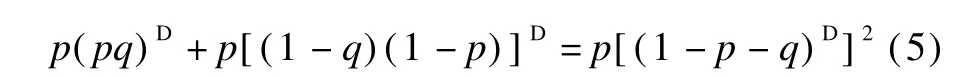
Note that p（pq）D＝p（pq）（pq）D（pq）D＝（pq）Dand Theorem 3．We have

2）By Lemma 3，we have

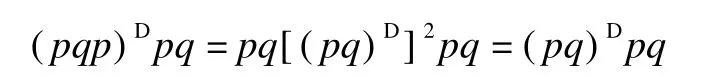
The proof is completed．

Theorem 5 Let1－pq∈RD．Then p－q∈RDand

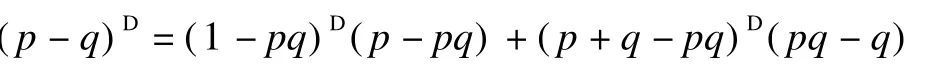
Proof By 5）of Theorem 2，we have

Substituting p and q by 1－p and 1－q，respectively，in Eq．（6），we obtain

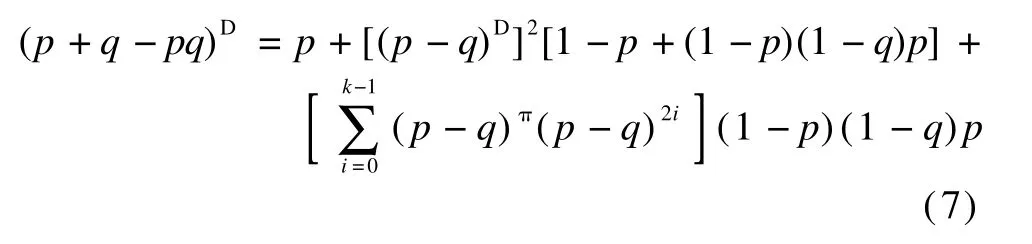
Multiplying Eq．（6）by p－pq on the right yields

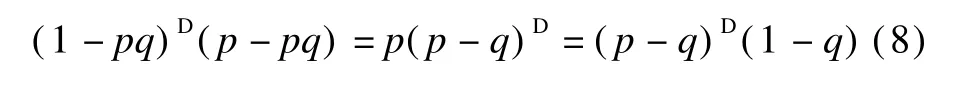
Multiplying Eq．（7）by pq－p on the right yields

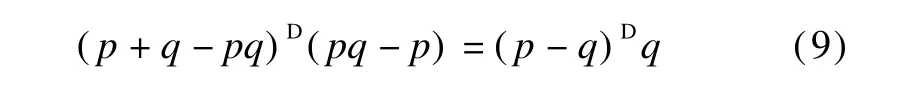
From（8）and（9），one can obtain

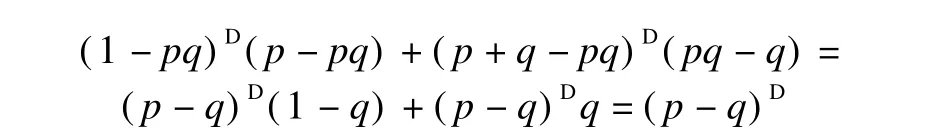
The proof is complete．

Let p，q be two idempotents in a Banach algebra．Then，p＋q∈RDif and only if p－q∈RD．However，in general，this need not be true in a ring．For example，let R＝Z and p＝q＝1．Then p－q＝0∈RD，but p＋q＝2∉RD．Next，we consider what conditions p and q satisfy，and p－q∈RDimplies that p＋q∈RD．

The following result，proved by Deng and Wei［6］for bounded linear operators in Banach spaces，indeed holds in a ring．

Theorem 6 Let p－q∈RD．If F，G and H are given by Definition 1 and（p＋q）（p－q）π∈Rnil，then

1）（p＋q）D＝（p－q）D（p＋q）（p－q）D；

2）（p－q）D＝（p＋q）D（p－q）（p＋q）D；

3）（p－q）π＝（p＋q）π；

4）（p－q）D＝F＋G－H；

5）（p＋q）D＝（2G－H）（F＋G－H）．

Koliha et al．［4］proved that p－q∈R－1implies that p＋q∈R－1for idempotents p and q in a ring R．Hence，we have the follow ing results．

Corollary 2［14］Let p－q∈R－1．If F＝p（p－q）－1and G＝（p－q）－1p，then

1）（p＋q）－1＝（p－q）－1（p＋q）（p－q）－1；

2）（p－q）－1＝（p＋q）－1（p－q）（p＋q）－1；

3）（p－q）－1＝F＋G－1；

4）（p＋q）－1＝（2G－1）（F＋G－1）．

Corollary 3 Let p－qp∈RD，and then（p－q）D＝（p－q）2［（p－qp）D－（q－qp）D］．

Proof Since（p－qp）D＝［（p－q）D］3p and（q－qp）D＝q［（q－p）D］3，we obtain

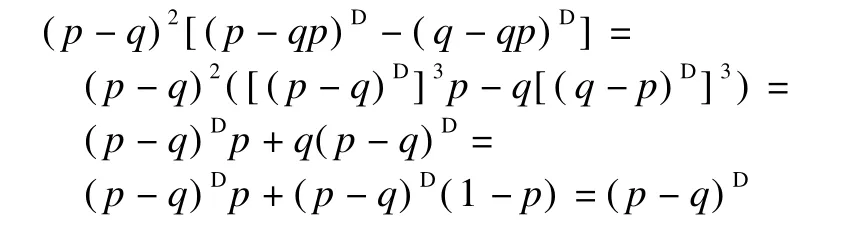
［1］Drazin M P．Pseudo-inverses in associative rings and semigroups［J］．Amer Math Monthly，1958，65（7）：506-514．

［2］GroβJ，Trenkler G．Nonsingularity of difference of two oblique projectors［J］．SIAM JMatrix Anal Appl，1999，21（2）：390- 395．

［3］Koliha J J，Rakocevic V．Invertibility of the difference of idempotents［J］．Linear Multilinear Algebra，2003，50（1）：97- 110．

［4］Koliha JJ，Rakocevic V．Invertibility of the sum of idempotents［J］．Linear Multilinear Algebra，2002，50（4）：285- 292．

［5］Deng C Y．The Drazin inverses of products and differences of orthgonal projections［J］．J Math Anal Appl，2007，355（1）：64- 71．

［6］Deng C Y，Wei Y M．Characterizations and representations of the Drazin inverse involving idempotents［J］．Linear Algebra Appl，2009，431（9）：1526- 1538．

［7］Deng C Y．Characterizations and representations of group inverse involving idempotents［J］．Linear Algebra Appl，2011，434（4）：1067- 1079．

［8］Koliha J J，Cvetkovc-Ilic D S，Deng C Y．Generalized Drazin invertibility of combinations of idempotents［J］．Linear Algebra Appl，2012，437（9）：2317- 2324．

［9］Zhang S F，Wu J D．The Drazin inverse of the linear combinations of two idempotents in the Banach algebra［J］．Linear Algebra Appl，2012，436（9）：3132- 3138．

［10］Chen J L，Zhu H H．Drazin invertibility of product and difference of idempotents in a ring［J］．Filomat，2014，28（6）：1133- 1137．

［11］Cline R E，An application of the representation for the generalized inverse of a matrix［J］．MRC Technical Report，1965．

［12］Castro-Gonzalez N，Mendes-Araujo C，Patricio P．Generalized inverses of a sum in rings［J］．Bull AustMath Soc，2010，82（1）：156- 164．

［13］Li Y．The Drazin inverses of products and differences of projections in a C*-algebra［J］．JAustMath Soc，2009，86（2）：189- 198．

［14］Koliha J J，Rakocevic V，Straskraba I．The difference and sum of projectors［J］．Linear Algebra Appl，2004，388：279- 288．

环中涉及幂等元的Drazin逆的表示

朱辉辉 陈建龙

（东南大学数学系，南京211189）

称环R中的元素a为Drazin可逆的，如果存在R中的元素b使得ab＝ba，bab＝b，a－a2b是幂零的．上述元素b如果存在则是唯一的，并表示为aD．给出了一些环中涉及幂等元的Drazin逆的等价条件．作为应用，给出了环中幂等元的积与差的Drazin逆的公式．因此，一些关于Banach空间中有界线性算子的结果被推广到环上．

幂等元；Drazin逆；谱幂等元

O151．2

10．3969／j．issn．1003－7985．2015．03．023

2013-10-14．

Biographies：Zhu Huihui（1985—），male，graduate；Chen Jianlong（corresponding author），male，doctor，professor，jlchen＠seu．edu．cn．

s：The National Natural Science Foundation of China（No．11371089），the Specialized Research Fund for the Doctoral Program of Higher Education（No．20120092110020），the Scientific Innovation Research of College Graduates in Jiangsu Province（No．CXLX13-072），the Scientific Research Foundation of Graduate School of Southeast University，the Fundamental Research Funds for the Central Universities（No．22420135011）．

：Zhu Huihui，Chen Jianlong．Representations of the Drazin inverse involving idempotents in a ring［J］．Journal of Southeast University（English Edition），2015，31（3）：427- 430．

10．3969／j．issn．1003－7985．2015．03．023