基于模糊相似优先比法的灌区降雨典型水文年选取研究
褚桂红,史文娟
(1山西省水利水电科学研究院 山西太原 030002;2西安理工大学西北水资源与环境生态教育部重点实验室 陕西西安 710048)
典型年的选择原则是年内总量及年内分配过程都具有代表性。早期典型年的选取均采用频率分析法,因个人经验不同,选取的典型年一般都会出现因人而异的情况,因此,在选取典型年的过程中应既考虑年内总量又兼顾年内分配情况,同时减少人为因素的影响,从而使得所选择的典型年更具代表性。对灌区降雨典型年选取而言,由于研究对象的模糊性,且年降雨量中丰水年、平水年和枯水年之分等没有明确的分界点,因此运用模糊数学方法进行研究较为恰当[1]。特别是目前随着科学技术的飞速发展,数据挖掘技术进入了一个新阶段,各种聚类方法及模糊分析方法在水资源系统优化决策及其他领域都得到了广泛的应用[2-5],但这些研究多集中在水沙年代表性的选取上,而对典型水文年的研究并不多见,且在水沙典型年的选取研究中或只考虑了水沙总量,对年内过程未予讨论;或通过年内过程的分析,给出了一组具有一定代表性的水沙年,但如何判断年内过程分配的优劣,仍然需要借助经验加以确定。因此,在选取典型水文年年的过程中既考虑年内总量又兼顾年内分配情况,同时减少人为因素的影响,从而使得所选择的典型年更具代表性是本文研究的重点。
1 系统聚类法
1.1 系统聚类算法及步骤
聚类分析是数据挖掘的一项重要功能,而聚类算法是目前研究的核心,其基本思想是:设有n个样本,每个样本有m项指标。首先定义样本间的距离,然后将距离最近的两类合并为新类,并计算新类与其他类的距离,再按最小距离准则并类,以此类推,直至并为一类为止。这种系统归类过程与所规定的归类指数有关,同时也与具体的归类方法有关系,整个聚类过程可用一张聚类图形象表示[6]。聚类增强了人们对客观现实的认识,是概念描述和偏差分析的先决条件。聚类技术主要包括传统的模式识别方法和数学分类学。通过模型的建立和规则的制定,对一个给定的数据集进行划分,并最大化类间的相似性,最小化类内的差别性,从而形成聚类,其步骤如下:
(1)规定对象间的距离,计算样本距离,本文采用欧式距离;
(2)规定类与类之间的距离,计算类间距离。因类平均法既是空间守恒又具有单调的性能[7-8],本文采用平均距离法;
(3)计算新类与其它类的距离;
(4)重复(2)、(3)步骤,直至合并为一类;
(5)确定聚类树上分类的位置,形成聚类结果。
1.2 灌区降雨聚类分析
灌区降雨量的大小及时空分配特征主要受控于流域水文气象、自然地理、地形地貌等确定因素,但同时又具有随机性和模糊性,为确定灌区降雨丰水年(P=25%)、平水年(P=50%)和枯水年(P=75%)的典型年,本文采用系统聚类算法对涝河灌区1959-2002年共43年(缺1977年)降雨资料进行划分。为突出灌区的特点和主要矛盾,选取年降雨总量及灌区内主要种植作物冬小麦、夏玉米、棉花主要生育期降雨量及枯水期降雨量五个影响指标进行分析。
利用MATLAB中的聚类统计工具对灌区1959-2002年的实测降雨量进行聚类,划分出丰水年组、平水年组和枯水年组,结果见表1。
2 典型年选取
2.1 模糊优先比法
选定固定样本U(U={u1,u2,u3…,un}),其特定目标样本为Uk(1≤k≤n)。模糊相似优先比法就是在其余n-1个样本中,选出哪些样本与特定目标样本uk最相似,哪些样本次之。该过程是将样本集合中U每一对元素ui、uj与特定目标样本uk相比较,建立任意元素间的相似比关系rij,rij极值有以下3种情况:
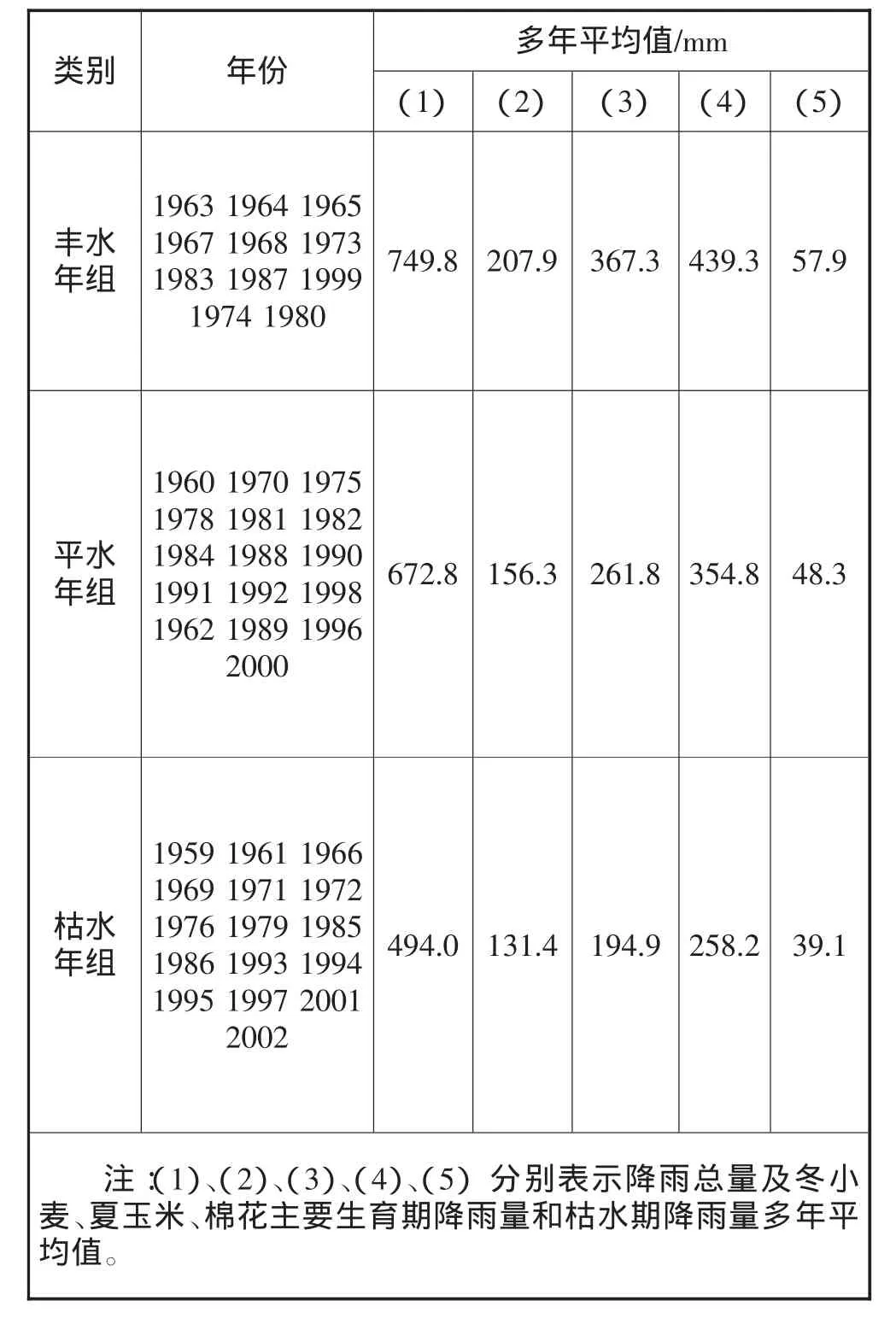
表1 降雨聚类结果
如果rij=1(i,j=1,2,……,n),表示ui绝对比uj优先;
如果ri j=0.5(i,j=1,2,……,n),表示ui与uj等价;
如果rij=0(i,j=1,2,……,n),表示uj绝对比ui优先;
并且rij具有如下特征:
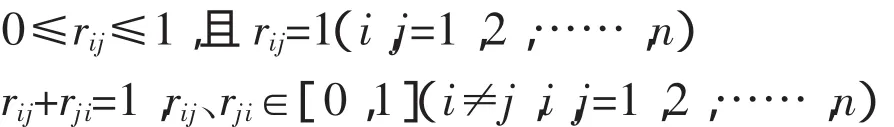
在确定rij时,一般采用绝对值距离:
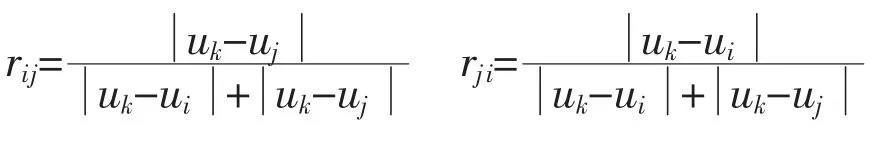
利用λ(0≤λ≤1)的截距对U中各元素进行排序。根据rij值由大到小选取λ的截矩阵Rλ。
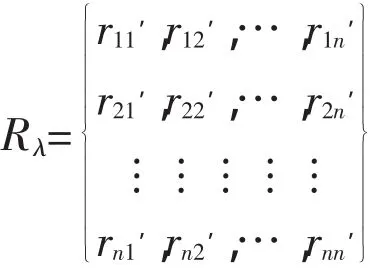
2.2 灌区降雨典型年的确定
样本集合为涝河灌区1959-2002年共43年(缺1977年)的实测降雨资料,目标样本为聚类后各水平年组的总降雨量多年平均值及灌区主要种植作物冬小麦、夏玉米和棉花主要生育期降雨量平均值和枯水期降雨量平均值5个因子。下面以平水年组总降雨量多年平均值为例,计算得到平水年组总降雨量的优先比矩阵:
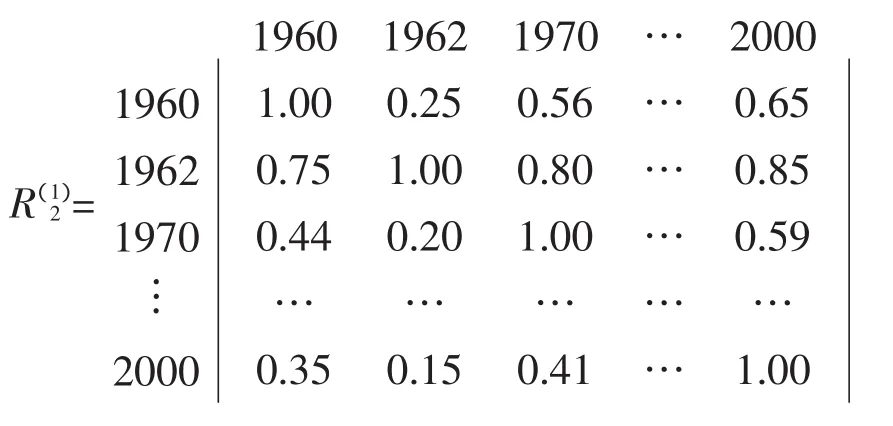
令λ依次由大到小截得Rλ,并进行降序排列。典型年的选取,就是确定各年各评价因素与多年平均最接近的一年,即该年份就可以作为典型年。本文所选取的5个评价因子中,认为各评价因子对典型年选取同等重要,其权重取值均为0.2。各影响因子优先相似顺序及评价最终结果见表2、表3和表4。
根据计算结果,其综合值越小,表示相似度越高。因此丰水年影响因子综合值最小的年份为1965年,故选择丰水典型年为1965年最好,1963年次之,类似于上述选取典型年的方法可知平水典型年为1982年最好,1970年次之,枯水典型年为1979年最好,1969年次之。综合考虑各分类典型年选取结果见表5。
将运用模糊相似优先比法选取的典型年与频率分析法的计算结果相比较(见表5),从表5可知:模糊相似优先比法与频率法的计算结果既有吻合,但又存在明显的区别,产生这种差别的原因是研究对象的模糊性所致。在典型年的选取过程中,频率分析法仅考虑了年内总量,未考虑年内分配,如典型平水年用频率分析法选择2000年作为典型年,而模糊相似优先比法则为1982年,从年均总量上看2000年的降水量最接近多年平均值,但降水年内分配上1982年较2000年更为不利,故选择1982年为典型平水年更具代表性。由此可以看出应用模糊相似优先比法选取的典型年更符合实际情况,且该方法又明显优于传统的频率分析法。

表2 丰水年组实测降雨过程优先相似序列

表3 平水年组实测降雨过程优先相似序列
3 结论与讨论
(1)模糊相似优先比法是以数理统计与模糊聚类分析相结合的方法,可以消除因个人经验的不同而确定典型年的任意性,使典型年过程的推求建立在严格的数学模型基础上,该方法不仅考虑了降雨总量,而且还考虑了降雨量的年内分配情况,因此,选出的典型水文年更具有代表性。
(2)应用模糊相似优先比法选取典型年,其结果避免了人为经验带来的主观性和片面性,选取的典型年更符合实际情况,且该方法明显优于传统的频率分析法。
(3)结果的可靠性取决于选择相似因子的合理性,若能根据各因子的重要程度确定合理的权重,其结果将更符合实际。

表4 枯水年组实测降雨过程优先相似序列
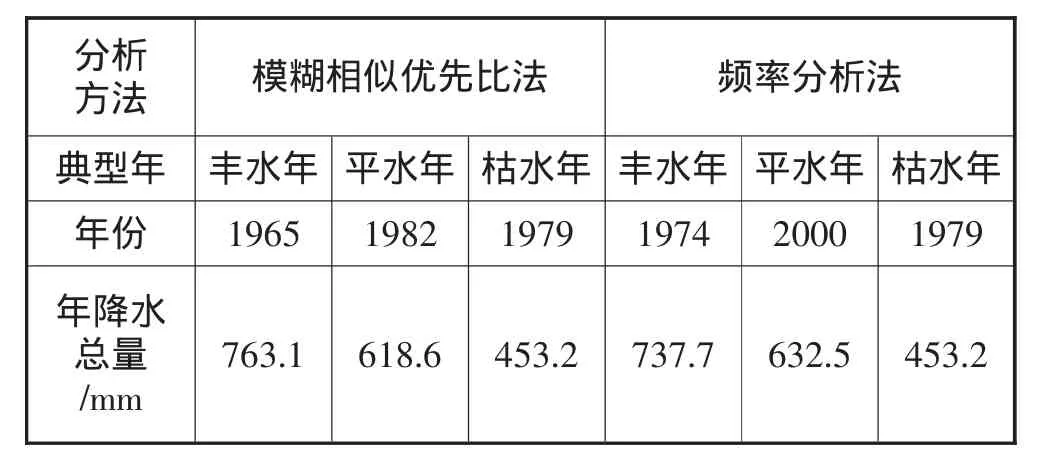
表5 各分类典型水文年计算结果
[1]夏莉敏,张 玮.基于模糊聚类迭代模型的典型水文年选取研究[J].武汉理工大学学报(交通科学与工程版),2009,33(4):695-698.
[2]张跟广.选择典型水沙年的一种新方法——模糊相似优先比法[J].陕西水力发电,1994(1):17-22.
[3]于雪峰,陈守煜.模糊聚类迭代模型在洪水灾害度划分中应用[J].大连理工大学学报,2005,45(1):128-131.
[4]李亚伟,陈守煜,傅铁.基于模糊识别的水资源承载能力综合评价[J].水科学进展,2005,16(5):726-729.
[5]奥 勇.模糊聚类迭代模型在环境评价分区研究中的应用[J].西安科技大学学报,2007,(2):244-246.
[6]刘国华,钱镜林,汪树玉.产汇流模型参数综合率定在洪水预报中的应用[J].浙江大学学报(工学版),2003,37(5):576-581.
[7]柳 卓,曹飞凤,杜光潮.系统聚类方法在洪水预报中的应用研究[J].浙江水利科技,2008,159(5):1-3.
[8]柳 卓.系统聚类方法在洪水预报中的应用研究[D].浙江:浙江大学,2007.

