塔机弓板力矩限制器灵敏度改进算法研究
李 力 曾德学
(三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002)
随着我国城市化建设进程的加快,塔式起重机(以下简称塔机)的保有量持续攀升,与此同时,塔机重大伤害事故的发生率也居高不下[1],塔机事故发生率从1999年的3.9‰增加到2011年的22.7‰[2-3],根据江苏省2005年至2009年统计的数据,超载是引发塔机事故的主要原因[4].
力矩限制器作为塔机必备的也是最有效的重要安全保护装置,被广泛用于防止塔机因超载及起重力矩过大而引起的倒塔事故.力矩限制器一般分为机械式和电子式,其中机械式包括偏心拉杆式和弓板式,由于弓板式力矩限制器结构简单、成本低、维修方便,因此大多数塔机使用弓板式力矩限制器.现行的弓板式力矩限制器普遍存在精度不高、灵敏度偏低的问题.一般要求其弓板力矩限制器的挠度变化量在20~30mm,以便有足够的调节灵敏度,但很多弓板放大后的挠度变化量只有4~5mm,灵敏度及重复性都不好[5],放大率计算不准确是导致其设计行程达不到要求的主要原因.
文献[6]提及采用悬臂梁模型计算的方法得到弓板力矩限制器的放大率为675倍,采用虚功原理计算出的放大率为45倍,计算结果偏大;文献[7]通过ANSYS有限元仿真法计算出的放大率约为5.37,针对不同尺寸弓板力矩限制器须分别建模,计算步骤繁琐;文献[8]通过ANSYS有限元仿真对不同结构的弓板力矩限制器结构参数采用控制变量法仿真,得到放大率在5~35之间,并指出当放大率不小于8时可满足使用要求,同样需要针对不同型号及尺寸的弓板力矩限制器分别建模进行计算.这些文献大多仅从弓板力矩限制器自身的结构参数出发计算放大率,并未考虑实际情况下塔机在特性曲线规定的范围内起吊重物时弓板力矩限制器放大率能否达到设计的要求.
针对以上问题,本文采用解析法对放大率进行改进计算.首先根据定义得出放大率方程,然后通过力学分析法对弓板力矩限制器、塔顶、平衡臂、起重臂分别进行受力分析,层层递进推导出放大率方程表达式中各参数的解析式,最后应用Matlab软件对放大率解析式进行仿真.
1 弓板力矩限制器结构及原理
弓板力矩限制器是一个变形放大器,作为一种物理量传感器,需要足够的灵敏度才能起到应有的作用.以下将从结构、工作原理以及影响灵敏度因素等方面论述弓板力矩限制器.
1.1 弓板力矩限制器结构
弓板力矩限制器由弓形钢板、限位开关、调节螺杆、支撑杆等构成,如图1所示.两块弓形钢板2成弧形结构拼接,弓形钢板的两端均焊接在塔顶主弦杆1上,调节螺杆5以及限位开关4安装在弓形钢板的中部.当塔机起吊重物时,主弦杆1在力的作用下产生压缩变形,弓形钢板随着主弦杆1的变形而发生形变并在弓形钢板的作用下加以放大,带动调节螺杆5和限位开关4,当起重力矩达到设定极限值时调节螺杆5触动限位开关4起到保护作用,其工作的主要原理是将不容易测量的起重力矩转变为便于测量的弓形钢板水平方向的位移.

图1 弓板力矩限制器结构示意图
1.2 灵敏度影响因素
弓形板力矩限制器作为一个变形放大器,必须有较好的灵敏度才能够起到力矩保护作用.灵敏度是指某方法对单位浓度或单位量待测物质变化所致的响应量变化程度,它可以用仪器的响应量或其他指示量与对应的待测物质的浓度或量之比来描述,针对塔机弓形板力矩限制器,灵敏度体现在挠度变化量上.现行多数弓板力矩限制器挠度变化量并不满足20~30 mm的使用要求,因此灵敏度是不准确的.
弓板力矩限制器的挠度是指受力变化时,弓板力矩限制器的单片弓板中性层在垂直于两片弓板对称轴线方向的线位移.挠度变化量越大,灵敏度越好.而挠度变化量的大小受到弓板力矩限制器放大率的影响.在力的作用下,放大率越大,如果挠度变化量越大,则相应的弓板力矩限制器灵敏度高,反之则相反.
弓板力矩限制器放大率定义为弓高变化量与弓长变化量之比,放大率越大,弓板的放大效能也越好.弓板力矩限制器的弓长、弓高、厚度、初始挠度、材质以及曲率的均匀性和塔机的结构参数、特性曲线等均会对放大率产生影响.放大率过小直接导致挠度变化量不足,从而使得灵敏度不准确.
本文对现行弓板力矩限制器放大率算法做一改进,不仅考虑到原有算法中弓板力矩限制器自身结构参数的影响,还额外考虑到塔机的特性曲线、结构参数等对放大率的影响,因此计算较为准确.
2 改进算法
改进算法是在考虑弓板自身结构参数以及塔机的结构参数以及特性曲线等因素的基础上,主要通过力学分析法推导放大率及挠度的具体解析式.
2.1 放大率分析与计算
由于弓板力矩限制器是对称结构,受力分析时考虑其中的一片即可,单片弓板受力分析示意图如图2所示.
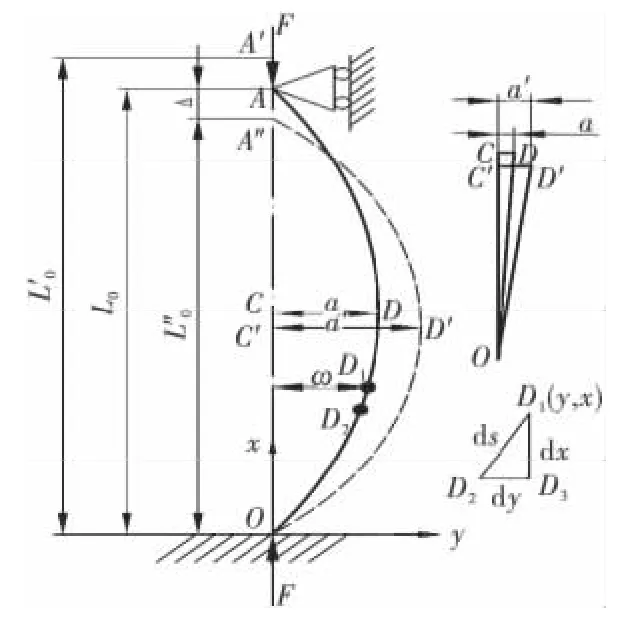
图2 单片弓板受力分析示意图
记弓板力矩限制器的放大率为k,则其计算公式如下:

式中,k为弓板力矩限制器的放大率,Δa′为塔机工作时弓高变化量,Δ为塔机工作时的弓长变化量.
为计算公式(1)的具体解析式,需计算出a′与的表达式.如图2取微弧段D1D2,其弦长ds与其在x轴方向的投影之差即为该微弧段弓板D1D2弯曲后在x轴方向的变形量:

式中,ds为微弧段D1D2的弦长,dx为微弧段D1D2在x轴方向的投影长度,y′为挠曲线方程求导.
对公式(2)进行幂级数展开,并取x在全长范围内积分,求出弓板在x轴方向总的变形量为:

式中,Δ是塔机工作时弓板在x轴方向总的变形量,该变形量由两部分引起:第一部分是由于压力F引起塔机主弦杆变形造成的在x轴方向的支座位移量Δ1,第二部分是弓板初弯曲后自身的弯曲变形量Δ2.由胡克定律及中心压杆的变形规律可知,主弦杆变形造成的支座位移变形量Δ1及弓板的弯曲变形量Δ2分别为:

显然有Δ=Δ1+Δ2,代入公式(3)、(4)、(5),得到弓板力矩限制器上最大变形量为:

弓板力矩限制器工作时弓长的表达式如下:

联立公式(6)和公式(7)得到弓板力矩限制器工作时弓长和弓高a′的解.根据放大率的定义和公式(1),计算出弓板力矩限制器放大率解析式为:
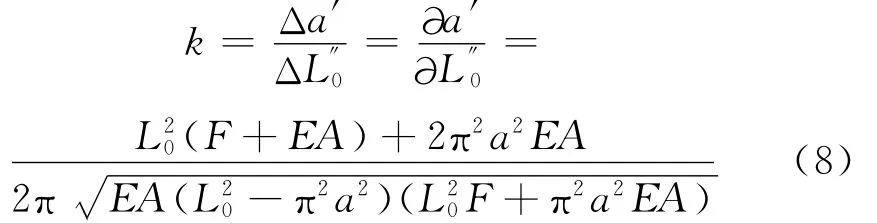
由公式(8)可知,弓板力矩限制器初始的弓高a以及弓长L0是直接影响其放大率的主要因素,放大率还与安装弓板力矩限制器所在的塔顶主弦杆的弹性模量E以及横截面积A有关,另外主弦杆所受内力F也是影响弓板力矩限制器放大率的关键因素之一.
2.2 挠度分析与计算
为计算放大率与挠度变化量之间的关系,需推导挠度的解析式.结合图2,在钢板的弹性范围内,弓板的变形满足胡克定律,求得该正弦型弓板力矩限制器上任意一点的挠度ω满足挠曲线方程:

式中,ω为弓板力矩限制器上任意一点的挠度,a′为弓高为弓长,x为弓板上任意一点的纵坐标.
将公式(6)代入式(9),并考虑到是变量,不方便实时测量,塔机主弦杆的轴向变形十分微小,近似取=L0,则挠度解析式简化为:

一旦塔机型号确定,并选定弓板力矩限制器,由公式(9)和(10)可知,放大率和挠度的大小仅取决于塔机起吊过程中弓板力矩限制器所在主弦杆所受力F的大小.
2.2.1 主弦杆内力与拉杆拉力关系的计算
对塔顶进行的受力分析如图3所示,取弓板力矩限制器安装所在塔顶主弦杆所在位置截面Ⅰ-Ⅰ为分析主弦杆内力的截面,根据力的平衡原理和力矩平衡原理对A2点取矩有:

式中,hi为A2点与拉杆i之间距离,i=1,2,3,分别与拉力Fi中的i对应,h4为A2点与A4点之间距离,L7为A3点与B3点之间的距离,其余符号意义见图3.
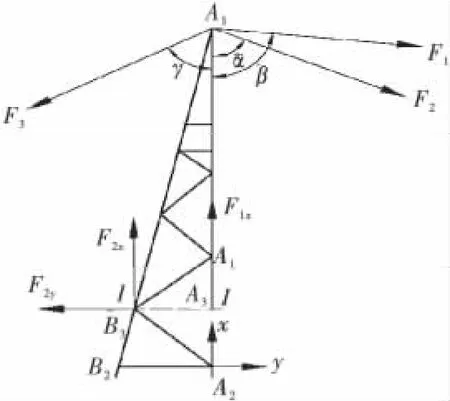
图3 塔顶受力分析
安装弓板力矩限制器的塔顶主弦杆所受轴力等于塔顶主弦杆内力,即F1x=F,由方程组(11)解方程,得到主弦杆内力F与拉杆拉力F1,F2,F3的关系如下:
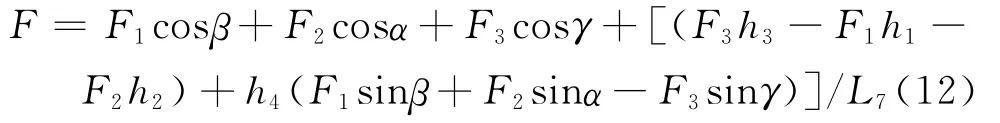
2.2.2 拉杆拉力与配重、吊重、幅度关系的计算
对塔机平衡臂进行受力分析如图4所示,平衡配重G作为集中力加载,考虑平衡臂自重较大,结构比较均匀,故将平衡臂的自重作为均布荷载分布在整个平衡臂上,根据力的平衡原理和力矩平衡原理对B4点取矩有:


图4 平衡臂受力分析
作为作用力与反作用力,F3=,解方程组(13)得平衡臂拉杆的拉力为:

对起重臂进行受力分析如图5所示,双吊点动臂式塔机的起重臂架是一次超静定结构,要求出拉杆拉力,必须对起重臂的结构进行简化.图5将拉杆A1C3以多余约束力代替,则起重臂架简化为静定的基本结构.由于起重臂自重较大,结构比较均匀,也将起重臂的自重作为均布荷载分布在整个起重臂上,起重臂的截面惯性矩不变.

图5 起重臂受力分析
根据力的平衡原理和根据力矩平衡原理,对A4点取矩有:
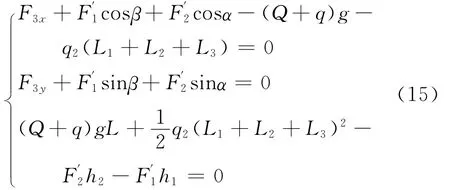

根据位移变形条件得出变形协调方程:

式中,δ11为单位载荷单独作用下拉杆A1C3截断点沿着方向的位移,Δ1P为在臂架自重载荷q2、吊重Q及吊具重q作用下拉杆A1C3截断点沿着方向的位移,其余参数如图所示.
解变形协调方程时,分别在=1单独作用于起重臂以及吊重Q+q与均布载荷q2共同作用于起重臂两种情况下对起重臂进行受力分析,吊重处于内吊点之内、两吊点之间以及外吊点之外时,要分别进行计算讨论,得出的解δ11为定值,此处不再赘述.
吊点不同时,得到的Δ1P的表达式不同,且表达式比较复杂.考虑到塔机在运行过程中幅度L在不断变化,不同情况下Δ1P的解可归结为如下形式:

式中,Ai(i=0,1,2,3,4)均为常数,吊重分别处于内吊点之内、两吊点之间以及外吊点之外时Δ1P的表达式有所不同,体现为Ai(i=0,1,2,3,4)的值有所差异.
3 数值仿真分析
选取型号为QTZ160双吊点动臂自升式塔机为例,取其结构尺寸,并选定现行常用弓板力矩限制器结构参数如图1中所示,对上述计算的挠度与放大率进行仿真.当塔机在特性曲线限定的起重量起吊重物时,计算弓板力矩限制器的放大率及挠度变化量,看其放大率是否不小于8,挠度变化量是否在20~30 mm,并根据计算结果给出调整建议.
当起重力矩从0到额定起重力矩变化时,得到的挠度变化量仿真结果如图6所示.根据计算的挠度与放大率解析式,当塔机在特性曲线限定的起重量起吊重物时,弓形板力矩限制器实际放大率为1.82,并不满足放大率不小于8的使用要求,对应的挠度变化量也不在20~30mm的变化范围内,仅仅接近8mm.因此,该弓板力矩限制器结构参数与所选型号塔机并不匹配,需对弓板力矩限制器的结构参数进行更改.

图6 单片弓板挠度变化量随起重力矩变化图
弓形板力矩限制器是非标设备,一般采用厚度为5~10mm,宽40~60mm的合金结构钢板制造(一般选择材料为Q235-A),一般情况下其弓高为20~40 mm,弓长为1 000~1 500mm[8],即公式(8)中的a=[20,40],L0=[1 000,1 500],根据公式(8)结合这些参数的范围对弓板力矩限制器的放大率k与弓高a及弓长L0的变化情况进行仿真.从仿真结果来看,在限定的范围内,弓高a取极小值而弓长L0取极大值时放大率k的值最大.要满足放大率达到8的使用要求,在减小弓高增大弓长的同时,还可采取减小塔顶的刚度、选择弓板力矩限制器敏感的安装位置等措施.
与以往的算法对比,该算法不仅考虑了弓板力矩限制器自身结构参数,还考虑了塔机结构参数对弓板力矩限制器的影响.仅仅考虑弓板力矩限制器自身结构参数计算的放大率只是理论放大率,并不能保证起吊塔机特性曲线限定的起重量时能够达到计算的放大率,因此这种计算方式是不适用的.改进后的算法考虑到塔机的结构参数、特性曲线等对放大率造成的影响,计算的解析式具有普遍性,与实际测量的结果一致.给定塔机型号以及弓板力矩限制器结构参数,就可以根据推导的解析公式计算该弓板力矩限制器安装于塔机上时其放大率是否满足不小于8的使用要求,以及挠度变化量是否在规定的20~30mm范围内变动.这对于弓板力矩限制器的设计及选型具有理论与实际应用价值.
4 结 论
本文推导塔机弓形板力矩限制器的具体解析式并采用Matlab软件进行仿真,得到的结论如下:
1)现行弓板力矩限制器灵敏度不准的原因是挠度变化量不满足使用要求,具体的表现是放大率计算不准确,在塔机型号给定的情况下,减小弓板力矩限制器的弓高并增大其弓长可提高放大率.
2)对弓板力矩限制器进行设计计算时,不仅要考虑弓板力矩限制器自身结构参数的影响,还要考虑到塔机的结构参数、特性曲线等因素,否则计算的放大率并不适用.
3)根据计算的解析式,提高弓板力矩限制器放大率还可采取减小塔顶刚度、将弓板力矩限制器安装于塔顶后主肢受力敏感位置等措施.
此外,本文计算的放大率及挠度解析式可普遍应用于双吊点动臂自升式塔机,对于不同型号的塔机与不同结构参数的弓板力矩限制器,只需改变解析式中对应参数的值即可计算出弓板力矩限制器是否满足使用要求,对设计弓板力矩限制器及提高其放大率以增加其灵敏度具有理论与应用价值.
[1] 邓亮华,张 优.塔式起重机安全监控系统的研究与应用[J].建设机械技术与管理,2011(4):92-94.
[2] 李 丽,牛秀艳,赵 爽,等.塔式起重机事故分析与对策[J].吉林建筑工程学院学报,2007,24(1):67-70.
[3] 鞠 晖.塔式起重机常见事故分析及安全监督管理[J].建筑安全,2005(3):44-45.
[4] 潘 亮,张作萍,陈文亮.塔式起重机安全监控装置的研究现状[J].建筑安全,2013(1):64-65.
[5] 张大志.塔式起重机力矩限制器调试[J].建筑机械,2003(4):55-57.
[6] 邹力生.弓式力矩限制器的变位分析[J].建筑机械化,1989(2):27-28.
[7] 王兴杰,朱 斌.基于ANSYS的塔机力矩限制器变形比例的分析计算[J].建筑机械化,2011(增刊2):115-116.
[8] 文朝辉.塔式起重机弓板力矩限制器设计分析[J].建筑机械化,2014(2):79-82.

