脉动风载环境下发射天线结构时程响应分析

方子帆 覃 涛 朱 陈 陈智会 槐以良

（1.三峡大学 机械与动力学院，湖北 宜昌 443002；2.三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002；3.湖北中南鹏力海洋探测系统工程有限公司，湖北 宜昌 443005）

高耸塔架属于高度较高且横向刚度较小的结构，侧向载荷作用下会产生较大的结构反应，风载荷往往是塔架的主要影响载荷.作用在塔架结构上的风载荷主要包括顺风向的平均风、脉动风和横风向的涡流干扰［1］.平均风载荷对于结构的作用相当于结构静力载荷；脉动风的周期较短，较接近塔架结构的自振周期，从而会在结构的顺风方向引起振动，此形式的振动需要在实际工程结构计算分析中予以考虑，即塔架结构的风振响应分析.国内外已做了大量关于脉动风的研究，例如温德超［2］等人对某80m的烟囱从其固有频率、风振频率和雷诺数2方面研究了该烟囱的振动问题.

常用脉动风的风速谱有Davenport谱、Kaimal谱、Hino谱等［3］，我国规范及风工程针对高耸结构应用中一般采用Davenport谱［4］，而Davenport谱是以10m高度处风速为基准风速，且风速谱不随高度变化，而本文采用基于线性滤波器法的自回归模型（AR模型）针对Davenport谱进行了风速模拟，AR模型模拟的风速谱随高度变化而变化，基于Matlab编程得到AR模型，并求出风压载荷谱，进而进行发射天线结构的结构动力学分析.

本文利用有限元软件WorkBench建立发射天线结构有限元模型，考虑结构中各节点脉动风的空间相关性，分析了结构顺风向的脉动风引起的结构振动，采用AR法模拟结构顺风向各节点的脉动风载时程，分析发射天线结构的动力特性，同时对天线地基进行了抗倾覆分析（本文由于结构横截面较小，故不考虑横风向的涡流对结构的影响）.

1 风的基本特性及风载荷计算

1.1 平均风速

平均风是给定时间内，风力大小、方向等不随时间改变的量，随高度变化改变而改变，表达式为

式中，z、vs为任意点高度及该处的平均风速；z1，v1为标准高度（10m）及该处的平均风速；α是与地面粗糙度有关的指数.

1.2 脉动风速谱

顺风湍流风速分量u的频率分布可通过无量纲功率谱密度函数RN（z，ω）来表示

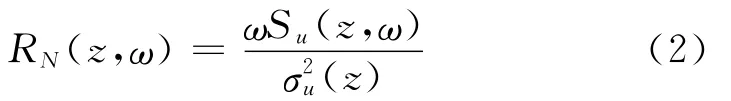
式中，ω为圆频率；Su（z，ω）为顺风向湍流分量的功率谱；σu（z）为高度z处湍流分量u的标准方差.

风工程中普遍采用的风谱函数的研究基础多是Kolmogrove假设推论给出的纵向脉动风载功率谱的一般表达式，即

式中，u0为剪切波速；x为相似律坐标；A，B为常数；α，β，γ为谱的幂指数，满足γ－αβ＝2／3.

根据我国规范［5］及在风工程应用中一般采用Davenport谱.其表达式为

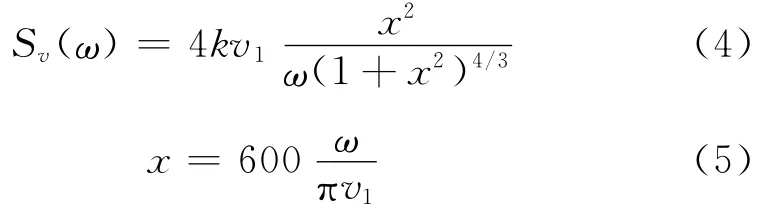
式中，Sv（ω）为脉动风速功率谱；k为反映地面粗糙度的系数；ω为圆频率.

1.3 脉动风的互功率谱及空间相关性

对于迎风面尺度较大的结构要考虑脉动风的空间相关性，对于任意相距r的两点i，j，其纵向脉动风速的交叉谱［6］可表示为

式中，（ω）、（ω）分别为i，j两点的风速谱；Coh（r，ω）为相关函数的平方根，也称为相关函数.

目前相关系数常用单位是Davenport给出的经验公式.

在高度方向：

在水平方向：

1.4 自回归模型（AR）模拟脉动风速时程

时间序列模型是描述时间序列统计特性的一种常用方法，数学上用随机差分方程来表示时间序列模型的结构，在时域上的解就是时间序列的自相关特性.

M个点空间相关脉动风速时程V（X，Y，Z，t）列向量的AR模型可以表示为

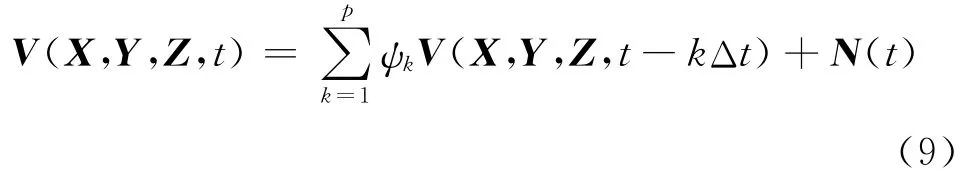
式中，X，Y，Z均为坐标向量矩阵，（xi，yi，zi）为空间第i点坐标，i＝1，2，…，M；p为AR模型阶数，ψk为AR模型自回归系数矩阵，k＝1，…，p；Δt是模拟风速时程的时间步长；N（t）＝Ln（t），n（t）为（0，1）的彼此独立的正态随机过程，L为M阶下三角矩阵.

考虑相关函数性质，可以得到协方差矩阵R与回归系数ψ的关系：

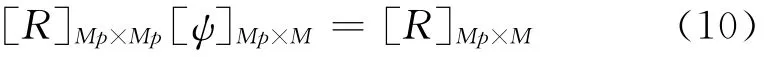
通过以上各式，可以求出自回归系数矩阵［ψ］，并进一步求得矩阵RN：

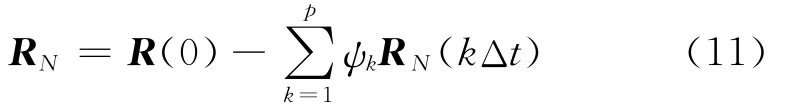
求得系数矩阵［ψ］和矩阵RN后，求最终M个相关的随机风过程：

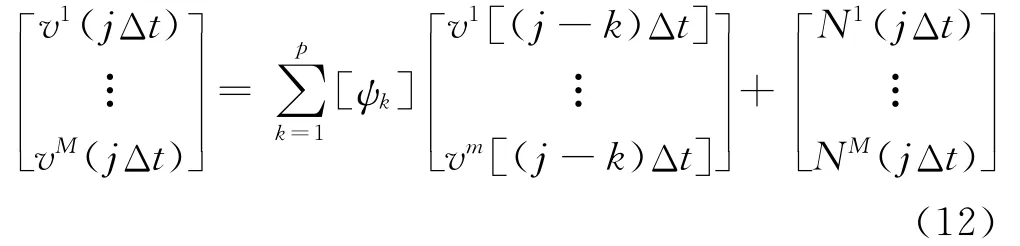
从而得出M个具有时间、空间相关，时间间隔的离散脉动风速过程向量.

1.5 脉动风载荷计算

当不考虑结构与风的耦合作用及漩涡影响时，根据Bernoulli定理，顺风向的风速分解为平均风速和脉动风速［7］，任一时刻t的风速v（z，t）为

则应对任一时刻t，任一高度z处的风压w（z，t）为

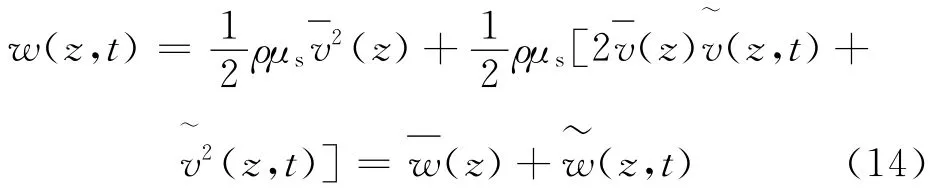
2 工程实例

图1所示为一建立在沿海附近的某型雷达发射天线装置，发射天线整体不配置纤绳，整体高度为10 m，其摇晃角度θ＜maxα＝15°（maxα为12级台风情况下发射天线允许的最大摇晃角度）；17级台风情况下，发射天线不损坏，不倒塌；使用寿命至少5年.杆身使用材料为Q275钢，许用应力σ＝275MPa，杨氏弹性模量为2.10×105MPa，泊松比为0.274，密度为7.85×10－6kg／mm3；结构中的法兰及加强筋，使用材料为2Cr13不锈钢，许用应力σ＝130MPa，杨氏弹性模量为2.28×105MPa，泊松比为0.3，密度为7.75×10－6kg／mm3.

图1 发射天线装置

2.1 天线结构脉动风载模拟及计算

本文采用AR法通过Matlab编程模拟了发射天线装置18个空间节点的时程风速（本文以2.95m、8.9m两点为例），模拟的参数如下：所处地面粗糙度类别为A类，地面粗糙度有关的指数α＝0.12，回归阶数p＝4，采样时间间隔为Δt＝0.1s，因本文模拟的是发射天线装置在强风17级下的脉动风载，故取模拟时间为60s.图2～3分别为17级强风在2.95m、8.9m两处的脉动风速时程曲线，从图4～5中的曲线描述可以看出，模拟功率谱与目标Davenport功率谱基本吻合，验证了AR模型描述风速谱的合理性.

图2 2.95m处脉动风速时程曲线

图3 8.9m处脉动风速时程曲线

图4 2.95m处风功率谱密度曲线

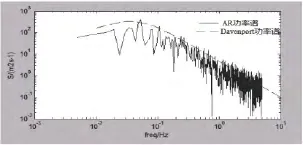
图5 8.9m处风功率谱密度曲线

由图2～5可看出：1）不同高度处脉动风速变化趋势相同，但各时刻的速度不同，表明脉动风速具有随机性；2）随高度增大，平均风速变大，但脉动风的波动区间变小，表明发射天线结构脉动风振作用随高度的增加而减弱；3）在高度不变时，各点的平均风速相同，但脉动风速不同，表明脉动风具有空间相关性.

根据风载荷计算公式，将脉动风速转换成脉动风压，得到2.95m、8.9m两处的脉动风压时程曲线，如图6～7所示.将Matlab计算出的数值加载到发射天线有限元模型上，如图8所示.

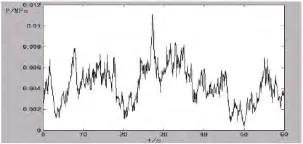
图6 2.95m处脉动风压时程曲线

图7 8.9m处脉动风压时程曲线

图8 发射天线模型施加载荷

图9 脉动风压下发射天线顶端最大偏移

图10 脉动风压天线顶端最大偏移时程曲线

图11 脉动风压下天线的等效应力

图12 脉动风压下天线的等效应力时程曲线

表1 17级脉动风压下的天线结构分析数值

将图10、12数值总结到表1可以看出，在0～60 s内，17级风脉动风压下天线的综合变形量最大值为578.2mm，最小值为438.7mm；等效应力最大值为268.5MPa，最小值为200.3MPa，针对本文对象使用材料的许用应力，根据分析计算结果需要对原结构加以优化改进.

2.2 天线结构地基受力及抗倾覆分析

本文中的某型雷达发射天线用于流沙地质环境下，岛屿上的强风很可能会引起雷达发射天线地基周围沙土的流动，使得地基部分裸露在地表，甚至会完全裸露，因此，考虑地基在强风作用下的受力及抗倾覆性是很有必要的.

对于发射天线的混凝土地基，体积约为8m3，本文分析天线地基在流沙环境下完全裸露在地表的情况，整体模型如图13所示.在发射天线杆上加17级风载荷，进行有限元计算分析.

图13 发射天线与地基整体模型

由图14～15可知，混凝土地基最大应力及最大综合变形量都出现在地基的中间位置，最大应力值为4.2MPa，最大综合变形量为1.15e－2mm，对比普通硅酸盐混凝土的强度指标，混凝土不会破坏.

图14 混凝土地基等效应力图（剖视）

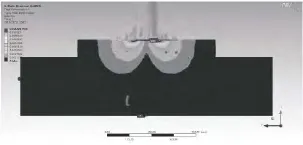
图15 混凝土地基综合变形图（剖视）

对于发射天线的混凝土地基，本文对混凝土地基的抗倾覆进行分析，故分析时将其底面一边固定约束，并在相对边所在面加等效力（当混凝土地基完全裸露在地表面时，其高度为2 000mm，根据风载荷特点，混凝土地基最高点处受风压最大，本文按最高点处的风压值计算出混凝土地基迎风面所受最大力），同时在发射天线杆上加17级风载荷进行分析.

根据分析结果可以看出，在混凝土地基完全裸露在地表面的情况下，混凝土地基将以地基的一边为支撑边有向上运动的趋势，混凝土地基沿Y轴向上的偏移量如图16所示.在17级风载荷下，此时混凝土地基在Y轴方向上最大偏移量为170.2mm，倾覆角度为4.9°，因此混凝土地基在17级强风作用下不会发生倾翻.

图16 发射天线整体偏移量

3 结 论

本文根据Davenport风速功率谱，用AR模型通过Matlab编程模拟出发射天线结构节点脉动风载时程曲线，脉动风在不同高度处的变化趋势基本相同，随高度增加，脉动风的波动区间逐步缩小，表明在发射天线结构中，高处的脉动性弱于低处的脉动性.将该谱运用于发射天线装置上仿真计算出在脉动风速下其受力响应情况，通过此方法可以在设计阶段检验结构的合理性、有效性.同时对实际工程中桅杆类高耸结构进行风载荷动力响应分析，特别是风振响应、疲劳分析时，需要先对不同等级参考风速工况进行脉动风速时程模拟，通过仿真模拟的方法来研究脉动风载荷对高耸结构及其地基的影响，可以为实际工程提供有效的方法.

［1］ 冯 甦，金 江.高耸钢塔结构的脉动风荷载模拟及结构风振响应分析［J］.南通大学学报：自然科学版，2007，6（1）：67－71.

［2］ 温德超，刘季林，王清刚.80m高钢烟囱的风振分析［J］.工程抗震，2004（1）：26－29.

［3］ 万春风，黄 磊，汪 江，等.脉动风作用下塔架结构的风振响应分析［J］.科技导报，2012，30（1）：39－43.

［4］ 彭 刚.时域分析法风载时程模拟［D］.广东：广东工业大学，2010.

［5］ 中华人民共和国建设部.GBJ135－90.高耸结构设计规范［S］.北京：中国建筑工业出版社，1990.

［6］ 埃米尔·希缪，罗伯特·H·斯坎伦.风对结构的作用－风工程导论［M］.刘尚培，译.同济大学出版社，1992.

［7］ 鲁丽君，瞿伟廉，李 明.桅杆结构脉动风速模拟与风载荷计算［J］.武汉理工大学学报：交通科学与工程版，2010，34（5）：1057－1060.