连续运动与超链接机制*——基于重庆地面及地铁交通流量数据的大尺度范围空间句法实证分析

盛 强 杨 滔 侯静轩 SHENG Qiang, YANG Tao, HOU Jingxuan

连续运动与超链接机制*——基于重庆地面及地铁交通流量数据的大尺度范围空间句法实证分析

盛 强 杨 滔 侯静轩 SHENG Qiang, YANG Tao, HOU Jingxuan

摘 要本文基于重庆市2010-2013年地面机动车流量数据及2014年地铁各站客流量数据，应用空间句法分析软件，分析了重庆城市大区域尺度范围内地面及地铁流量与空间线段地图分析结果的关联，验证了空间句法工具对城市大尺度范围流量分析的适用性。另外，基于地铁流量的实证数据，本研究重点对比测试了用空间句法分析地铁的两种建模方式：将地铁线路独立处理的“分离式”模型和将地铁线路纳入线段地图分析的“一体化”模型，发现“一体化”模型在分析站间截面流量时效果明显更好，但在分析进出站客流量时仅比“分离式”模型略好。作为结论，本文对地面和地铁两个问题的研究分别引出了连续运动和超链接两种空间机制，二者的共同作用使空间句法得以在超出视线和步行范围的大区域尺度上对城市进行有效分析。

盛强, 杨滔, 侯静轩. 连续运动与超链接机制——基于重庆地面及地铁交通流量数据的大尺度范围空间句法实证分析[J]. 西部人居环境学刊, 2015, 30(05): 16-21.

1 研究背景和意义

近年来，空间句法模型在国内外已广泛应用于对地面交通量和城市功能空间分布的研究和工程实践中，其以路网形态作为主要输入信息的简单建模方式赋予了模型很强的泛用性，但也不免引发来自各个方面的质疑，特别是在超出可视及可达原则适用范围的大尺度分析上。另外，空间句法对街道空间的抽象化处理能否适用于复杂的地形环境也是一个需要实证验证的问题。

针对以上两点，本文选取我国人口最多、面积最大的山地城市重庆作为研究对象，应用空间句法分析了重庆地区各主要道路的峰值交通量与一系列空间参数之间的关系，从实证数据分析的角度验证了空间句法在大城市区域尺度范围内车流交通量分析中的效果。另一方面，随着近期国内外学术界对低碳出行和TOD城市发展的关注，地铁对城市发展和出行的影响日趋重要。本研究基于2014年重庆现有地铁各站进出站流量数据及各站间截面流量数据，应用空间句法测试了两种建模分析方式对实证数据的分析效果，为日后在该方向上进一步探索适合的建模方式提供了经验。

*国家自然科学基金资助项目（51208343，51478300，51208334，51208346）；高等学校学科创新引智计划资助项目（B13011）

盛 强： 北京交通大学建筑与艺术学院，副教授，shengqiang1234@hotmail.com

杨 滔： 住房和城乡建设部城乡规划管理中心，副研究员，注册城市规划师

侯静轩： 英国空间句法公司北京办公室，助理分析员

最后，本文在理论上为空间句法在大尺度范围内分析的有效性作出了解释，认为尽管可视和可达性是空间句法对空间抽象的基础出发点，但现代交通技术的发展在大尺度空间行为上的影响往往表现为对速度日益增长的需求，这种需求导致了街道空间不断向连续性发展，并用各类公共交通以“超链接”的方式连接城市的各个场所。本文认为正是这两种机制使得以街区尺度空间特征为基础的算法得以应用于城市大区域尺度的分析中。

2 空间句法实证研究发展回顾

空间句法作为一种从建筑室内空间和街道空间拓扑连接关系的建筑和城市学理论及模型，缘起自20世纪70—80年代[1]，它为研究城市用地功能、经济与空间形态的关系提供了有效的模型工具。国内对空间句法理论的引进从20世纪80年代到近期一直在持续，东南大学段进教授团队[2]、张愚、王建国教授都对空间句法的基础算法进行过介绍[3]，最近同济大学肖扬、宋小冬和卡迪夫大学的Alain Chiaradia也对空间句法新算法的发展进行了梳理并提出了改进的建议[4]。由于目前国内对空间句法相关的介绍类文章已经比较多，但较少有以大量实证数据为基础的，以检验和开发探索模型新算法为目的的研究，而事实上，空间句法理论和模型的核心价值在于对数据的分析，并基于实证进一步探索适合的算法组合，发现和建立行为与空间之间的联系。当然，对于一些已经被实证多次验证过的分析方法，也有必要从理论上对其有效性的机制进行解释，以加深对该问题和模型工具的理解。

经历了30年的发展，空间句法实证研究成果积累最多的便是交通流量与空间形态之间的关系研究，而这也是诸如土地使用功能和社会行为等其他几个研究方向的基础。这些成果大都验证了城市空间的拓扑形态对流量有非常明显的影响。鉴于国内在这个方向上的工作还比较少，在这里需要简单说明以下两点：第一，对人流量的分析尺度多为一个街区的尺度，且往往需要对步行网络（含商业建筑内部主要廊道空间）进行细化处理，如果有诸如地铁等明显的人流吸引点，还需要应用Step Depth等工具叠加上吸引点的影响，具体做法可参见笔者近期发表的相关论文[5]。第二，对车流的分析往往需要稍大一些的尺度范围，如几个街区，且不适用于步行街区或交通量过大导致管控力度较大的区域（如单行道过多的情况）。在满足以上条件且地图和数据处理方法得当的情况下，车流量与空间参数的相关可达0.6~0.8，而步行人流量与空间的决定系数则在0.5~0.7。因此，从现有的实证研究来看，空间句法在大于街区的尺度范围内，对机动车流量的分析效果甚至比步行流量更好。

对本研究特别具有启发意义的研究为英国卡迪夫大学教师Alain Chiaradia基于地铁刷卡数据进行的伦敦地区空间句法分析[6]，以及他和UCL大学博士Stephen Law的后续研究[7]。他们的分析分别验证了将地铁线路与地面空间分离建模分析和将地铁与地面道路整合在一个模型中进行分析的方法（Multi-model），其结论显示，综合性模型的效果要好于分离建模分析的方式。

由于国内尚无基于地铁流量数据的空间句法实证研究出现，本文旨在以重庆的例子填补这个空白，同时也希望从这个实证案例出发，检验分离建模与综合建模的效果。这个过程本身也说明空间句法模型是一个研究性的、开放的理论及工具，并不存在对特定问题的唯一解答，而重点在于从空间的角度不断探索和思考的过程。

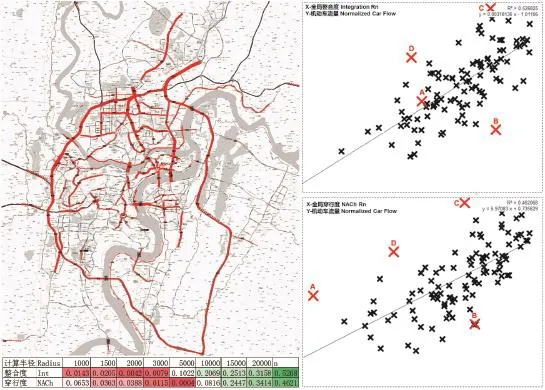
图1 重庆大区域尺度范围内124个道路截面的峰值机动车流量与空间全局整合度、穿行度回归分析Fig.1 regression analysis of the peak hour vehicle flow on 124 road sections in the metropolitan area of Chongqing with integration Rn and Nach Rn values respectively

3 对重庆大区域尺度地面交通流量的空间分析

本研究的数据来源为2010—2013年《重庆市主城区交通运行分析报告》，其具体流量数据涉及了重庆大区域尺度范围内85条主城区干道、18条内环快速路、21座跨江桥等共计124个道路截面的峰值流量数据（图1）。这些数据从量上来说并没有覆盖到一般城市道路和次级路的精度，但分布范围足够广，可以用作一个简单的案例。

本研究所建立的重庆大区域尺度空间模型涵盖重庆二环路内共计2420km2的广大区域，共34405条街道段，并包括了现有的地铁线路。在作地面流量分析时，为避免地铁线路的影响，没有将其纳入计算。本研究计算了1km、1.5km、2km、3km、5km、10km、15km、20km和全局半径的整合度（Integration）与穿行度（标准化角度选择度NACh）[8]。图1中列出了不同半径的整合度、穿行度与标准化处理后流量的决定系数。从分析结果来看，全局整合度与机动车峰值流量的相关程度最高，R平方值接近0.53，而与全局穿行度最高为0.46。

检查那些偏离回归线比较远的点发现：A点位于杨家坪环岛的一部分，导致实际流量远高于预测值，而这个因素是线段分析无法处理的；位于黄山大道中段上的B点流量值则远低于预测值，据百度地图显示，该道路很有可能受到两江幸福广场施工的影响。剔除A、B这两个点后，与全局穿行度R平方值提高为0.5071，与全局整合度R平方值可提高为0.5571。

这个结果虽然不如大多数已有的实证研究，但考虑到分析的尺度和数据自身的局限，还是比较令人满意的。一般来说，街区尺度的研究由于测点覆盖的街道段比例比较高，街道段之间的流量差异也比较大，分析结果往往比较好，特别是穿行度算法的优势会比较明显。而本研究的数据局限于城市的主要道路，忽略了大量次级道路，导致流量在宏观尺度范围内的差异影响比较大（中心区高、郊区低），使得全局整合度的结果比较有效（图2），全局穿行度则体现出层级明确的路网结构。因此可以想象，如果测点分布也深入到次级路和小路中，整合度的局限会越发明显，这个问题将在本文最后部分尝试解决。

无论是整合度还是穿行度，当代的空间句法线段分析算法都考虑到角度折转的因素，而这种算法的实际意义便是能够反映自然运动对连续性的需求。对车流交通来说，这个因素可能更加重要：随着速度的提升，接近于正前方向的空间体验距离被压缩得较侧向更加明显，而主要支持车流的超级街区在世界各个城市也往往呈现出连续网格的形态。这个原理被本文命名为“连续运动机制”，它可以从“车行”行为与空间的关系出发来解释空间句法为何能对超越视觉和步行可达区的城市街道系统进行有效分析。而下文将以地铁为例，说明另外一种使空间句法得以应用于大尺度城市分析的机制。

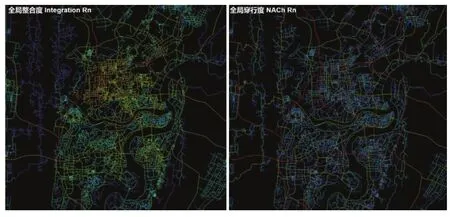
图2 重庆地区全局整合度（左）与全局穿行度（右）对比Fig.2 Comparison of the integration Rn (left) and Nach Rn (right) in Chongqing

图3 重庆市2014年地铁各站间截面日均总客流量（左）及各站进出站日均总客流量（右）Fig.3 daily passenger cross-section flow volume of each subway station (left) and daily passenger entering and exiting flow volume of each station (right) of Chongqing in 2014

4 对重庆地铁流量研究的两种建模方式的对比分析

应用空间句法分析地铁线路面临的技术问题是：空间句法目前较新的分析工具均以线段地图为基础，与传统纯粹分析拓扑空间结构的轴线地图相比，线段地图的优势在于考虑了真实距离和街道偏转角度（即方向）等因素。这类算法对于地面交通分析是合理且有效的，但在对地铁这种纯网络结构的研究中，线段地图的优势反而会成为局限性，因为地铁乘客完全是在一维空间中运动的，方向性的意义非常有限。轴线地图分析工具虽然是纯拓扑的、一维的，但这种优势又很难被自然地带入线段地图分析。简单来说，目前我们尚缺乏一种整合二者各自优势的平台，而这种整合既需要算法上的可行性，又需要实证上的合理与有效性。针对于此，本研究将基于空间句法已有的算法，在组合应用的方向上进行一些探索。

截至本研究开始时（2014年7月），重庆有5条投入运行的地铁线路：1号线、2号线、3号线、6号线和国博线。本研究的地铁客流量数据根据2014年2月工作日的平均客流量统计，图3中分别展示了各个站点间的截面客流量和日均进出站客流量统计。从图中看，各线路大体呈放射状，截面流量规律比较明显，最集中的区域为东西向的渝中半岛和南北向连接观音桥与南坪两站的十字区域，向两边则逐站递减。进出站客流量虽也有一定的相似趋势，但微观上体现出较大的差异性，相邻站点间流量差异很大。比较这两类数据可以发现，截面流量体现出过境交通的特点，进出站流量则体现出站点周边功能对人流的吸引作用。

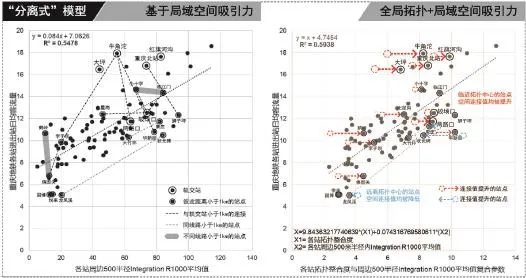
图4 基于局域空间吸引力（左）与叠加站点网络整体拓扑连接修正后的预测模型对比（右）Fig.4 comparison of prediction model based on local area attraction (left) and prediction model of connected and modified superimposed station network topology (right)

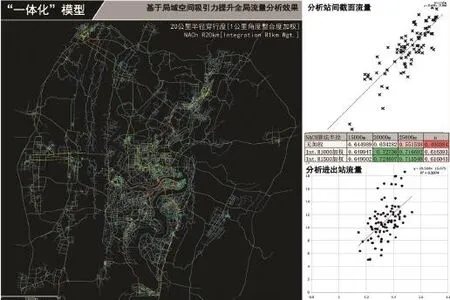
图5 “一体化”模型对站间截面流量和进出站客流量的分析Fig.5 integration model analysis of the inter-station cross-section passenger flow and entering/exiting station passenger flow

首先尝试用“分离式”建模的方式进行分析。这种方式的特点是理论上简单，回避了轴线分析与线段分析结合的难点。根据现有站点建立两个忽略地面街道网络的轴线简图：一种将站点之间的线路作为计算单元，抽象为一条直线，该模型用于计算两个站点间的截面流量；另一种将站点作为计算单元，该模型用于分析进出站客流量。需要说明的一个技术细节是，在不同线路之间切换（轨交站）时，本研究经过试验最终采用了3个拓扑步数作为换乘的阻尼，而这个结果也证实了Alain Chiaradia早期的研究。

从分析结果来看，尽管此模型完全忽略了复杂的地面路网而仅仅考虑了各站点之间的拓扑连接，对截面流量分析的决定系数R平方值还是轻松达到了0.4983，而对进出站客流量的决定系数仅为0.22，不足以用于预测。

由于进出站客流量是出行目的的体现，因此对其起决定作用的应该主要是分布于站点周边一定半径内的城市功能。而从空间句法的理论来说，站点周边的功能分布也受到这些街道在城市整体空间中的连接参数的影响：空间连接好的街区往往更有活力，有更多的商业分布，成为出行的目的地。也就是说，分析进出站客流量主要应分析地面街区的空间吸引力，而非地铁站点拓扑结构的吸引力。

基于这个假设并依循Alain Chiaradia的做法，本研究尝试统计了各站点500m半径内的平均整合度参数。由于位于线路尽端部分的几个站点（五里店、大学城、江北机场）往往有更大的辐射范围（特别是在远郊区），因此真实流量远高于预测流量。剔除这3个点后，1km、1.5km、2km和5km半径的整合度平均值与进出站客流量的R平方值分别为0.5478、0.5466、0.4924和0.2789。这个结果印证了局域空间吸引力对地铁进出站客流量的预测力：站点周边500m内街道密集且接近网格、彼此通达性好的空间肌理有更大的几率成为地铁出行的目的地。

更细致的分析如图4左侧的散点图，各个换乘站（大坪、牛角沱、红旗河沟）以及作为铁路—地铁“轨交站”的重庆北站明显有高出预测值的进出站人流。另外，在城市的中心和副中心区，彼此距离小于1km的站点在图中以虚线连接。不难发现如牛角沱等轨交站明显“抢夺”了周边临近站点的客流量，使得某个站点的客流量超过预测值，而其他临近站点的客流量降低。

尽管基于站点拓扑网络连接计算的流量预测仅有0.22的决定系数，但它却能从宏观上把握城市大体的中心区域。这个特点使得该算法有必要与纯基于局域空间吸引力的模型相结合。本研究基于二元一次回归分析建立了基于这两个因子的预测模型，如图5右侧的散点图所示，其决定系数可达0.5938。另外，从图中也可以明显看出叠加的效果，大部分临近拓扑网络中心的站点可以获得额外的连接性加成，而这些站点往往也位于城市中心渝中半岛；边缘的线路则由于远离拓扑中心而被进一步弱化。

作为对比，“一体化”模型将地铁线路也作为直线绘制在轴线地图中，使用unlink工具使之与地面道路分开。该模型在Stephen Law和Alain Chiaradia的文章中被证明更有效。简单起见，本研究首先验证“一体化”模型对地铁各站间截面流量的分析能力。

图5右中部为各半径穿行度算法与截面流量的相关程度，如不使用加权算法，则15km半径的穿行度与截面流量R平方值可达0.645，高于“分离式”模型中用简单站点间拓扑网络连接得到的结果0.4983。本研究使用的加权为基于小尺度范围（1km和1.5km）半径整合度计算结果的大尺度范围穿行度计算，这一算法更能体现出各个区域的吸引力引发的大尺度范围运动。从结果来看，1km半径整合度加权计算的20km穿行度可达0.727，提升作用非常明显。另外，通过计算各地铁线路与地面街道连接线的加权20km穿行度数值，其结果可理解为地铁的全局可达性，它与进出站流量进行回归分析的R平方值为0.3074，同样明显高于运用“分离式”模型得到的0.22的结果。

同样的，对进出站流量的深入分析主要基于对局域空间吸引力的计算。在“一体化”模型里，本研究对比了站点周边500m可达范围内计算半径在1km、1.5km、2km和5km整合度的平均值，其结果证明，1km半径整合度与进出站客流量最为相关，R平方值可达0.5841。这个结果与“分离式”模型发现的计算半径相同，但结果好于后者（0.5478）。其原因可以从图6左侧的散点图与“分离式”模型的局域空间吸引力散点图对比中发现：由于部分地铁站点之间的距离小于1km，这些短程连接的站点形成的片区在“一体化”模型中的整合度数值会被明显提高。而从这些站点的分布来看，它们往往位于城市的中心区。这在客观上达到了与“分离式”模型中叠加站点全局拓扑连接类似的效果，这也意味着在其他城市中应用此模型分析时，需要根据该城市实际站点分布的状况酌情确定分析半径，才能使它发挥最大的效果而成为一个非常有效的预测工具。

之前的截面流量分析中关于进出站客流的分析成果可以被理解为表达了地铁网络的全局可达性。本研究也尝试将这个相对独立的因子与表达局域空间吸引力的因子联立进行二元回归分析。从结果来看，其R平方值可达0.6116，仅比“分离式”模型0.5938的结果略好。图6右侧的散点分析试图解释全局可达性提升分析效果的机制：通过对比全局可达性高的站点在地图上的分布可以发现，它们多位于主要道路的交点，同时在市中心也分布较多。这造成大部分经二元回归分析后空间连接参数提升的站点多分布于散点图的右上角，而降低的多集中在左下角。但必须指出的是，这个结果同样暗示着地铁与地面道路网络的相互作用：大路节点周边往往可达性较好，特别是经过1km整合度加权算法强化出的区域，往往同时也有完善的小尺度街格。而在“一体化”模型中，地铁和地面线路是等同处理的，存在着流量相互影响的情况，因此很难明确量化地说明其具体机制。所以，尽管在此案例中其计算结果稍好，也有待进一步的深入研究。事实上，笔者倾向于支持将“一体化”模型的局域空间吸引力分析与“分离式”模型中基于站点拓扑网络计算出的全局可达性联立作二元回归分析，其结果为0.602，分析的效果不差，但在理论上要解释的问题却简单得多。

图6 基于局域空间吸引力（左）与叠加全局可达性修正后的预测模型对比（右）Fig.6 comparison of prediction model based on local area attraction (left) and prediction model of modified superimposed overall accessibility

无论采用哪种方法，从地铁的案例分析中我们可以体会到空间句法在大尺度空间分析中的另外一种机制：超链接机制。超链接源自网络中的超文本（Hypertext），意指从一个地点/文本瞬间到达另一个地点/文本而忽略掉中间的过程。当代城市中的公共交通体系或环路、高速路等道路体系都可以被理解为一种城市超链接的工具，便于我们从一个场所“直接”到达另一个场所。但值得注意的是，拉动我们建立和使用这些超链接工具的原动力还是城市中各种吸引人的场所，那些有特色的、充满活力的街区和建筑的集合[9]。从地铁的案例中不难发现，解释进出站客流量最有效的工具是各站点周边的空间形态参数，而全局性的空间参数对模型的贡献很小，这个现象清晰地表达了超链接机制的作用。

5 “机制背后的机制”——空间句法对背景性运动和前景性运动的处理方式

问题到这里还没有结束。真实的城市中，连续运动和超链接机制往往是共存的。撇开公共交通系统不谈，即便是私家车出行也同时受到决策时的超链接机制和过程中的连续运动机制控制。目的性交通（To-Movement）和穿行性交通（Through-Movement）是空间句法理解城市空间与功能之间关系的基础。空间句法毕竟不是专业进行交通分析的软件工具，它的作用主要在于分析空间形态对运动的影响，或者说一种城市中“背景性”的运动；与之相对的是一些由特定吸引点引发的“前景性”运动，比如医院、购物中心或地铁、火车站等。但这并不是说空间句法对此无能为力，通过叠加吸引点，或者本研究中的权重算法，都可以实现对“前景性”运动的拟合和提升分析效果。问题的关键在于这个权重如何去加：由于交通模型的目的是发现可能出现拥堵的极限点，故多采用根据特定功能面积总结出来的数据；而空间句法的目的多在于描述城市空间对各类功能的支持，或者说其潜力，直接按功能确定权重的实际应用意义就不大了。因此，本文采用的权重算法来源于空间自身的吸引力，这种叠加方式是对其基本理念的坚持而非妥协。另一方面，单纯追求高R平方值也是没有意义的：如在地铁的案例里，对各站间截面流量的分析获得了很好的结果，但地铁流量属于“非参与性交通”，对城市空间没有直接的贡献，并不能激发沿途的功能；车流则是参与性的交通，能够对沿途的城市功能产生更直接的影响。因此，尽管“一体化”模型在分析地铁站间截面流量上完胜“分离式”模型，其实际意义也是非常有限的，而其理论意义倒是证明了超链接机制的作用。同时，在实践中可以进一步思考该方法应用于车行交通的可能性：回到文章开始部分在分析车流时遗留的关于整合度和穿行度的问题，我们可基于地铁分析方法的启发，将车流理解为局域尺度范围内目的性空间吸引下特定尺度范围的运动。图7展示了以7.5km半径整合度分析为加权的全局穿行度计算结果，与重庆大区域尺度车流量交通的相关R平方值为0.612，高于全局整合度和全局穿行度的结果。这个例子可以说明，连续运动机制也可以被理解为超链接机制的一种特定形式。引入角度的拓扑算法在大尺度上近似地将一段弯曲的道路作为“一组数值接近的”计算单元，就如同忽略了具体形态而直接连接的地铁线路一样。

图7 对重庆大区域车行交通的复合式空间分析Fig.7 compound spatial analysis of traffic in the large region of Chongqing

最后，有必要阐述一下本研究的局限性。首先，对局部空间吸引参数的引入最好有地铁周边实际城市功能分布的实证数据支持，对这一点笔者将另撰文详述。另外，如本文开始部分提到过的，选择重庆的一个目的在于尝试挑战山地城市的复杂环境，但山地环境使得建造道路的成本变得更高而更难形成网格肌理，在碎片化的路网之间运动便被局限在少数对外连接其他区块的道路、桥梁或隧道上。这无形中反而降低了分析难度，并且也放大了地铁连接的效果，针对地铁的研究无疑还需要更多其他类型的实证数据支持。但从另外一个角度来说，重庆复杂多变的城市街道更像是一个微缩版的城镇群大区域模型。放大分析尺度，真实的平原地区城镇分布和连接状态可能也不过如此。因为在大区域尺度上空间连接的成本同样变得很高，因此其层级性也必然会表达得更加明显，这使空间句法分析的效果反而变得更好。

参考文献：

[1] Hillier B, Hanson J. Social Logic of Space[M]. London: Cambridge University Press, 1984.

[2] 段进, 希列尔. 空间研究3：空间句法与城市规划[M]. 南京: 东南大学出版社, 2007.

[3] 张愚, 王建国. 再论“空间句法”[J]. 建筑师, 2004, 109(03): 33-44.

[4] 肖扬, Chiaradia A, 宋小冬. 空间句法在城市规划中应用的局限性及改善和扩展途径[J]. 城市规划学刊, 2014, 218(05): 32-38.

[5] 盛强, 杨滔, 刘宁. 目的性与选择性消费的空间诉求——对王府井地区及三个案例建筑的空间句法分析[J]. 建筑学报, 2014(06): 98-103.

[6] Chiaradia A, Moreau E, Raford R. Configurational Exploration of Public Transport Movement Networks: a Case Study, the London Underground[C]// 5th International Space Syntax Symposium, 2005.

[7] Law S, Chiaradia A, Schwander C. Toward A Multi-model Space Synatx Analysis: A Case Study of the London Street and Underground Network[C]// 8th International Space Syntax Symposium. Santiago de Chile: PUC, 2012.

[8] Hillier B, Yang T, Turner A. Advancing DepthMap to Advance Our Understanding of Cities: Comparing Streets and Cities, and Streets to Cities[C]// 8th International Space Syntax Symposium. Santiago de Chile: PUC, 2012.

[9] 赵启东, 魏皓严. 步行化的概念与实践——城市中心步行化发展历程的时空双维度分析[J]. 西部人居环境学刊, 2014, 29(02): 20-29.

图片来源：

图1-7：作者根据相关数据绘制

（编辑：郑曦）

中图分类号TU984.14

文献标识码B

文 章 编 号2095-6304(2015)05-0016-06

DOI:10.13791/j.cnki.hsfwest.20150503

作者简介

收稿日期：2015-09-01

Continuous Movement and Hyper-link Spatial Mechanisms —A Large-scale Space Syntax Analysis on Chongqing’s Vehicle and Metro Flow Data

关键词空间句法；大尺度范围分析；地铁客流量；地面机动车流量；山地城市Abstract: This paper presents a space syntax analysis on the flow of vehicle from 2010-2013 and metro flow data on 2014 in Chongqing. The research verifies the effect of space syntax analysis at large scale. Furthermore, this paper emphasizes the analysis of metro flow data by comparing to the way of modelling in space syntax: a separated model and an integrated model. The result shows the integrated model clearly works better when analyzing the flow intensity between stations, but only slightly better when analyzing the flow of people coming in and out of the station. As a conclusion, this paper claims two spatial mechanisms that establish the validity of the space syntax model at large scale: the continuous movement and hyper-link spatial mechanisms.

Keywords:Space Syntax; Large-scale Analysis; Metro Flow; Vehicle Flow; Hilly Landscape