旋转的奥秘

蒋明玉

同学们，我们生活在运动的世界里，风吹树梢动，鸟儿飞翔翅膀动。其实我们的数学世界也因为有了动而变得丰富多彩。现在让我们做实验来感受一下吧！

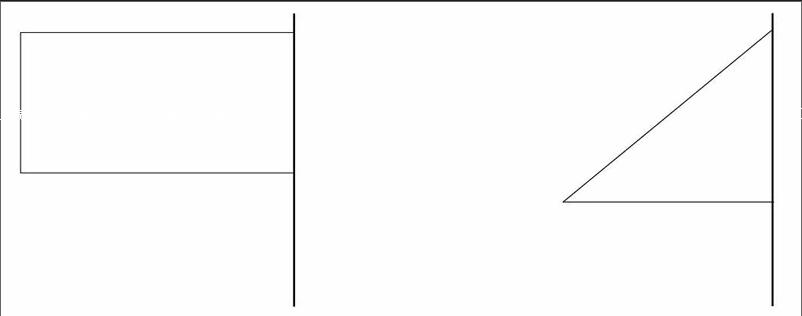
在课前蒋老师就让同学们做了长方形、直角三角形的小旗（如下图）。“现在请大家将旗杆快速旋转一周，看看，你发现了什么？”蒋老师问。

小明立刻说：“左边长方形的小旗旋转一周能够形成一个圆柱，圆柱的底面半径是长方形的长，圆柱的高就是长方形的宽。”

张宁接着说：“右边直角三角形的小旗旋转一周能够形成一个圆锥，圆锥的底面半径是直角三角形的一条直角边，圆锥的高是直角三角形的另一条直角边。”

蒋老师微笑着说：“对，一个长方形经过旋转可以形成圆柱体，一个直角三角形经过旋转可以形成圆锥体。那么如果左边长方形的小旗的长是5厘米，宽是2厘米，你能求出旋转出的那个圆柱的体积是多少吗？”

蒋帅同学很快在黑板上写出：3.14×5²×2=157（立方厘米）。

“看来同学们对圆柱体和圆锥体已经很熟悉了，那接下来蒋老师可要考考大家了！”说完蒋老师在黑板上写下题目。

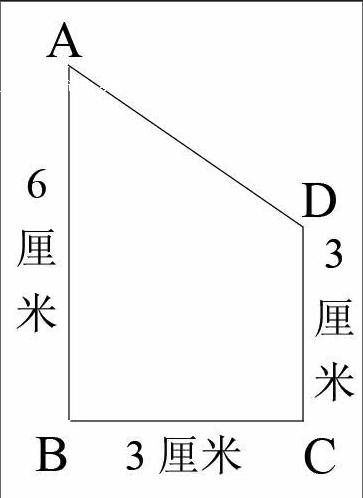
如右图，ABCD是直角梯形。以AB为轴将梯形旋转一周，得到一个旋转体；以CD为轴将梯形旋转一周，也得到一个旋转体。哪个旋转体体积大一些？

小明不假思索就说：“我觉得以AB为轴旋转的旋转体大一些。”

蒋帅则认真地思考并计算起来：

以AB为轴旋转的旋转体是由一个圆柱和一个圆锥组成的立体图形，圆柱的体积是3.14×3²×3=84.78（立方厘米），圆锥的体积是1/2×3.14×3²×3=28.26（立方厘米），84.78+28.26=113.04（立方厘米）。以CD为轴旋转的旋转体是一个圆柱和缺少一个圆锥的圆柱组成的，圆柱的体积是3.14×3²×3=84.78（立方厘米），缺少一个圆锥的圆柱的体积就是圆柱体积的2/3，算式为2/3×3.14×3²×3=56.52（立方厘米），84.78+56.52=141.3（立方厘米）。通过计算可知，以CD为轴旋转的旋转体体积大一些。

“同学们，做数学题仅仅凭感觉是不行的，要凭事实说话。”蒋老师说。

这时，爱思考的张宁急忙站起来，说：“若换一个角度想想，根本不用上面那样烦琐的计算，就很容易发现以CD为轴旋转的旋转体体积大一些。以AB为轴旋转的旋转体是由一个圆柱和一个圆锥组成的立体图形，圆柱和圆锥等底等高，如果圆锥的体积看作1份，那么圆柱的体积就是3份，一共就有4份。而以CD为轴旋转的旋转体的体积，上面的旋转体的圆柱挖去了一个圆锥（1份），所以上面余下部分的体积有2份，加上底下圆柱的体积3份，一共就有5份。所以，很容易知道以CD为轴旋转的旋转体体积大一些。”

蒋老师赞许地向张宁点点头，说：“同学们看，简单的动就将这些平面图形变成了我们熟悉的立体图形，今后我们要多观察、多操作，深入探索数学世界的奥秘！”