“地球与地图”专题

徐桂　吴忠芳

一、考纲解读（表1）

二、考点层析

考点1：经纬网及其地理意义

【图释考点】（图1）

【疑难突破】

1.定“位置”

地球上除了极点外，任何地点都有一定的经度和纬度，这是区域定位的重要方法。

2.定“方向”

理论依据：经线指示南北方向，纬线指示东西方向。

（1）方格状经纬网图。①确定南北方向：在南北半球的两点，北半球在北，南半球在南；同在北半球，纬度值大者在北；同在南半球，纬度值大者在南。②确定东西方向：同在东经度，经度值大者在东；同在西经度，经度值大者在西。若分别在东西经，二者之和小于180°，东经度地点在东，西经度地点在西；二者之和大于180°，东经度地点在西，西经度地点在东。

（2）弧线式经纬网图。①两点位于同一纬线上，根据自转方向判断东西；②两点位于同一经线上，根据极点位置判断南北；③两点既不在同一经线上，也不在同一纬线上，根据经度、纬度分别判断东西、南北。

3.定“距离”

两点位于同一经线上根据纬度差定经线长度，纬度相差1°，实际距离长约111千米；两点位于同一纬线上，根据经度差定纬线长度，纬线长度由低纬向高纬递减，经度差1°，其长度大约是111×cosα千米（α为该纬线的纬度数值）。

4.定“范围”

相同纬度且跨经度数相同的两幅图，其所示地区的面积相等；跨经纬度数相同的地图，纬度越高，表示的实际范围越小。

5.定“最短航线”

地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。（注：所谓大圆指过地心的平面与球面的交线，如赤道、经线圈、晨昏圈等）

6.定“对称点”

关于赤道对称的两点：经度相同；纬度相反，数值相等。关于地轴对称的两点：经度相反，度数互补；纬度相同。关于地心对称的两点：经度相反，度数互补；纬度相反，数值相等。

考点2：等高线地形图

【疑难突破】

1. 等高线地形图中的相关计算

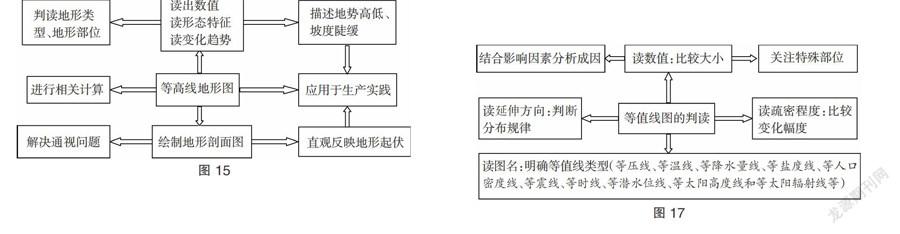
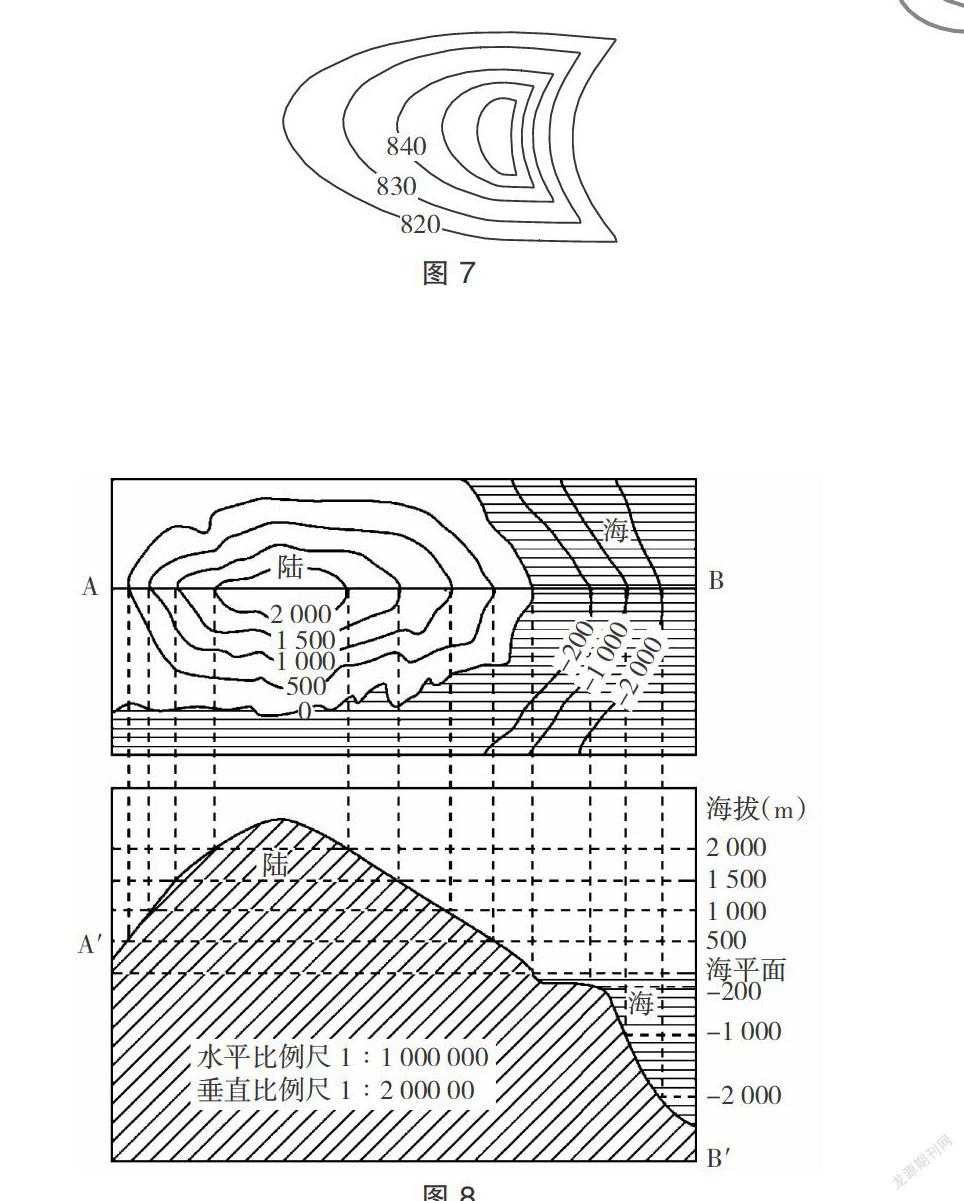
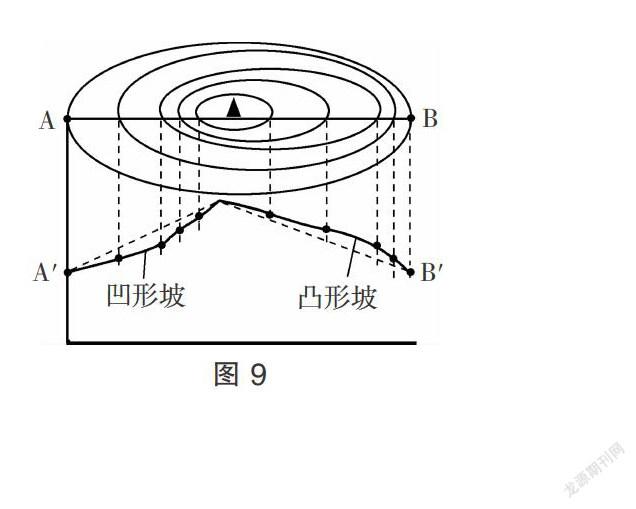
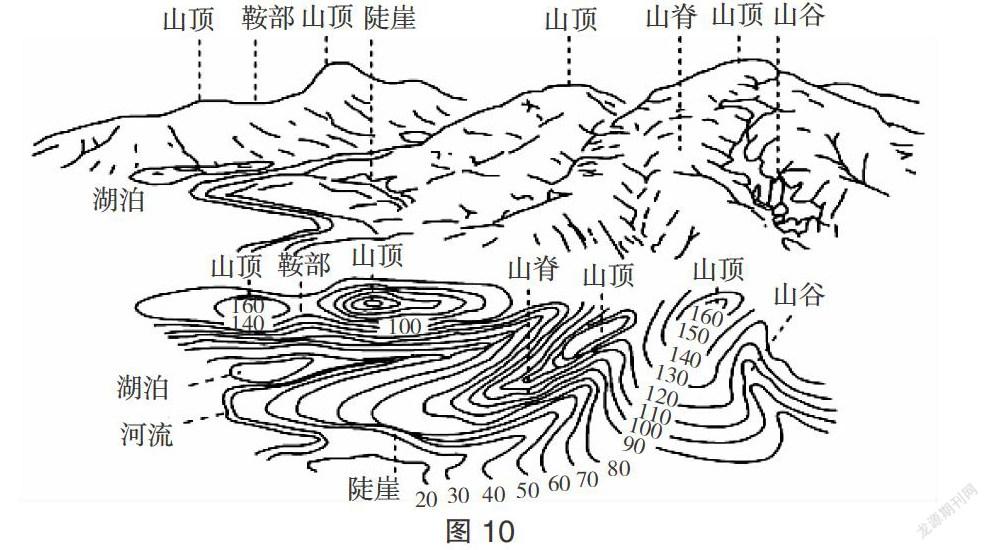
（1）计算两点的相对高度和温差。读出任意两点的海拔高度或范围，计算出两点的相对高度或最大可能值和最小可能值，根据气温垂直递减率（0.6℃/100米）可计算两地间的气温差：T差=0.6×H相/100。

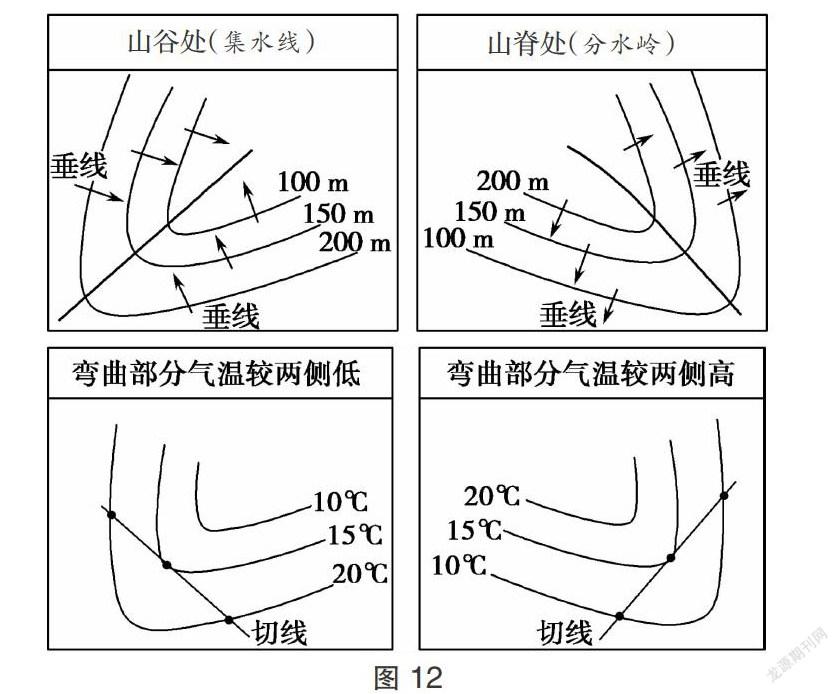
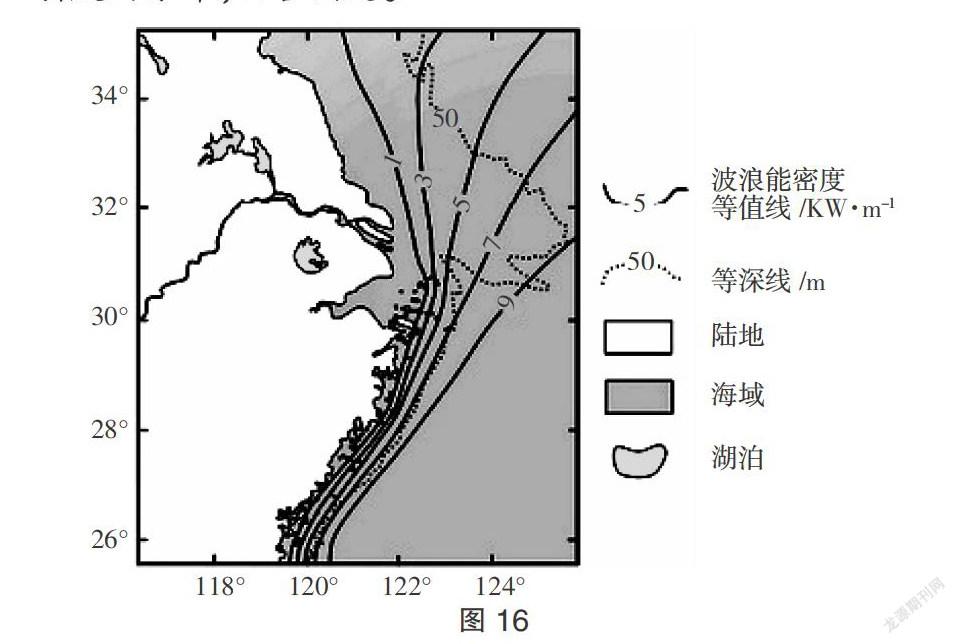
（2）估算陡崖高度。①陡崖的相对高度ΔH取值范围是：（n-1）d≤ΔH<（n+1）d。②陡崖崖顶的绝对高度：H大≤H顶

（3）闭合等高线区域内海拔高度的判断。位于两条等高线之间的闭合区域，如果其值与两侧等高线中的较低值相等，则闭合区域内的海拔高度低于其等高线的值；如果闭合等高线的值与两侧等高线中的较高值相等，则闭合区域内的海拔高度比其等高线值更高，即“大于大的，小于小的”。如图2所示，图中等高距为100m，A地的海拔高度在400m和500m之间，B地的海拔高度在200m和300m之间。

2.部分特殊地貌的等高线地形图

（1）冲积扇：河流（山间洪流）在出山口处因流速减小，其携带物质铺散沉积而形成的扇形堆积体。冲积扇的地面由扇顶到扇缘坡度由陡变缓，等高线多呈圆弧形，且上密下疏（如图3）。

（2）梯田：在坡地上分段沿等高线建造的阶梯式农田。梯田等高线图表现为梯田田埂处等高线较密，田面等高线稀疏（如图4）。

（3）岱崮（方山）地貌：“崮”的顶部平展开阔，外表呈圆形或方形，峰巅周围峭壁如削，峭壁下面坡度由陡到缓。等高线地形图中崮顶等高线稀疏，外围为陡崖（等高线上标有示坡线），向山麓过渡等高线由密集变稀疏（如图5）。

（4）蘑菇石：由于基岩岩性的差异常被侵蚀成顶部大、基部小，形似蘑菇的岩石。等高线地形图中蘑菇石基座因被高处蘑菇石遮挡，用虚线表示，而高处则用实线表示（如图6）。

（5）新月形沙丘：在风力作用下由沙粒聚成的沙堆。等高线地形图中沙丘迎风坡凸而平缓 ，背风坡凹而较陡（如图7）。

考点3：地形剖面图的绘制与判读

【疑难突破】

1.地形剖面图的绘制方法（以图8为例）

（1）找控制点。剖面线与等高线所有的交点、剖面线与河流所有的交点和剖面线经过山顶或山谷底部的点均为控制点。

（2）定比例尺。根据数据，确定水平比例尺和垂直比例尺。

（3）画矩形（或直角坐标系）。根据已确定的比例尺画出合适的矩形（或直角坐标系）。

（4）标注水平点。根据水平比例尺将所有控制点标注在横坐标上。

（5）作虚线。按高程作横坐标的平行虚线；按水平点作纵坐标的平行虚线。

（6）连线。将各控制点按其海拔在相应的垂直虚线上标出相应的点，并用平滑曲线将各点连接，即为符合要求的地形剖面图。

2.通视问题

通视问题可通过作地形剖面图（如图9）来解决。如果过已知两点作的地形剖面图无障碍物（如山地或山脊）阻挡，则两地可互相通视。特别注意“凹形坡”与“凸形坡”的不同。从山顶向四周，等高线先密后疏，为“凹形坡”，可通视；等高线先疏后密，为“凸形坡”，“凸形坡”容易挡住人们的视线。

考点4：其它等值线图

【疑难突破】

1.等值线的共性特征

（1）同线等值：同一线上的点数值相等。

（2）等值距相同：在局部图中任意相邻的两条等值线的差值为0或一个等值距（可大于或小于一个等值距）。

（3）等值线是闭合曲线（在一幅图中因受图幅限制，局部等值线不一定闭合）。

（4）等值线不相交（陡崖除外）。

（5）弯曲处：低值凸向高值，凸处的值变低；高值凸向低值，凸处的值变高。

（6）疏密：等值线越稀疏，单位距离的差值越小；等值线越密集，单位距离的差值越大。

（7）局部小范围闭合区：位于两等值线之间的闭合区域，表示数值不在两线数值的正常范围之内，判读方法遵循“大于大的”或“小于小的”规律。

2.常见等值线图的应用

通过等高线判断地形的种类（山地、盆地、高原、山脊线、山谷线、陡崖等）、坡度陡缓，确定山脉走向、选择水库大坝的位置、确定公路线的走向、绘制地形剖面图及估计工程土方等。

通过等压线判断气压系统名称，如低气压、高气压、高压脊、低压糟；判断不同气压系统的天气特点、风向与风力大小等。

通过等温线判断所在地位于的南北半球、季节与天气以及该季节大陆与海洋上的气压中心、季风盛行方向（亚洲东部和南部）。

通过等降水量线结合具体的地形轮廓判定山地的迎风坡与背风坡、距海远近、山脉走向等。

三、图像突破

1. 等高线地形图的判读

【图型解读】

等高线地形图中主要地形部位如图10所示。

【判读方法】

（1）根据海拔判读地形类型：海拔200米以下，等高线稀疏为平原；海拔500米以下，相对高度小于200米为丘陵；海拔500米以上，相对高度大于200米，等高线密集为山地；海拔高，相对高度小，等高线边缘处密集，顶部稀疏为高原；四周海拔高，中间海拔低为盆地。

（2）根据等高线形状判读地形部位：山顶为闭合等高线，数值从中心向四周逐渐降低；盆地或洼地为闭合等高线，数值从中心向四周逐渐升高；鞍部为两个山顶中间的低地，形似马鞍；等高线向海拔低处凸出为山脊；等高线向海拔高处凸出为山谷。

（3）疏密程度：密集处坡度陡；稀疏处坡度缓。

2.等值线图的判读

【图型解读】

图11为某地区年降水量分布图（单位：mm）。等值线上最大值为1 500，最小值为900；A与B相比，A处等值线密集，B处稀疏；C处等值线由南向北弯曲。

【判读方法】

（1）读图名：明确等值线图所要反映的地理事物。

（2）读数值范围和极值：最大值、最小值，不在线上的点为范围值。

（3）读疏密程度：等值线密集，表示其数值变化幅度大；等值线稀疏，表示其数值变化幅度小。

（4）读弯曲方向：确定弯曲部分为高值区还是低值区，一般采用垂线法和切线法（如图12）。①垂线法：在等值线图上弯曲最大处的两侧作各等值线的垂线，方向从高值指向低值。若箭头向中心辐合，则等值线弯曲处与两侧相比为低值区；若箭头向外围辐散，则等值线弯曲处与两侧相比为高值区。②切线法：在等值线弯曲最大处作某条等值线的切线，比较切点与切线上其它点的数值大小。若切点数值小于其它点的数值，则该处为低值区；若切点数值大于其它点的数值，则该处为高值区。

（5）读局部小范围闭合等值线：闭合线内数值应用“大于大的，小于小的”规律来确定。

（6）读延伸方向：等值线数值递增或递减方向反映该地理事物的变化规律。

（7）读特殊部位：关注等值线图中特殊部位，如等高线相交处的陡崖；等值线特别密集处，如等压线非常密集且气压较低的环形区域可能存在台风等。

四、思维建模

1.地形特征的分析思路

【典例精析】

（2015年四川卷）阅读材料，回答问题。

材料： “蓉欧快铁”运行线路图（图13）；甲区域等高线地形图（图14）。

据图14，描述图13中甲区域的地形特征。

解析：由等高线高程数值为1 500米到4 000米，相对高度大于2 500米，结合所处位置，再根据等高线分布的疏密，可判读该地地形及地势起伏。

答案：高原、山地为主；高原分布在西南（南）部和东北（北）部，山地主要分布在中部；地势起伏大，西南（南）高，东北（北）低。

【以例得法】

（1）分析角度。①获取信息：在等高线地形图中读出海拔和等高线分布的疏密。②描述表达：地形类型，地势高低、起伏大小。③知识应用：根据等高线图还可进行相关计算，选择水库大坝的位置、修筑公路线的走向选择，工农业生产区位选择等。

（2）以例建模（图15）。

2.等值线图的分析思路

【典例精析】

（2015年福建卷）图16示意我国沿海局部海域波浪能密度的分布，回答问题。

指出该海域波浪能密度大小的南北差异，并分析其原因。

解析：从图示波浪能密度等值线数值分析，北部密度较小，南部密度较大。其原因是受海域水深影响，从等深线数值及分布分析可知，北部海域数值小，分布稀疏，表明大陆架宽浅，海底摩擦作用大，波浪能密度较小；而南部海域水深，海底摩擦作用小，波浪能密度较大。

答案：差异：北部密度较小，南部密度较大。原因：北部海域大陆架宽浅，海底摩擦作用大，波浪能密度较小；南部海域水深，海底摩擦作用小，波浪能密度较大。

【以例得法】

（1）分析角度。①分布特点：哪儿多（大），哪儿少（小）；总体趋势，特殊部位。②成因：明确其影响因素、主导因素、能论证结果的因素。③数值变化：从哪儿向哪儿递增（递减），变化幅度大（小）。

（2）以例建模（图17）。