一种滤除表面肌电信号中工频干扰的新型方法
汤 烈,葛良全
(成都理工大学 信息科学与技术学院,四川 成都 610059)
0 引言
表面肌电信号(Surface⁃Electromyography)包含一定区域内肌肉活动的原始信息以及多种不可避免产生的噪声[1]。
这些噪声严重影响了SEMG信号检测,而工频干扰作为生物信号采集中一重要干扰源[2]正好落入SEMG信号的主要信号频率范围内,随时间相位和频率发生变化的工频噪声更加难以滤除,使得滤除在SEMG信号检测中的工频干扰技术尤为关键。近年来,已经有多种滤除工频干扰的方法应用在SEMG信号检测中。包括:利用带阻滤波器在电路上滤除工频干扰[3],也有利用数字陷波器,将采集的模拟信号量化为数字信号后,利用频谱插值法[4]、自适应滤波[5]、小波变换[6]等进行滤波处理。
本文首先在硬件电路上使用抑制工频干扰的方法,并在其后提出一种基于经验模式分解(Empirical Mode Decomposition)[7],使用自适应滤波器的滤除EMG信号采集中的工频干扰。使用自适应滤波器来滤除工频干扰,首次是由 B.Widrow提出的[8]。通过EMD分解得到的若干个本征模态函数(Intrinsic Mode Function)分量具有不同的频率成份和不同带宽,同时其频率成份和带宽是由分解信号的不同而变化的,即EMD分解方法也可看作是一组具有自适应特性的带通滤波器[9],由于IMF的频率分辨率具有自适应性,同时其还具有自适应的滤波特性;将SEMG信号通过EMD分解为一系列本征模态函数IMF,而工频干扰可大致模拟为正弦信号,且可被视作为一个IMF函数进行选择性重建,使用该函数作为自适应滤波器的参考输入,即可完成自适应完成滤波。在EMD算法的基础上,为提高算法性能,经过数据对比,采用EMD算法的优化算法集合经验模式算法(Ensemble Empirical Mode Decomposition)算法替代EMD算法,并选择最小均方算法(LMS)算法配合EEMD算法完成最终的自适应滤波器设计,完成对工频干扰的滤除。仿真结果表明,经EEMD算法分解原始信号并搭配使用LMS算法构造的自适应滤波器在滤除不同相位和不同频率下的工频干扰有良好表现。
1 工频干扰的引入途径
最常引入的外界干扰信号即是市电的工频干扰,其根本原因是仪器电势与环境电势的差异[10]。产生电势差异来自以下三个方面:
(1)市电供电电器干扰。生活环境中的其他的日常电器都会产生交变电场,且空间重置大量电力线辐射。这些交变电场和空间电磁场都会产生相应工频干扰。
(2)检测仪器未良好接地。市电的地线与大地之间存在着接地阻抗,如果SEMG检测端单元与其他市电电源共用一个地,且市电没有规范布线和良好接地,电势差可达100~200 V。
(3)检测者本身。由于被检测者身体不可避免的处在空间各种电磁场之中,被检测者的身体受感应电磁场而产生感应电流,会同时将感应工频电流;进而噪声混入采集信号当中。
2 解决方法
2.1 前置放大电路的处理
在前置放大硬件电路上采用如下方法抑制工频干扰:
(1)在保证前级放大电路高增益的情况下,针对市电供电电器干扰,需将外界电磁场辐射屏蔽于检测设备之外。首先生理检测设备置于金属屏蔽盒内并良好接地,且前级放大电路应尽可能地靠近表贴电极,缩短检测电极与放大器之间的连线,并使用屏蔽电缆将放大单元与采集电极相连。
(2)在采集中采用隔离的方法,即使得SEMG采集设备与市电系统中没有任何通路。检测设备使用直流电压供电,干电池可作为选择。
(3)考虑到电池供电会使设备受到电池容量及工作时间的限制,因此若采用市电供电,必须利用光耦隔离,将市电供电单元与采集放大电路完全隔离开来。在某些文献中也研制出了带有放大功能的检测电极,也在部分研究中得到使用,具有一定抑制工频噪声的效果[11]。
(4)受试者本身引入的工频干扰由检测电极处引入,解决方法经研究为差分电极距离相隔大约为10 mm。由于距离电力线附近较远处干扰源产生的工频干扰在两个电极处的幅值基本相同,且由于SEMG检测设备基本采用差分运放,这对共模信号有很高的抑制作用,使得两电极上产生的相同的工频干扰可良好滤除。采集电路如图1所示。

图1 前置放大电路实现图
2.2 数字信号处理方法
2.2.1 数字滤波器的优点
数字滤波器是指输入/输出均为数字信号,通过一定运算关系改变输入信号所含频率成分的相对比例或滤除某些频率成分的器件。数字滤波器通常需要完成两步:一是完成专用的数字处理硬件;二是把滤波器所需的算法通过程序来运行。50 Hz数字陷波器的设计方法多种多样,采用软件编程的方法通常有:小波变换滤波、自适应滤波、匹配滤波等。数字滤波器与模拟滤波器相比较,具有精度高、稳定好、体积小、高灵活度、无需阻抗匹配等优点[12]。Matlab自带的信号处理工具箱,使得原本复杂的滤波器设计变得简化,已广泛地使用到各种滤波器的设计当中。
2.2.2 EMD
经验模式分解(EMD)是由华裔科学家 NE Huang首次提出的[13⁃14]。EMD是一种可对非线性信号及非平稳信号进行数据分析处理的算法,EMD分解方法是希尔伯特变换的重要组成部分,它能将信号分立在不同尺度,由此得到一系列本征模态函数(IMF)。这些IMF包含着数据最基本信息,且这些IMF是自适应的,因此在处理非平稳、非线性信号的处理研究中EMD有出色的处理能力。EMD算法使用数值变化过程,依据瞬时频率的必要条件,定义了一个本征模态函数必须满足的两个基本条件:
(1)整个信号段内,极值点的个数和过零点的个数相等,或仅相差不超过一个。
(2)任意时刻局部极大值和极小值点构成的包络线均值为零,即包络相对于时间轴对称。EMD算法假设对于任何信号都是由若干优先的本征模态函数组成,每一个本征模态函数通过如下方法[15]分解:
首先标记处原始信号的极大极小值,然后在原始信号x(t)上使用三次样条函数,得到极大值包络xu(n)和极小值包络x1(n)。将两包络值相减,得到包络均值:
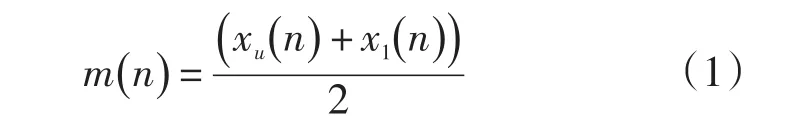
原信号序列x(n)减去m(n),得到一个去低频信号:

将h1()n 作为新数据,并重复式(1)、式(2)的过程,直至最终的信号满足IMF定义,即需满足式:

c1(n)包含有信号的高频分量,残余信号r1(n)则可由以下算式得出:
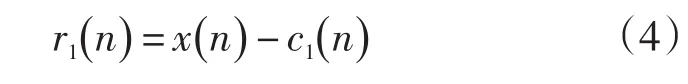
将r1(n )作为新数据并重复式(1)~式(4)的过程,直至抽取中所有的IMF分量。其中均值漂移过程在第m阶残余信号rm(n)小于预设值或是单调时停止。
x(n)经EMD分解后得到为:
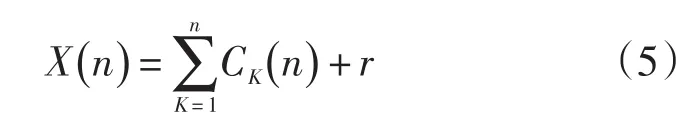
在实际情况下,上、下包络的均值无法为零,通常判断在满足式(6)时,就认为包络的均值已满足IMF均值为零的条件:

式中ε为筛分门限,取值为0.2~0.3。
2.2.3 EEMD
集合经验模式算法(Ensemble EMD,EEMD)是EMD算法的一种改进,旨在解决EMD算法中的尺度分立问题。EEMD作为一种噪声辅助分析方法,其由Z.Wa及N.E.Huang提出的[16]。EEMD的分解规则是给信号的整个尺度附加均匀白噪声,当信号附加均匀白噪声时,由于每个独立分量的噪声是不同的,因此当使用全体集合的均值时,噪声也会被滤除。EEMD分解方法可如下解释:
(1)为目标序列x(n)增加白噪声序列W(n),并将x(n)分解出IMF。
(2)多次使用不同的白噪声序列重复第(1)步,从所得IMF集合中找出最终的IMF。
2.2.4 基于EEMD算法及LMS算法的自适应滤波器的设计
自适应滤波器可在工频干扰频率改变时,跟随其改变自身频率。自适应滤波器通过可调整系数的滤波器将输入信号加权后产生一个输出,然后与期望的参考或训练信号进行比较,形成误差信号。这个误差信号修正可编程滤波器的权系数。自适应理论经过数十年的研究获得了极大的发展,根据不同的优化准则推导出许多不同的自适应理论。目前该理论主要包括以下几个分支[17]:基于维纳滤波器理论的最小均方算法、基于卡尔曼滤波理论的卡尔曼算法、基于最小二乘准则的算法、基于人工神经网络的方法。
美国斯坦福大学的Widrow于1960年提出了最小均方(LMS)算法[18]。LMS算法是一种运算量小、算法结构简单、算法稳健的自适应算法,自提出后得到广泛应用。LMS基于最小均方误差准则。当滤波器权系数进行迭代式,LMS算法会按一定比例沿着误差性能曲面的梯度估值的负方向更新。利用LMS算法设计自适应滤波器的流程为:首先选择参数:选择滤波器的抽头数及合适的步长(Step⁃Size);然后初始化,令滤波器的初始权值W(0)=0;最后计算误差信号。滤波器系列矢量估值W(n)、输入信号X(n)以及期望信号d(n),误差信号为:

计算滤波器权系数估值:
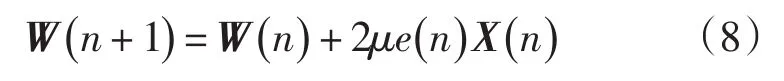
将时间指数n增加1,重复式(3)的过程,直至稳态。滤波器的流程图如图2所示。
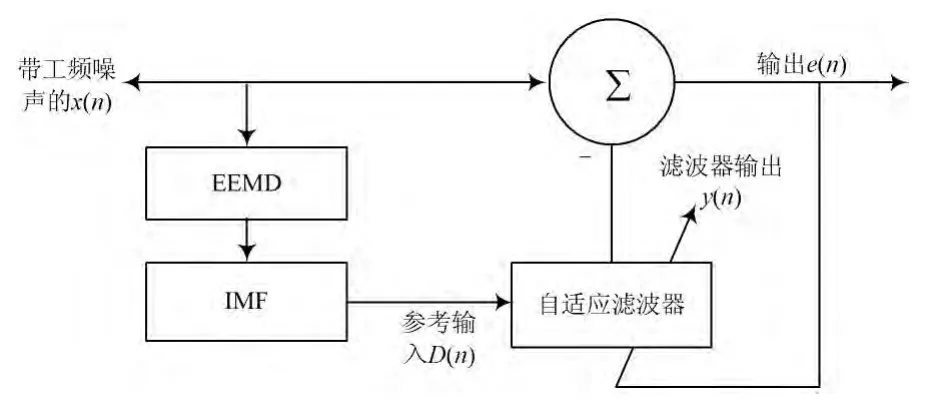
图2 EEMD算法自适应滤波器流程图
原始信号x(n)由EMD分解后,表示如下:
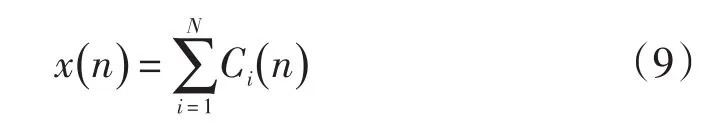
于是所构造的低通滤波器为:
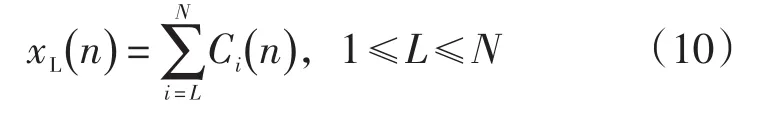
所构造的高通滤波器为:
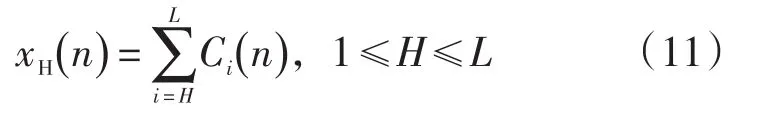
经EMD分解后的原始信号可由IMF选择重建,且将IMF作为自适应滤波的参考信号,使得滤波器能很好地跟随工频干扰频率的变化,达到抑制噪声的目的。
3 结果分析
为验证实验所设计的滤波器的效果,实验数据的来源为硬件电路采集人体前臂的SEMG信号,实验共3min,受试者做握拳和放松动作,每10 s切换一次。采集数据的采样率为1 000 Hz,采用5通道采集,并对采集波形进行叠加。得到含有工频干扰的原始肌电信号如图3所示。将各通道波形在时域上进行叠加,得到的叠加波形如图4所示。再将所叠加5通道SEMG信号输入基于EEMD算法的自适应滤波器后,经Matlab数据处理后得出滤除工频干扰噪声的信号如图5所示。
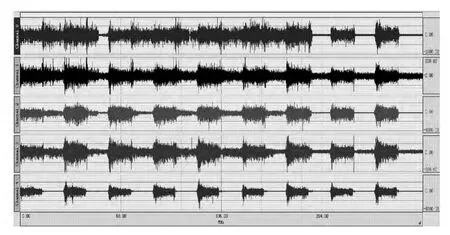
图3 5通道原始肌电信号

图4 含噪声的单通道肌电信号

图5 滤除工频干扰后的但同到肌电信号
从仿真结果可以看出,基于EEMD⁃LMS的自适应滤波器,对工频干扰有良好的抑制作用。不同于以往的数字滤波器,自适应滤波器对于不同相位不同频率的工频干扰都能跟随干扰频率的变化进行滤波。式(12)~式(14)分别给出了计算自适应滤波器的三个公式。

式中:x(n)为已滤除噪声的信号,x(n)表示重构的输出信号。
表2对基于EMD⁃LMS的自适应滤波器及基于EEMD⁃LMS的自适应滤波器的性能参数做出了对比。其结果是,EEMD⁃LMS具有在提高检测信号信噪比,均方根误差上都有良好的表现。

表2 基于不同算法的自适应滤波器性能对比
4 结语
本文提出了滤除肌电信号检测中的工频干扰的方法,在电路硬件方面采用屏蔽隔离的方式,使得环境中的市电干扰能最大程度降低。其次提出了一种基于EEMD⁃LMS算法的自适应滤波器进行对所采集信号的数字滤波。在仿真中可证明,基于EEMD算法与LMS算法的自适应滤波器在提高信号信噪比及减小均方误差方面均有较好的改善,且能够跟随相位或频率变化的的工频干扰进行针对性的滤除,此方法在进行生理信号采集中,能够准确的滤除工频噪声,可广泛使用于相关设计中。
[1]DE LUCA C J,GILMORE L D ,KUZNETSOV M,et al.Fil⁃tering the surface EMG signal:Movement artifact and baseline noise contamination[J].Journal of Biomechanics,2010,43:1573⁃1579.
[2]HUHTA JC,WEBSTER JG.60Hz intererence in electrocar⁃diography[J].IEEE Transactions on Biomed Engineering,1973,BME⁃20:91⁃101.
[3]鲁连刚.滤除50 Hz工频干扰的滤波电路设计[J].辽宁师专学报,2012,14(1):90⁃92.
[4]付聪,李强,李博.表面肌电信号采集与降噪处理[J].现代医学生物进展,2011,11(20):3951⁃3953.
[5]ACHARYA S,MUGLER D H,TAYLOR B C.A fast adaptive filter for electrocardiography[C]//Proceedings of the IEEE 30th Annual Northeast Bioengineering Conference.[S.1.]: IEEE,2004:106⁃107.
[6]袁婷婷.表面肌电信号处理和模式识别方法研究[D].武汉:武汉理工大学,2012.
[7]钱振华,宋汉文.经验模式分解方法(EMD)研究综述[C]//上海市国际工业博览会第三届上海市“工程与振动”科技论坛论文集.上海:“工程与振动”科技论坛,2005:118⁃119.
[8]WIDOW B,MCCOOL JM,KAUNITZ J,et al.Adaptive noise cancelling Principles and applications[J].IEEE Press,1975,63:1692⁃1716.
[9]王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学,2010.
[10]赵章琰.表面肌电信号检测和处理中若干关键技术研究[D].合肥:中国科学技术大学,2010.
[11]MANNABE H,SUGIMURA H A.A ring⁃shaped EMG mea⁃surement system for applying to user interface[J].Engi⁃neering in Medicine and Biology Society,2003,4:3020 ⁃3023.
[12]王蔚.Matlab环境下的数字滤波器设计及其应用[D].苏州:苏州大学,2002.
[13]HUANG N E.The empirical mode composition and the Hil⁃bert spectrum for nonlinear and non⁃stationary time series analysis[M].Great Britain:Royal Society,1998.
[14]HUANG N E.A new view of nonlinear water waves:the Hil⁃bert spectrum[J].Annu Rev Fluid Mech,1999,31:417⁃457.
[15]JENITTA J,RAJESWARIA.Denoising of ECG signal based on improved adaptive filter with EMD and EEMD[C]//2013 IEEE Conference on Information&Communication Technolo⁃gies(ICT).[S.1.]:IEEE,2013:957⁃962.
[16]WU Z,HUANG N E.Emsemble empirical mode decomposi⁃tion method and the Hilbert spectrum for non⁃stationary time series analysis[M].Great Britain:Royal Society,1998.
[17]张会先.自适应滤波算法的研究与应用[D].西安:西安电子科技大学,2012.
[18]MCCOOL W JM,LARIMORE M G,JOHNSON C R.Sta⁃tionary and nonstationary learning characteristics of the LMS adaptive filter[J].Proc IEEE,1976,64:1151⁃1161.

