基于刚度分配法的弯剪组合螺栓法兰设计探讨
沈兰华,范开英,孟庆琳
(山东丰汇设备技术有限公司,山东 济南 250200)
基于刚度分配法的弯剪组合螺栓法兰设计探讨
沈兰华,范开英,孟庆琳
(山东丰汇设备技术有限公司,山东 济南 250200)
[摘 要]分析了螺栓法兰连接的变形协调原则,提出了一种新的螺栓连接计算方法——刚度分配法,通过实例对法兰连接不同计算方法的结果进行比较,得到应按螺栓分布情况对螺栓和连接断面进行校核的结论,为工程实际中法兰连接设计校核提供借鉴。
[关键词]刚度分配法;螺栓法兰;连接设计;法兰计算
梁承受弯剪组合是一种常见的受力状态,桥机,门机的主梁,塔机的“十字梁”底架[1]都是典型的弯剪组合结构形式。梁分段处采用螺栓法兰连接、连接翼缘和腹板采用螺栓连接时的设计计算方法[2]有以下4种:a-等强度设计法,b-实用设计法,c-精确计算设计法,d-常用的简化设计法。
精确计算设计法应是其他设计方法简化的依据,其原理是按被连接的梁以翼缘和腹板各自分担作用于拼接连接处的弯矩M,并以梁翼缘承担弯矩MF,腹板同时承担弯矩MW和全部剪力P来拼接连接的设计,其弯矩分配按照梁翼缘板和腹杆惯性矩比例进行分配。这种方法的计算结论和常用的简化设计法有很大差异,特别是靠近翼缘板附近的螺栓按方法d计算时不参与梁的弯矩分配,但法c计算此部分产生的应力,两种方法设计出螺栓的大小和数量差异很大。
1 刚度分配法思想
连接法兰由螺栓群连接,梁(被螺栓孔削弱截面)受力应按照螺栓分布对梁受力的影响考虑,从应变的微观角度分析,连接法兰的变形由螺栓群的刚度决定。当螺栓群的实际布置刚度与梁自身的刚度不同时,梁局部位置承受的载荷为螺栓群传递的载荷,其设计应按螺栓载荷分配校核。
在梁受弯剪组合的作用下,计算的基本假定如下。
1)被连接的构件是绝对刚性的,而螺栓是弹性的,螺栓群的刚度与连接法兰无关。
2)被连接的构件绕螺栓群中心O相对转动,螺栓的应变只与位置有关。
2 螺栓载荷计算
梁法兰处的弯矩为M,剪力为P,根据上述基本假定便可以得到:每个螺栓应变的大小与其到中心的距离成正比。

各颗螺栓承受的载荷为

式中 K——螺栓群刚度系数阵;
li——单个螺栓到螺栓群中心O的距离;
Ai——单个螺栓的截面积。
参照螺栓群法兰计算公式[3],螺栓群承受的弯矩等于法兰的弯矩和

由式(2)和式(3)推导出

螺栓群的载荷刚度系数是个常值,与螺栓的分布位置和螺栓的大小有关。螺栓因弯矩产生的应力为
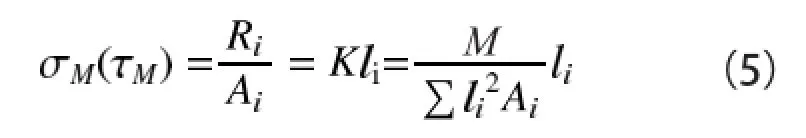
腹板上的螺栓是梁弯曲和梁剪切共同作用的结果。腹板螺栓水平分力由弯矩产生,垂直分力由剪力产生,假设腹板螺栓共有n个剪切面,腹板螺栓的合成应力为
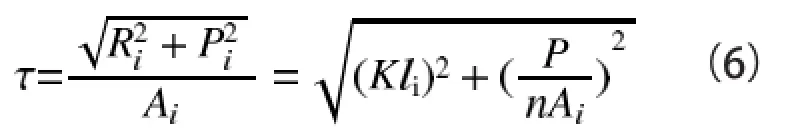
由式(4)可以看出螺栓群刚度K由全部螺栓决定,且离法兰距离越远的螺栓承载越大,当翼缘板螺栓数目较多时,特别是有多排螺栓时,腹板螺栓对刚度的承载比例很小,对腹板螺栓来讲,此值近似为定值。
由式(6)可以看出,由弯矩分配产生的应力为定值时,腹板螺栓受力只与剪应力有关。螺栓设计方法c算法是不精确的,当螺栓群刚度与梁刚度不一致时,载荷按照连接件分配,并不是由梁刚度决定。螺栓按方法d计算结果比实际偏小。
3 螺栓平法兰连接计算
翼缘板计算时按扣除孔后的强度计算[3],其应力分配不应从梁惯性矩考虑,而应考虑螺栓布置后螺栓群刚度与梁刚度的不同,计算螺栓强度对梁的应力影响。通常情况下,翼缘板的螺栓布置相对较多时,翼缘板的应力会有所增大,造成连接部位的应力集中。
3.1 对梁翼缘板的校核
根据螺栓的布置和被连接件的破坏形式,净截面积的计算有以下两种情况:螺栓并列布置时,构件在第一列钉孔处的截面最危险,构件可能与该净截面发生破坏;螺栓错列布置时,构件也可能沿锯齿状的净截面发生破坏,取决于螺栓行列间距和孔径大小[4]。
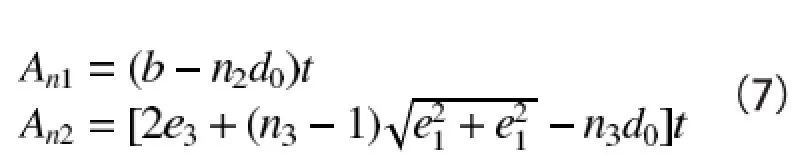
3.2 被孔削弱的连接件的强度计算
螺栓连接的构件强度按下式进行计算

式中 N——翼缘板螺栓载荷和;
Aj——构件净截面积,按式(6)计算。
4 实例计算
某桥机跨距30m,中间承受在100t,承受弯矩750tm,在梁中间设置连接法兰。法兰尺寸为800×1600×30×14,按照螺栓连接法计算翼缘板需要M30螺栓15.4颗。实际螺栓群布置是一般多布置10%,因此布置17颗;腹板螺栓布置15 颗M24螺栓,螺栓为8.8级精制螺栓,连接法兰为双剪力板构造。法兰连接螺栓布置形式如图1所示。
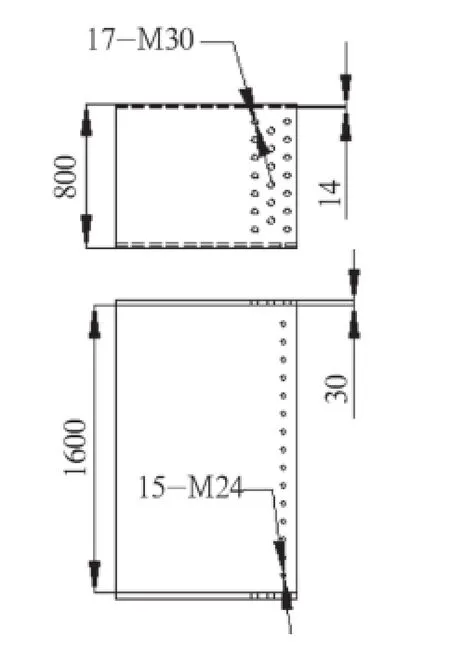
图1 连接法兰一
对此进行精确计算设计法和简化设计法进行比较,数据如表1。
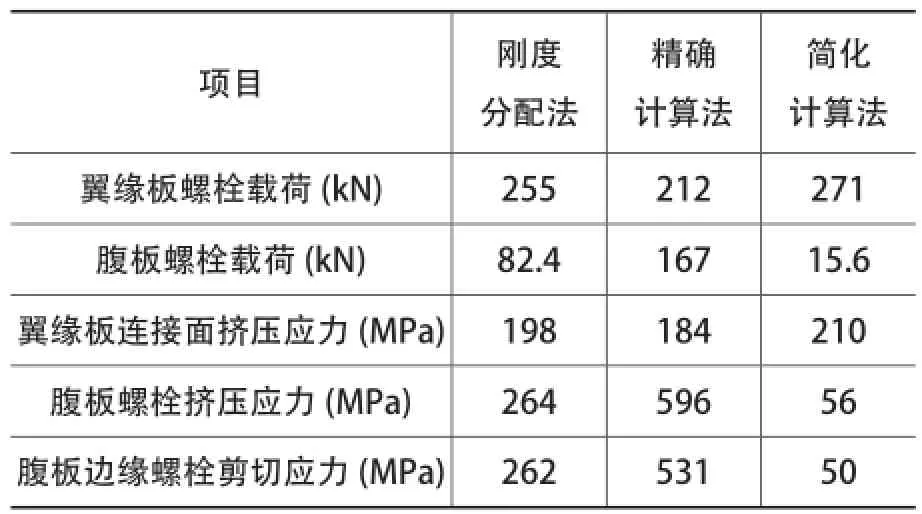
表1 法兰连接不同计算方法的结果比较
由表1中数据可以看出,选择不同的校核方法,会得出不同的结论,特别是腹板螺栓载荷差别非常大。精确计算法的结论腹板螺栓已经不满足要求,但实际上梁的变形从形心线开始往两端变形越来越大,腹板螺栓的变形要小于翼缘板螺栓变形,翼缘板的螺栓未发生塑性变形前,腹板的螺栓也不可能破坏。因此精确计算法的计算假设条件是有问题的,在法兰连接设计不应按此方法校核。
简化计算法与螺栓群刚度分配法比较发现,实际上腹板螺栓即使取小后,其分担弯矩的部分也会变小。通常情况下,梁腹板从边缘到中间的弯曲应力衰减比剪切应力增大的幅度要快,因此梁腹板只通过剪力校核就满足要求,这个经验同样适用于螺栓计算。因此在简化算法中,翼缘板螺栓承受所有弯矩,腹板螺栓也只承受剪力的计算方法是可行的。但简化计算法并不能反映真实的应力分布。
优化上述实例中连接方案,使螺栓大小更接近连接板厚,按翼缘板采用20颗M30螺栓,腹板采用15颗M16螺栓,如图2布置。优化结果如表2所示。
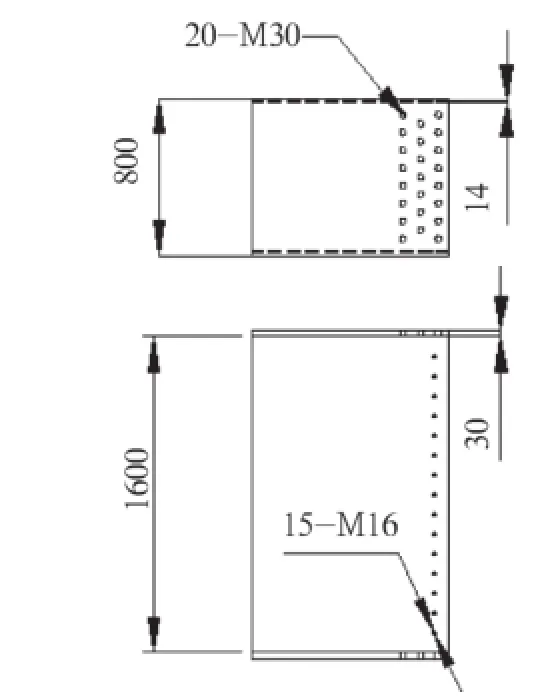
图2 连接法兰二
对比表1和表2结果可知:腹板螺栓受力因刚度分配发生了变化,实际腹板螺栓受力从82.4kN降到48.2kN,而简化计算法体现不出此变化;螺栓群整体刚度的增强时,螺栓应力应该降低,刚度分配法计算结果验证了这一点,而简化计算方法中的结果有所增加。综上所述,刚度分配法比简化计算法更符合实际情况。
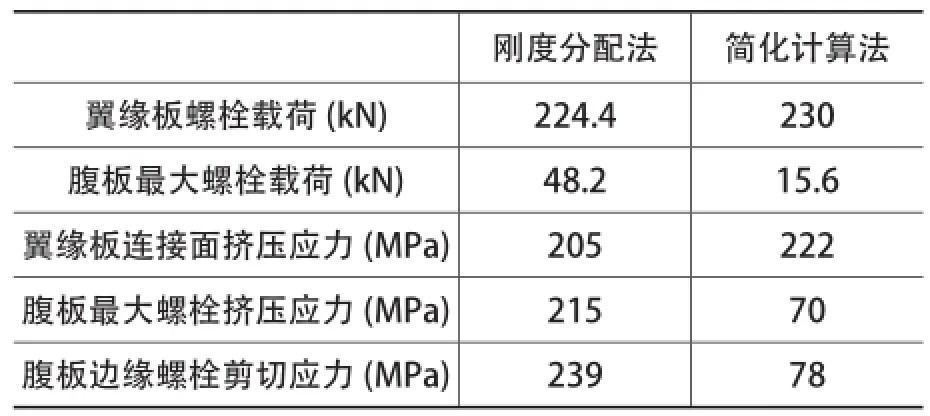
表2 连接法兰优化方案的结果对比
5 结 论
本文总结分析以往螺栓群的计算原则和假设条件,提出了梁法兰连接计算的螺栓群刚度分配法。
1)螺栓的刚度矩阵分配决定了连接断面的应力分布,而不是连接断面的惯性矩决定了螺栓的载荷大小,精确计算设计法的假设条件有误,因此造成了与实际设计结论的矛盾。
2)简化计算方法和实际情况相比较:翼缘板略有保守,但误差小于3%;腹板螺栓受力偏差较大。实际布置时应适当留有余量,一般螺栓数量比简化计算数目多10%即可满足要求。
3)腹板螺栓的应力与腹板的惯性矩并无直接的联系,此部分载荷并不固定,可根据刚度分配法计算。腹板螺栓承受梁弯曲引起的载荷应力基本固定,与面积关系较小,剪应力与面积有关,是腹板螺栓的主要计算依据。
[参考文献]
[1] 孟庆琳,史海红,沈兰华,等.塔机“十字梁”底座设计计算方法研究[J].建筑机械化,2013,(6):50-51.
[2] 李和华.钢结构连接节点设计手册(第二版)[M].北京:中国建筑工业出版社,2005.
[3] 张志文.起重机设计手册(第一版)[M].北京:中国铁道出版社,2001.
[4] 陈玮璋.起重机械金属结构[M].北京:人民交通出版社,1986.
(编辑 贾泽辉)
Design and discussion of base on rigidity distribution method bending shear combination bolt fl ange
SHEN Lan-hua, FAN Kai-ying, MENG Qing-lin
[中图分类号]TH131.3
[文献标识码]B
[文章编号]1001-1366(2015)06-0042-03
[收稿日期]2015-03-14

