纳米压印的模拟方法研究进展

万萍

摘 要：本文分别从模型构造和模拟方法上介绍了黏弹性牛顿流体模型、分子动力学模型、质点动力学模型和气泡挤压模型等四种模拟方法。并基于有限元分析方法借助于ANSYS Workbench软件对纳米压印过程中二维的胶体流动变形过程进行模拟分析。胶体在进行流动变形时，采用Mooney-Rivlin模型表征胶体的机械性能，并使用非线性超弹性材料模型进行建模求解。

关键词：胶体流动；弹性牛顿流体模型；Mooney-Riviln模型；纳米压印；模拟方法

中图分类号：TG58 文献标识码：A

1 引言

较早的纳米压印模拟是把高分子聚合物作为黏弹性牛顿流体或者非线性弹性固体。非线性弹性固体模型是用市场上可以买到的MARC程序所编辑的Moony-Rivlin模型，依靠有限元法和矩阵平面应变原理，在玻璃化转变温度以上的时候将聚合物模拟成弹性橡胶。黏弹性牛顿流体模型是运用商业计算流体动力学软件CFD-ACE，运用有限体积理论，在欧拉网格的基础上运用流体体积函数（VOF）理论来追踪聚合物边界的变形情况。

2 四种模拟方法

2.1 黏弹性牛顿流体模型

黏弹性流体模型有很多类，最为常用的是流体体积函数（VOF）模型：把函数定义为目标流体的体积与网格体积的比值，通过该函数在每个网格上的值就可以实现对运动界面的追踪。自由边界或者可移动边界理论GOMA模型是在拉格朗日欧拉耦合（ALE）坐标系下对流体聚合物和固体压印模进行分别建模，从而使流体聚合物与固体压印模在运动过中能够相互独立，以此来实现大的边界自由变形运动。

2.2 分子动力学模型

该有限元模型包括压印模、聚合物和镍基板三个部分。该模型中，氢原子附着于每个氧原子表面，它们之间仅用一个硅原子作为连接在一起。聚合物由64 PMMA非晶态分子组成，每个颗粒物的分子量为10016（每个聚合物的分子量为100）。基板则有4层镍原子组成，它们在垂直方向呈FCC结构。由于压印模和基板的杨氏模量远大于PMMA，所以将压印模和基板假设为刚体。在镍原子的垂直方向施加固定约束用以限制镍基板垂直方向的位移。

2.3 质点动力学模型

在多尺度仿真模型中，将原子论和连续模型理论结合起来用以描述材料的特性，在大部分多尺度理论中，原子论是用来处理大变形问题而连续理论却很少用于大变形问题的研究。将最小单位假设为晶格主要有以下优点：晶格很适合于描述固体材料，可以通过观察晶格尺寸的不同来了解整个模型的变化情况，更为重要的是，使用晶格最为最小单元，平衡准则很容易确立。

2.4 气泡挤压模型

聚合物被放置在基板上，预先被刻有图案的压印模通过外力作用压放到涂有聚合物的基板上，聚合物受到压印模和基板的挤压而向周围流动，聚合物以一个速率从左边向右边移动。当聚合物的表面接触到空腔边缘时，聚合物被分割为两部分，一部分继续往右边流动，另一部分开始填充空腔，空腔中的气体开始受到挤压，随着空腔长度的增加，聚合物在下部分离开空腔之间已经达到了空腔的顶端，因此，聚合物在这种情况下并没有分流，并不会有气体留在空腔中，气泡的产生与空腔的尺寸相关。

3 有限元分析

3.1 几何模型的建立

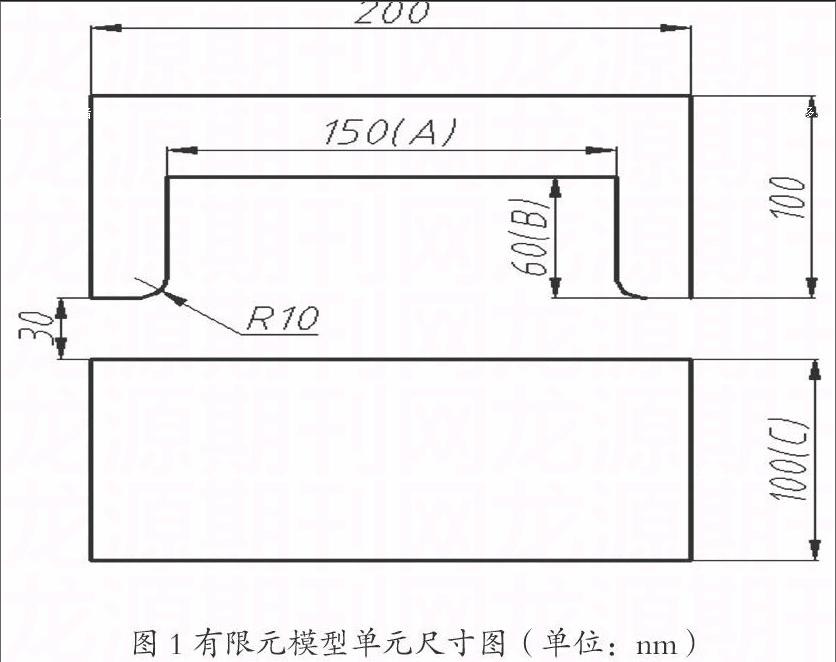
为了简化模型，增加计算速度，将基板、聚合物与压印模三者直接的作用关系直接简化为压印模与聚合物之间相互作用，而基板与聚合物之间的相互作用简化为聚合物底部的Y方向位移为0。在纳米压印过程中，3D压印模可以简化为2D结构，横向以模型为基础单元向左右方向扩展，纵向则以图中平面向前后延伸，具体尺寸如图1所示，图1中尺寸A、B、C为关键尺寸，它们的变化将直接影响压印过程。

3.2 有限元模型求解

纳米压印过程采用Static Structure（静力学）模块进行求解分析，主要包括模型材料参数的赋予、接触设置、网格划分、求解设置、施加载荷与约束和模型求解这6个阶段。

3.3 有限元模型后处理

本模型的后处理主要是研究压印模的位移与外载荷之间的关系，从而得出在外载荷的作用下聚合物流动的过程。包括对模型的Total Deformation（总体变形）、Equivalent Stress（等效应力）、X方向Deformation（变形）、Y方向Deformation（变形）做具体分析。

（1）总体变形

纳米压印过程中中，聚合物受到压印模的作用产生较大的形变从而填满压印模的空腔实现图形的转移，在不同时间不同外载荷作用下，聚合物受到压印模两端凸起处挤压力的作用，两端的胶体逐渐向空腔内部流动，最终填充满整个空腔。

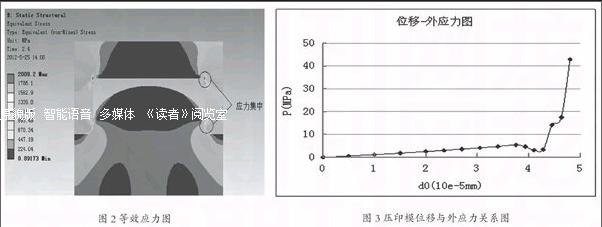
（2）等效应力

如图2所示，压印模在外载荷的作用下与聚合物相互作用产生内应力。由于本模型是通过位移加载，而本文需要研究外应力载荷与聚合物的形变之间的相互关系，因此通过将压印模中间的最小应力等效为对压印模所施加的外应力，通过以上转换可以表示出压印模的位移与外载荷作用应力之间的相互关系，图3中d表示压印模的实际位移，d0表示从压印模接触聚合物开始后的接触位移，P表示外载荷，从图2中可以看出，外应力的变化可以分为两个阶段，初始的线性阶段和非线性阶段，初始的线性阶段是聚合物凸起处未接触到空腔的顶端阶段，非线性阶段是聚合物凸起接触到空腔之后的阶段，这两个阶段转变处外应力的大小有较为明显的变化，当聚合物接触到空腔顶端之后，需要较大的外应力作用使其发生更大的变形。

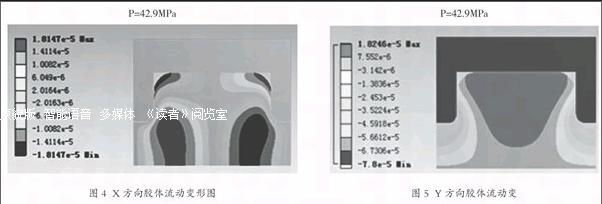
（3）X方向和Y方向变形

当胶体受到压印模的挤压力之后将会产生X方向和Y方向的弹性形变（流动）。图4为在不同时刻、不同外载荷力的作用下胶体在X方向上的弹性形变，受到压印模两端凸起作用，胶体内部下半部分向内收敛，而顶端处则向外扩散，右半部分形成顺时针流动，左半部分形成逆时针流动，从而达到胶体填充整个空腔的过程。图5为在不同时刻、不同外载荷力作用下胶体在Y方向上的弹性变形，受压印模两端凸起的作用，胶体左右两端向下流动，而中间部分则向上凸起，与X方向变形相似，右半部分形成顺时针流动，左半部分形成逆时针流动。

结语

对现有的纳米压印模拟方法：黏弹性牛顿流体模型、分子动力学模型、质点动力学模型、气泡挤压模型、非线性超弹性模型等进行分析讨论，逐一介绍它们的建模理论与方法。重点对非线性超弹性模型通过ANSYS Workbench建立有限元模型分别从压印模几何尺寸（空腔宽度与高度）和胶体厚度两个方面对纳米压印过程中胶体流动情况进行了研究。

参考文献

[1] Harry D Rowland， Amy C Sun， P Randy Schunk and William P King. Impact of polymer film thickness and cavity size on polymer flow during embossing： toward process design rules for nanoimprint lithography. Journal of Micromechanics and Microengineering. 2005， 11.

[2] Chih-Wei Hsieh and Cheng-Kuo Sung. Atomic-Scale Friction in Direct Imprinting Process： Molecular Dynamics Simulation.Japanese Journal of Applied Physics.2007.9.20.

[3] Te-Hua Fang， Cheng-Da Wu， Win-Jin Chang and Sung-Shui Chi. Effect of thermal annealing on nanoimprinted Cu–Ni alloys using molecular dynamics simulation. Applied Surface Science.2009.1.

[4] Cheng-Da Wu and Jen-Fin Lin.Multiscale particle dynamics in nanoimprint process. Applied Physics A. 2008.2.15.

[5] Daisuke Morihara， Hiroshi Hiroshima and Yoshihiko Hirai. Numerical study on bubble trapping in UV-nanoimprint lithography. Mocroelectronic Engineering. 2008.12.13.