2015年高考北京卷数学（理科）压轴题的背景是数学黑洞问题

1  2015年高考北京卷数学（理科）压轴题及其参考答案

高考题1 （2015年高考北京卷数学（理科）第20题）已知数列{an}满足：a1∈N*，a1≤36，且an+1=2an （an≤18）

2an-36 （an>18）（n=1，2，…）.记集合M={an|n∈N*}.

（Ⅰ）若a1=6，写出集合M的所有元素;

（Ⅱ）若集合M存在一个元素是3的倍数，证明：M的所有元素都是3的倍数;

（Ⅲ）求集合M的元素个数的最大值.

参考答案 （Ⅰ）当a1=6时，由所给的递推式可得数列{an}：6，12，24，12，24，…，所以M={6，12，24}，即集合M的所有元素分别是6，12，24.

（Ⅱ）假设a1不是3的倍数，由所给的递推式及数学归纳法可得an（n∈N*）均不是3的倍数.这与题设相矛盾！所以a1是3的倍数.再由所给的递推式及数学归纳法可得an（n∈N*）均是3的倍数，即M的所有元素都是3的倍数.

（Ⅲ）用数学归纳法易证an≤36（n∈N*）.

易知a2是偶数，再用数学归纳法易证an（n∈N*，n≥3）是4的倍数.

由所给的递推式可得，an+1与2an（n∈N*）被9除所得的余数相等.

①若数列{an}的项中有3的倍数，则由（Ⅱ）的结论知，an（n∈N*）均是3的倍数.所以a1被9除所得的余数是0，3，或6.

由此可得数列{an}的项被9除所得的余数依次为0，0，…;或3，6，3，6，…;或6，3，6，3，….

在不大于36的正整数中：被9除余0且是4的倍数的只有36，被9除余3且是4的倍数的数只有12，被9除余6且是4的倍数的数只有24.

所以数列{an}的项从第3项开始必呈现周期性变化，且周期是1或2.

得此时集合M的元素个数至多是2+2=4.

②若数列{an}的项均不是3的倍数，则a3被9除所得的余数只可能是1，4，7，2，5，8.再由递推式可得，数列{an}的项从第3项起被9除所得的余数呈现周期性变化，且周期分别是1，2，4，8，7，5;4，8，7，5，1，2;7，5，1，2，4，8;2，4，8，7，5，1;5，1，2，4，8，7;8，7，5，1，2，4.

又呈现周期性变化的每个数都是4的倍数且不大于36，所以1，2，4，8，7，5对应的数分别是28，20，4，8，16，32.

得此时集合M的元素个数至多是2+6=8.

又当a1=1时，可得M={1，2，4，8，16，32，28，20}，所以集合M的元素个数是8.

综上所述，可得集合M的元素个数的最大值是8.

注 笔者再给出第（Ⅱ）问的数学归纳法证明：

设集合M中的元素ak（k是确定的正整数）是3的倍数，则

①由所给的递推式及数学归纳法可得an（n∈N*，n≥k）均是3的倍数;

②由所给的递推式及反向数学归纳法可得an（n∈N*，n≤k）均是3的倍数.

所以an（n∈N*）均是3的倍数，即M的所有元素都是3的倍数.

2 用列举法解答2015年高考北京卷数学（理科）压轴题（即高考题1）

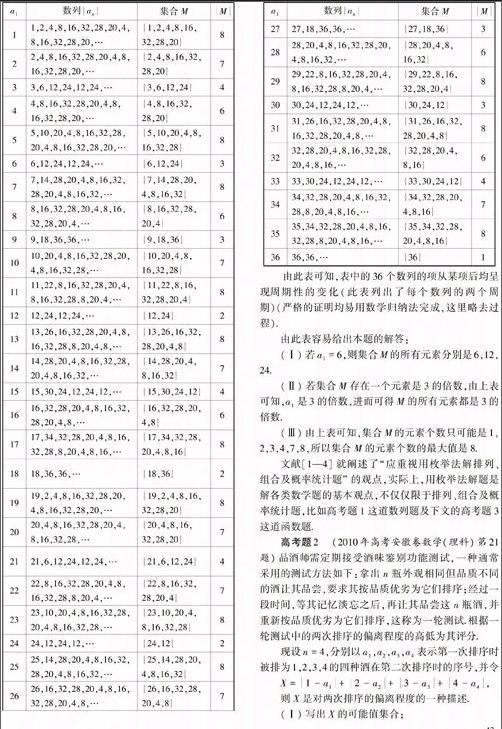
由题设可列举出满足题意的数列共36个（下表中的“M”表示“集合M的元素个数”）：

a1数列{an}集合MM

11，2，4，8，16，32，28，20，4，8，16，32，28，20，…{1，2，4，8，16，32，28，20}8

22，4，8，16，32，28，20，4，8，16，32，28，20，…{2，4，8，16，32，28，20}7

33，6，12，24，12，24，…{3，6，12，24}4

44，8，16，32，28，20，4，8，16，32，28，20，…{4，8，16，32，28，20}6

55，10，20，4，8，16，32，28，20，4，8，16，32，28，20，…{5，10，20，4，8，16，32，28}8

66，12，24，12，24，…{6，12，24}3

77，14，28，20，4，8，16，32，28，20，4，8，16，32，…{7，14，28，20，4，8，16，32}8

88，16，32，28，20，4，8，16，32，28，20，4，…{8，16，32，28，20，4}6

99，18，36，36，…{9，18，36}3

1010，20，4，8，16，32，28，20，4，8，16，32，28，…{10，20，4，8，16，32，28}7

1111，22，8，16，32，28，20，4，8，16，32，28，8，20，4，…{11，22，8，16，32，28，20，4}8

1212，24，12，24，…{12，24}2

1313，26，16，32，28，20，4，8，16，32，28，8，20，4，8，…{13，26，16，32，28，20，4，8}8

1414，28，20，4，8，16，32，28，20，4，8，16，32，…{14，28，20，4，8，16，32}7

1515，30，24，12，24，12，…{15，30，24，12}4

1616，32，28，20，4，8，16，32，28，20，4，8，…{16，32，28，20，4，8}6

1717，34，32，28，20，4，8，16，32，28，8，20，4，8，16，…{17，34，32，28，20，4，8，16}8

1818，36，36，…{18，36}2

1919，2，4，8，16，32，28，20，4，8，16，32，28，20，…{19，2，4，8，16，32，28，20}8

2020，4，8，16，32，28，20，4，8，16，32，28，…{20，4，8，16，32，28，20}7

2121，6，12，24，12，24，…{21，6，12，24}4

2222，8，16，32，28，20，4，8，16，32，28，8，20，4，…{22，8，16，32，28，20，4}7

2323，10，20，4，8，16，32，28，20，4，8，16，32，28，…{23，10，20，4，8，16，32，28}8

2424，12，24，12，…{24，12}2

2525，14，28，20，4，8，16，32，28，20，4，8，16，32，…{25，14，28，20，4，8，16，32}8

2626，16，32，28，20，4，8，16，32，28，20，4，8，…{26，16，32，28，20，4，8}7

2727，18，36，36，…{27，18，36}3

2828，20，4，8，16，32，28，20，4，8，16，32，…{28，20，4，8，16，32}6

2929，22，8，16，32，28，20，4，8，16，32，28，8，20，4，…{29，22，8，16，32，28，20，4}8

3030，24，12，24，12，…{30，24，12}3

3131，26，16，32，28，20，4，8，16，32，28，20，4，8，…{31，26，16，32，28，20，4，8}8

3232，28，20，4，8，16，32，28，20，4，8，16，…{32，28，20，4，8，16}6

3333，30，24，12，24，12，…{33，30，24，12}4

3434，32，28，20，4，8，16，32，28，8，20，4，8，16，…{34，32，28，20，4，8，16}7

3535，34，32，28，20，4，8，16，32，28，8，20，4，8，16，…{35，34，32，28，20，4，8，16}8

3636，36，…{36}1

由此表可知，表中的36个数列的项从某项后均呈现周期性的变化（此表列出了每个数列的两个周期）（严格的证明均易用数学归纳法完成，这里略去过程）.

由此表容易给出本题的解答：

（Ⅰ）若a1=6，则集合M的所有元素分别是6，12，24.

（Ⅱ）若集合M存在一个元素是3的倍数，由上表可知，a1是3的倍数，进而可得M的所有元素都是3的倍数.

（Ⅲ）由上表可知，集合M的元素个数只可能是1，2，3，4，7，8，所以集合M的元素个数的最大值是8.

文献[1—4]就阐述了“应重视用枚举法解排列、组合及概率统计题”的观点，实际上，用枚举法解题是解各类数学题的基本观点，不仅仅限于排列、组合及概率统计题，比如高考题1这道数列题及下文的高考题3这道函数题.

高考题2  （2010年高考安徽卷数学（理科）第21题）品酒师需定期接受酒味鉴别功能测试，一种通常采用的测试方法如下：拿出n瓶外观相同但品质不同的酒让其品尝，要求其按品质优劣为它们排序;经过一段时间，等其记忆淡忘之后，再让其品尝这n瓶酒，并重新按品质优劣为它们排序，这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.

现设n=4，分别以a1，a2，a3，a4表示第一次排序时被排为1，2，3，4的四种酒在第二次排序时的序号，并令

X=1-a1+2-a2+3-a3+4-a4，

则X是对两次排序的偏离程度的一种描述.

（Ⅰ）写出X的可能值集合;

（Ⅱ）假设a1，a2，a3，a4等可能地为1，2，3，4的各种排列，求X的分布列;

（Ⅲ）某品酒师在相继进行的三轮测试中，都有X≤2，

①试按（Ⅱ）中的结果，计算出现这种现象的概率（假定各轮测试相互独立）;

②你认为该品酒师的酒味鉴别功能如何？说明理由.

笔者在文献[1-4]中均用枚举法给出了这道题的解法：这里的一次试验是“将1，2，3，4排序”，先枚举出这A44=24种排列及其对应的X值，而后就很好求解各问了.

注 从阅卷情况看，这道高考压轴题的得分率极低.笔者认为造成这种情形的主要原因是考生不会用最简单的原始方法——枚举法解决计数问题，只知道套用排列组合公式解决复杂的计数问题，殊不知，用简单的枚举法也能轻松解决计数以及概率统计问题.

在解决某些数学题特别是排列组合及概率统计等与计数有关的问题时，有不少读者认为枚举法是“最烦、最繁、最差、最没有技术含量”的.其实不然：第一，当基本事件总数较少但情况又稍复杂时，枚举法一清二楚;枚举法应当是解这类题时首先想到的方法，比如树形图、列表法等;第三，即使枚举法失败，也可由此发现部分规律，对解题也有帮助.因此，解决某些数学题特别是计数问题时，应重视枚举法.

高考题3 （2012年高考新课标全国卷数学（文科）第21题）设函数f（x）=ex-ax-2.

（Ⅰ）求f（x）的单调区间;

（Ⅱ）若a=1，k为整数，且当x>0时，（x-k）f′（x）+x+1>0，求k的最大值.

解 （Ⅰ）略.

（Ⅱ）可得题设即xex-kex+k+1>0（x>0）恒成立.

由x=1时成立，得k<2e-1+1，所以整数k≤2.还可证k=2时成立：

设g（x）=xex-kex+k+1（x>0），

因为g′（x）=（x-1）ex（x>0），所以g（x）min=g（1）=3-e>0.

所以所求k的最大值是2.

注 由此解法还可得：整数k的取值范围是{不大于2的整数}，实数k的取值范围是（-∞，k0），其中k0是方程ek0-1=k0+1的正数解.

3 2015年高考北京卷数学（理科）压轴题（即高考题1）的背景是数学黑洞问题

先给出数学黑洞的有关概念及其记号、结论[5，6].

设有限集合（无限集合）A的所有元素x1，x2，…，xn（x1，x2，…，xn，…）可以按照某种规则排序为x1<x2<…<xn（x1<x2<…<xn<…）（这里“<”表示排序后的先后关系），f是集合A的变换，用“xi→xj”表示“f（xi）=xj”.

对xi重复作变换f（其中f0（xi）=xi，f1（xi）=f（xi）;由“变换”知，j∈N，fj（xi）∈A：

f0（xi）→f1（xi）→…→fs-1（xi）→fs（xi）→…→fs+n（xi）→…

若fs+n（xi）=fs（xi），s是满足此变换的最小自然数，n是满足此变换的最小正整数（此时，把fs（xi）→…→fs+n（xi）叫做集合A的变换f的由xi生成的第一个周期节），则fs（xi）→…→fs+n-1（xi）或fs+1（xi）→…→fs+n（xi）等等都叫做集合A的变换f的由xi生成的黑洞（共有n种书写形式，把这n种书写形式视作同一个黑洞），当然也可以看作集合A的变换f的由fj（xi）（j=0，1，…，s+n-1）生成的黑洞（因为对fj（xi）（j=0，1，…，s+n-1）连续作变换f均可生成以上周期节），f0（xi），f1（xi），…，fs-1（xi）的个数s叫做xi到集合A的变换f的黑洞fs（xi）→…→fs+n-1（xi）（该黑洞共有n种书写形式）的路程，简称黑程，记作h（xi）=s.

若仅能由集合A的元素xk1，xk2，…（其中xk1<xk2<…）生成上述黑洞，则把这个黑洞叫做集合A的变换f的第k1个黑洞，记作Dk1=fs（xi）→…→fs+n-1（xi），fs（xi），…，fs+n-1（xi）的个数n叫做集合A的变换f的第k1个黑洞Dk1的周长.

把集合A的变换f的黑洞的集合记作fA，把集合fA的元素个数fA记作H，所以fA={D1，D2，…，DH}.

研究集合A的变换f的黑洞，就是要研究黑洞的存在性，求出黑洞的个数H，求出集合fA，黑洞D1，D2，…，DH分别是由集合A的哪些元素生成的，每个元素的黑程各是多少？

定理1 若f是集合A的一个变换，x∈A，则由x可生成集合A的变换f的黑洞的充要条件是：存在仅与x有关（即与j无关）的常数a（x），j∈N，fj（x）≤a（x）.

证明 必要性.对x重复作变换f：

f0（x）→f1（x）→…→fs-1（x）→fs（x）→…→fs+n（x）→…

因为由x可生成集合A的变换f的黑洞，所以存在最小的自然数s和最小的正整数n，使fs+n（x）=fs（x），得j∈N，fj（x）≤max{f0（x），f1（x），…，fs+n-1（x）}.

选a（x）=max{f0（x），f1（x），…，fs+n-1（x）}，即得欲证成立.

充分性.因为j∈N，fj（x）≤a（x），所以对x重复作变换f：

x→f（x）→f2（x）→…

此变换可一直进行下去，而变换中的各数只能取有限个值，所以存在最小的自然数s和最小的正整数n，使fs+n（x）=fs（x）.

此时fs（x）→…→fs+n-1（x）就是由x生成的集合A的变换f的黑洞.

推论 若f是有限集合A的一个变换，则x∈A，由x可生成集合A的变换f的黑洞.

在高考题1中，设an+1=f（an）（n∈N*），可得f是有限集合A={1，2，3，…，36}的一个变换，所以由推论知，x∈A，由x可生成集合A的变换f的黑洞.

高考题1第（Ⅲ）问即求由集合A的元素生成的黑洞的黑程及该黑洞的周长之和的最大值.

图1高考题4 （2014年高考湖北卷数学（理科）第13题）设a是一个各位数字都不是0且没有重复数字的三位数，将组成a的3个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a）（例如a=815，I（a）=158，D（a）=851）.阅读如图1所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b=    .

答案：495.

文献[4]，[7]均指出了这道高考题的背景也是数学黑洞问题.

4 对2015年高考北京卷数学（理科）压轴题的推广

定理2 设常数p，k，l满足p是奇素数，k，l∈N.若数列{an}满足an+1=2an （an≤2kpl）

2an-2k+1pl （an>2kpl）（n∈N*），a1∈N*，a1≤2k+1pl，记M={an|n∈N*}，用M表示集合M元素的个数，则当a1变化时，有以下结论成立：

（1）an≤2k+1pl（n∈N*），2k+1ak+2;

（2）Mmin=1，且当a1=2k+1pl时M={2k+1pl};

（3）当l=0时，Mmax=k+2，且当a1=1时M=k+2;

（4）当（k，l，p）=（0，1，3），（0，1，5），（0，2，3）时Mmax=（p-1）pl-1+1，且当a1=1时M=（p-1）pl-1+1;

（5）当（p，l）=（3，1），（3，2），或（5，1）时Mmax=（p-1）pl-1+k+1，且当a1=1时M=（p-1）pl-1+k+1.

证明 （1）对n用数学归纳法，可证得an≤2k+1pl（n∈N*）;对m用数学归纳法，可证得2mam+1（m=0，1，2，…，k+1），所以2k+1ak+2.

（2）略.

（3）由结论（1）得ak+2≤2k+1，2k+1ak+2，所以ak+2=2k+1.进而可得an=2k+1（n≥k+2），所以M≤2k+1.

又当a1=1时，数列{an}：1，2，22，…，2k+1，2k+1，2k+1，…，所以M={1，2，22，…，2k+1}，M=k+2.

所以欲证结论成立.

（4）用本文第2节开头的列举法易证.

（5）①当（p，l）=（3，1）时，由结论（1）得ak+2≤3·2k+1，2k+1ak+2，所以ak+2=2k+1，2k+2，或3·2k+1.

当ak+2=2k+1时，可得数列{an}n≥k+2：2k+1，2k+2，2k+1，2k+2，…，所以M≤k+3.

当ak+2=2k+2时，可得数列{an}n≥k+2：2k+2，2k+1，2k+2，2k+1，…，所以M≤k+3.

当ak+2=3·2k+1时，可得an=3·2k+1（n≥k+2），所以M≤k+2.

总之，M≤k+3.

又当a1=1时，数列{an}：1，2，22，…，2k+1，2k+2，2k+1，2k+2，…，所以M={1，2，22，…，2k+2}，M=k+3.

所以此时欲证结论成立.

②当（p，l）=（3，2）时，由结论（1）得ak+2≤9·2k+1，2k+1ak+2，所以ak+2=i·2k+1（i=1，2，3，…，或9）.

同①可证得此时欲证结论也成立.

③同②可证.

问题 在定理2的题设下，求Mmax.

猜想 若定理2的题设满足，则当l∈N*时Mmax=（p-1）pl-1+k+1，且当a1=1时M=（p-1）pl-1+k+1.

参考文献

[1] 甘志国.善用枚举法解排列、组合及概率统计题[J].数学教学通讯（数学金刊·高考），

2015（2）：34-36.

[2] 甘志国.应重视用枚举法解概率题[J].中学数学，2012（3上）：42.

[3] 甘志国.立体几何与组合[M].哈尔滨：哈尔滨工业大学出版社，2014：151-159.

[4] 甘志国.高考数学真题解密[M].北京：清华大学出版社，2015.

[5] 甘志国.缩小变换黑洞[J].高等函授学报（自然科学版），1997（4）：56-59.

[6] 甘志国.初等数学研究[M].哈尔滨：哈尔滨工业大学出版社，2009：10-15.

[7] 甘志国.简介数学黑洞问题[J].数学通讯，2014（10上）：43-44.