考虑非线性系泊力TrussSpar平台耦合运动分析

， ，

(1. 上海船舶研究设计院，上海 201203; 2.大连理工大学 船舶工程学院， 辽宁 大连 116024;3.新加坡国立大学， 新加坡 118426)

考虑非线性系泊力TrussSpar平台耦合运动分析

张良1，李红霞2，毋晓妮3

(1.上海船舶研究设计院，上海201203; 2.大连理工大学船舶工程学院，辽宁大连116024;3.新加坡国立大学，新加坡118426)

TrussSpar广泛地应用于深水和超深水的海洋石油开发中，研究它的运动性能非常有必要。该文研究规则波浪下TrussSpar平台垂荡、横摇以及纵摇耦合6自由度运动特性。考虑平台垂荡频率与纵摇频率的2:1共振关系，采用龙格库塔法求解平台在非线性系泊力下平台的非线性运动响应。同时，考虑瞬时波面升高影响，研究非线性系泊力对平台运动的影响。计算结果表明：TrussSpar平台在考虑系泊力后，纵荡与纵摇响应幅值发生跳跃的临界波高值增大，延缓了跳跃现象的发生，但是不能阻止内共振情况的发生。同时，发现考虑瞬时波面升高影响，平台纵荡与纵摇响应幅值发生跳跃时的临界波高值减小，平台越容易发生内共振现象。考虑瞬时波面升高将导致平台的相对垂荡运动增大，引起平台干舷的剧烈变化，对平台的安全造成影响。

TrussSpar；非线性系泊力；波面升高；耦合运动；内共振

0 引言

Spar平台在深水和超深水的海洋石油勘探和开发中的应用越来越广泛,到目前为止，已经发展了四代Spar平台，其中Classic Spar和Truss Spar应用最广。Classic Spar平台主体是一个大直径、大吃水且具有规则外形的圆柱式浮筒结构，即使在恶劣的海况下，也能表现出优良的运动性能。但是，在某些海域，如中国南海，深海潜流将对巨大的圆柱体产生很大的拖曳力，在这种情况下，Truss Spar将是很有吸引力的一种选择[1]，当不需要储存大量原油时，Truss Spar具有最有效的结构形式。Downie等指出相对Classic Spar平台，Truss Spar平台具有很多优点，例如低建造费用，由于小拖曳面积而减小的系泊力以及对涡激振动不敏感等[2]。

在最近十多年里，针对Spar平台的运动和系泊分析的数值方法已经得到很大的发展和提高。这其中, Mekha[3], Ran and Kim[4], Ma Wei[5]发展了Spar平台运动分析的计算方法，并且研究了Spar平台运动的非线性特性。Tahar等[6]计算了设计水深为6000英尺的Classic Spar平台主体与立管的非线性耦合动力响应。

该文基于MATLAB程序编写Truss Spar平台在规则波情况下的运动响应分析程序，并且根据非线性动力学理论，在程序中考虑垂荡、横摇以及纵摇运动之间的耦合。其次，考虑系泊系统非线性力的影响以及瞬时波面升高的影响，研究Truss Spar平台的非线性运动特性。

1 运动方程的建立

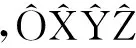
TrussSpar平台六自由度动态方程如下：

(1)

式中：[M]为平台质量矩阵；[ΔM]为平台附加质量矩阵；[C]为阻尼矩阵；[K]为静水恢复力矩阵；{F(t)}为波浪力向量；{Fm(t)}为系泊力向量；{X}为平台位移向量。

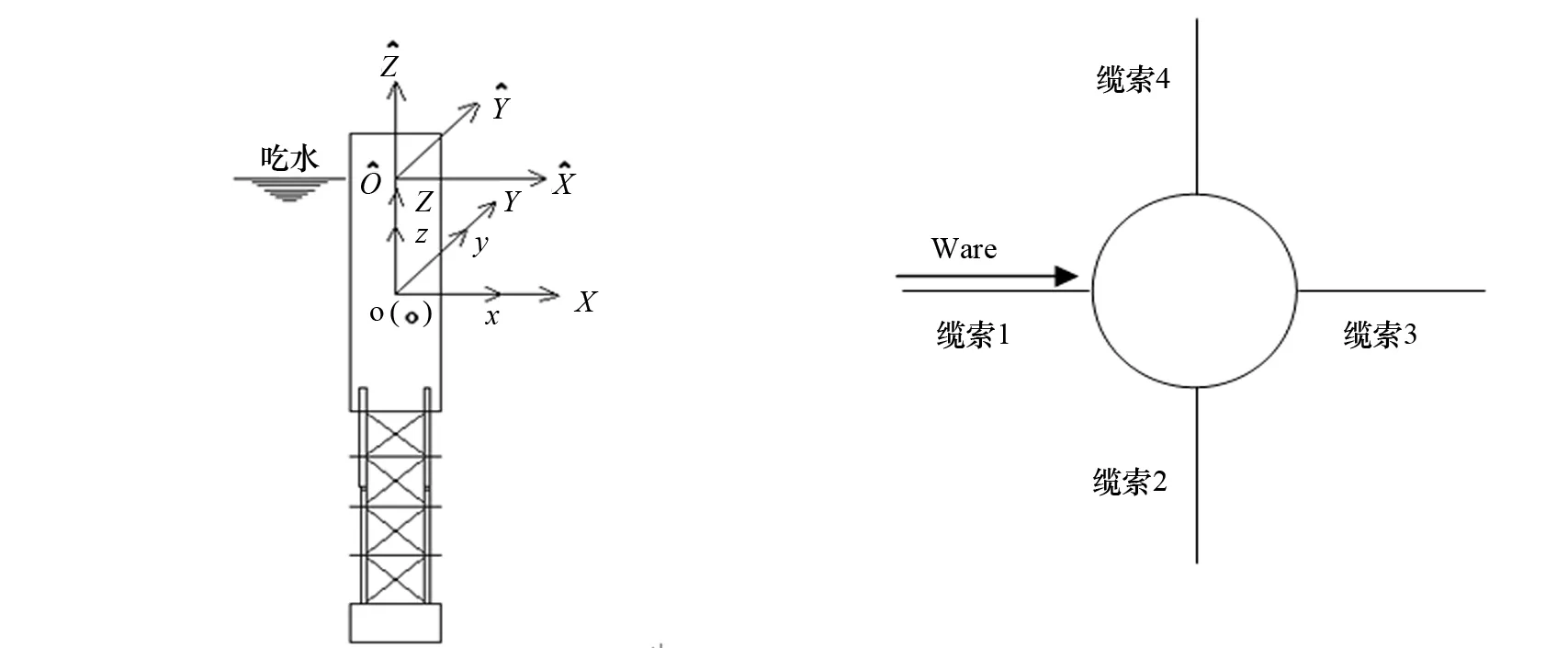
图1 平台坐标系 图2 四索系泊系统简图

TrussSpar平台的恢复力由两部分组成：静水恢复力和系泊恢复力。该文考虑垂荡、纵摇以及横摇三个自由度耦合运动，推导了静水中非线性垂荡恢复力、纵摇恢复力和横摇恢复力。对于系泊力的计算，采用弹性悬链线方程计算非线性系泊力。

2 恢复力

考虑平台在波浪中的垂荡、横摇与纵摇运动耦合，根据稳性原理推导出平台非线性垂荡恢复力、横摇恢复力矩以及纵摇恢复力矩如下[7]：

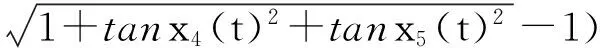
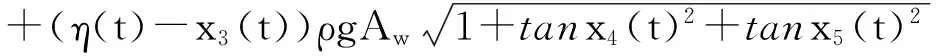
(2)

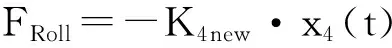
(3)

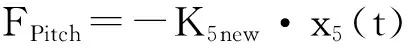
(4)

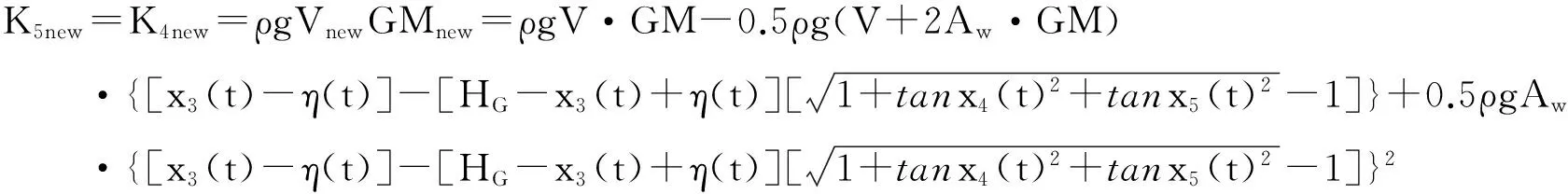
(5)

式中：FHeave为垂荡恢复力；FRoll为横摇恢复力矩；FPitch为纵摇恢复力矩；K5new、K4new分别为平台纵摇、横摇刚度； Aw为平台的水线面面积；ρ为海水密度；x3(t)为垂荡位移；x4(t)为横摇角；x5(t)为纵摇角；HG为静水面到重心的距离；η(t)为瞬时波面升高。

3 非线性系泊力

非线性系泊力采用弹性悬链线方程计算，弹性悬链线方程如式(5)和式(6)所示：

(5)

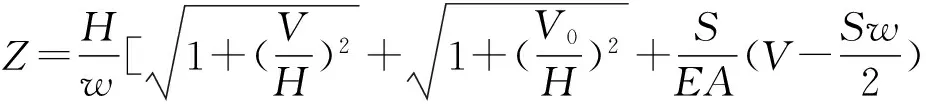
(6)

式中：X为锚泊线水平方向投影长度；Y为锚泊线竖直方向投影长度；H为上端点拉力水平分量；V为上端点拉力竖直分量；V0为锚泊线下端点拉力竖直分量；w为锚泊线线重度；EA为锚泊线轴向弹性模量；S为锚泊线未拉长时的长度。

该文选取分段式悬链线系泊缆，由三段缆索组成：上段缆索为船体链段，与平台主体连接；下段为海底链段，海底链段的末端与海底基础相连接；中间为重力压载链段，其比重却远大于首尾两段的钢缆，依靠自身重力，能够为平台本体提供更好的定位性能。系泊缆主要参数如表1所示。

表1 分段式悬链线系泊缆主要参数

根据弹性悬链线方程，绘制出单根分段式悬链线系泊缆的水平位移、垂直位移和相应的水平恢复力、垂直恢复力之间的关系曲线，如图3、图4所示。

由图3和图4可知，单根缆索的系泊力与位移的关系曲线具有非线性特性。缆索系泊力的水平分量与系缆点水平位移之间非线性关系表现得尤其明显，而系泊力的垂直分量，与水平力分量相比较，与位移之间的关系的非线性就要相对弱一些。关系曲线的斜率在缆索顶端点的位移值为零时，达到最大值，所以，缆索对平台本体运动的制约在这一时刻最明显。

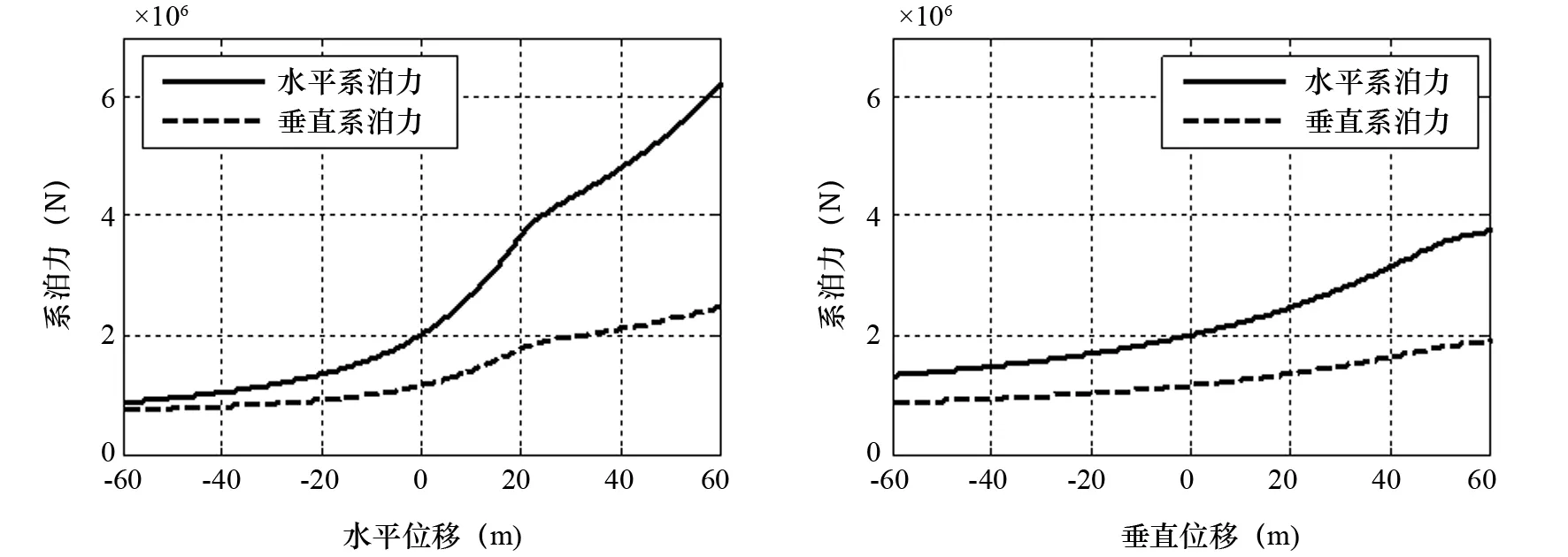
图3 单根缆索系泊力与水平位移关系曲线 图4 单根缆索系泊力与垂直位移关系曲线

4 计算分析

该文选用Truss Spar平台为研究对象，其主要参数见表2。从表2可知，平台垂荡与纵摇固有频率比满足2∶1内共振关系。为了验证使用龙格库塔方法求解的程序正确性，选取波浪周期25 s，浪向为0°，波幅WA为1 m，将无系泊、恢复力为线性情况下的计算结果与SESAM中Hydrod模块的计算结果相比较，如图5所示。从图5可以看出，数值模拟结果与SESAM结果基本一致，程序正确。

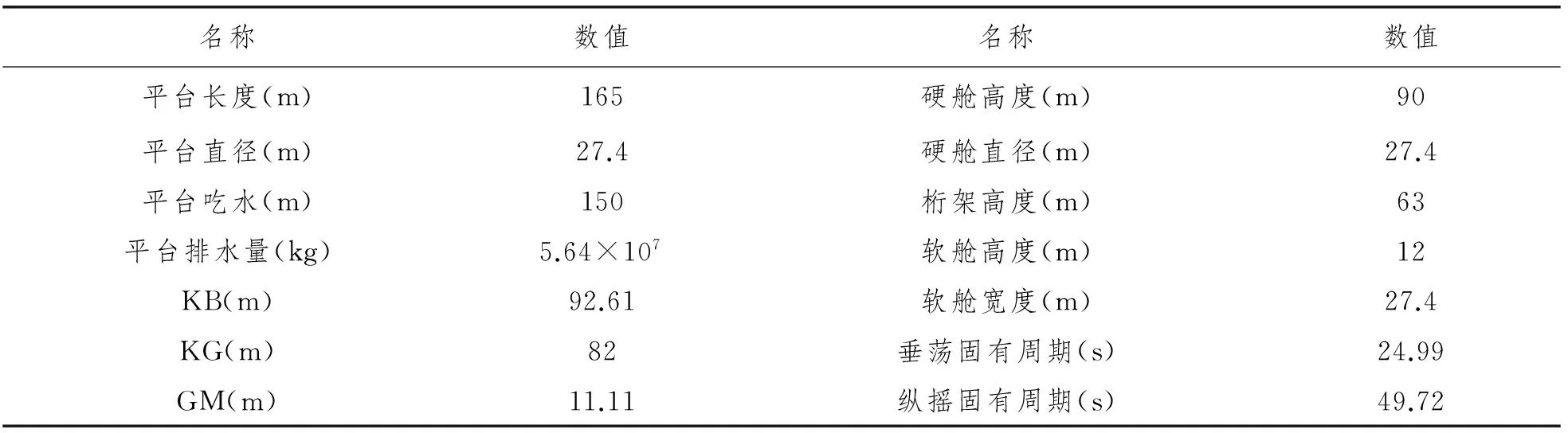
表2 Truss Spar平台主要参数

图5 Truss Spar 平台运动响应(T=25 s，WA=1 m)

研究考虑非线性系泊力时，选取波浪周期25 s，浪向为0°，计算 Truss Spar平台运动幅值随波高的变化，如图6所示。同时为了对比，将无系泊情况下恢复力为线性和非线性时的结果在图6中列出。

从图6可以看出，考虑非线性恢复力时，垂荡运动幅值大致不变，纵荡、纵摇幅值出现明显的跳跃现象,这表明平台垂荡模态能量将接近饱和。当波浪幅值进一步增大时，平台垂荡模态的能量会向纵荡、纵摇模态渗透，从而使纵荡、纵摇幅值迅速增大，且纵荡、纵摇幅值随波高非线性增加。与无系泊情况对比， Truss Spar平台在加系泊后，响应幅值发生跳跃的临界波高值增大，加系泊延缓了跳跃现象的发生，但是不能阻止内共振情况的发生,这一现象也被Rho在2003年所做的水池实验所验证[8]。同时从图6中可以看出，当平台的响应幅值发生跳跃之后，加系泊相对于无系泊情况下垂荡幅值增加，而纵荡、纵摇幅值减小。从而表明,施加系泊系统后,有效的减小平台的水平面运动。

为了获得在系泊情况下平台运动响应的详细情况，图7和图8给出了波浪周期等于25 s时不同波高情况下平台纵荡、垂荡以及纵摇位移的时间历程图。

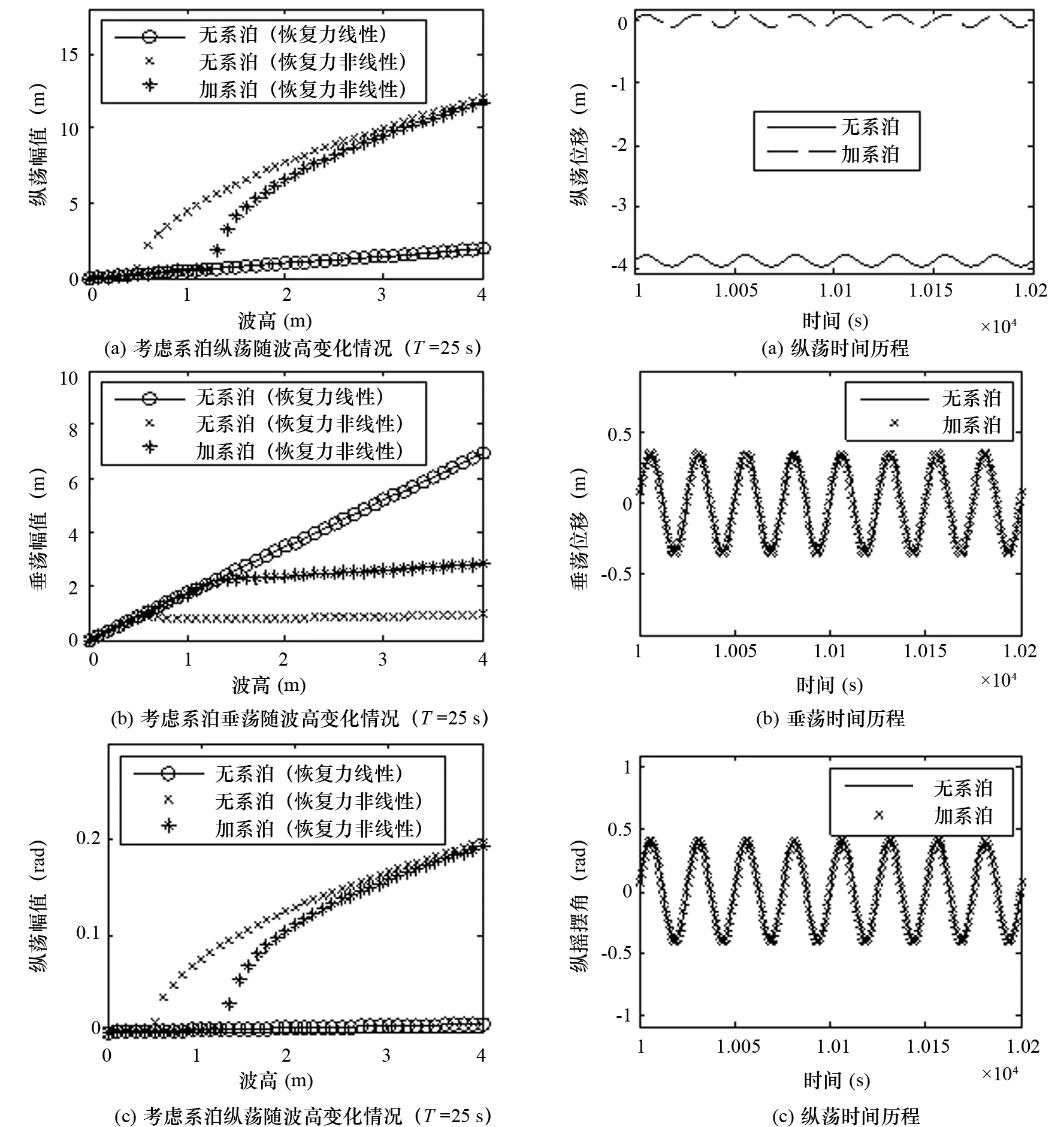
图6 平台纵荡、垂荡以及纵摇随波高变化情况 图7 考虑系泊平台纵荡、垂荡以及纵摇时间历程(Hwave=0.2 m)

从图7中可以看出，波高等于0.2 m时，波高较小，平台的纵荡、垂荡与纵摇以波浪频率为主做波频运动。由于考虑了系泊，平台的纵荡运动以初始时刻原点为中心做往复运动，而在无系泊情况下，平台以偏离原点-3.85 m为中心做往复运动。垂荡和纵摇运动在加系泊和无系泊两种情况下，运动形式基本一致。

从图8中可以看出，波高等于2 m，考虑系泊，垂荡运动以波浪频率做强迫振动，纵荡和纵摇以以波浪频率的1/2做亚谐运动。相对无系泊的情况，纵荡以原点为中心做往复运动，垂荡幅值增加，纵摇幅值减小。

为了研究波面升高对内共振现象的影响，选取周期25 s，浪向为0°的情况进行研究。平台运动纵荡、垂荡、纵摇幅值随波高变化如图9所示。

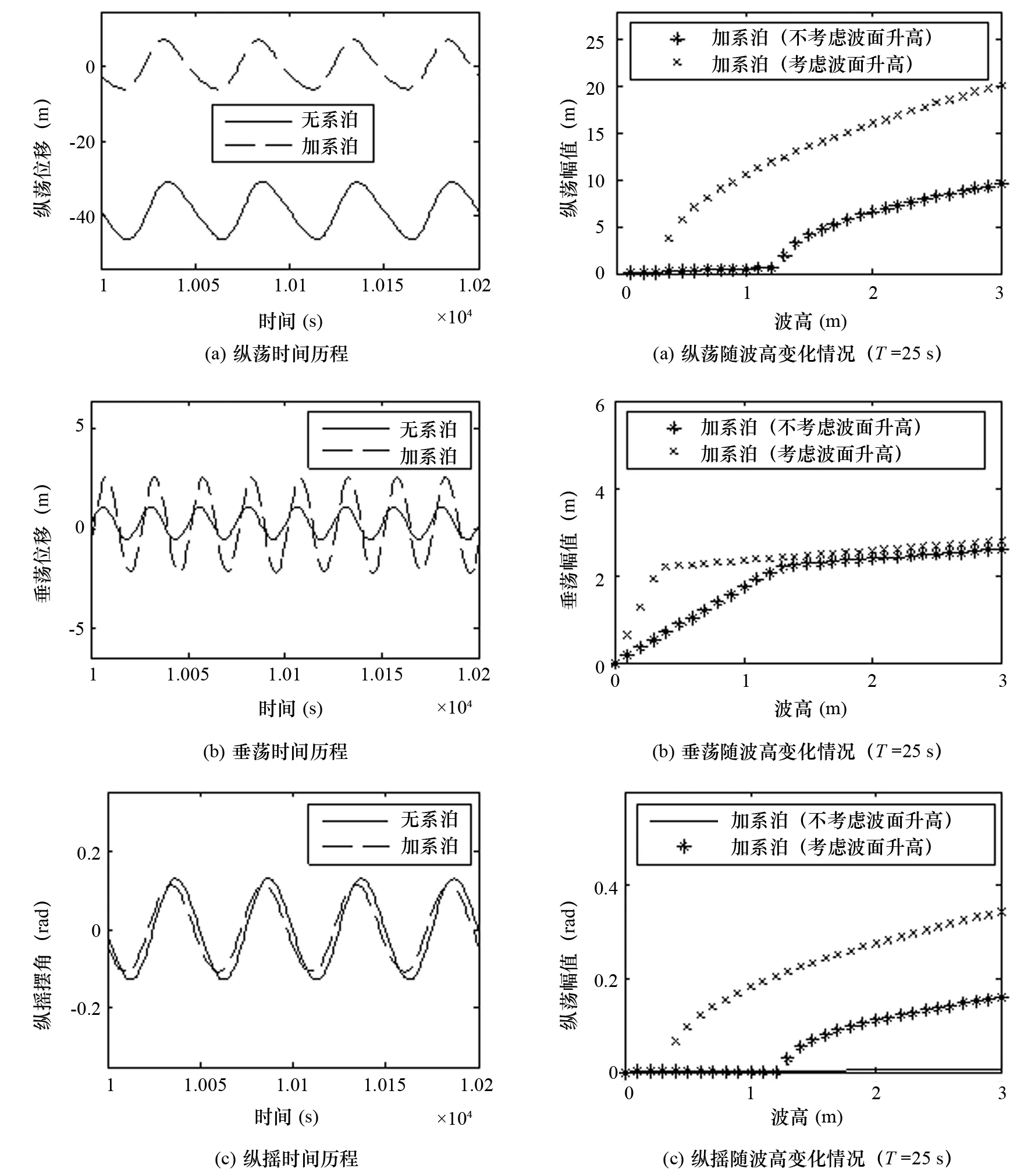
图8 考虑系泊平台纵荡、垂荡以及纵摇时间历程(Hwave=0.2 m) 图9 考虑波面升高平台纵荡、垂荡以及纵摇随波高变化情况

从图9中可以看出，在考虑波面升高之后，平台运动响应幅值发生跳跃时的临界波高值由1.3 m减少到0.4 m，平台越容易发生内共振现象。同时，在波幅较小时，考虑波面升高和不考虑波面升高，平台的纵荡及纵摇运动幅值差别很小，而垂荡幅值在考虑波面升高时随波高增加的斜率大于不考虑波面升高时的情况。当波高继续增加时，相对不考虑波面升高，纵荡、垂荡以及纵摇幅值都增加，且纵荡和纵摇幅值增加幅值较大。

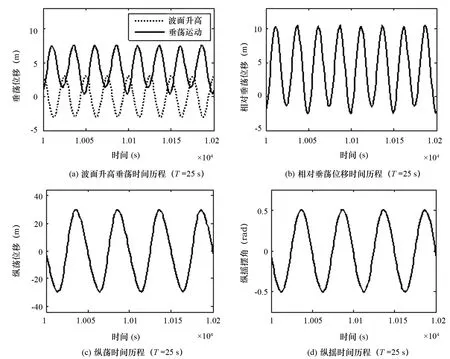
图10 考虑波面升高Truss Spar 平台运动响应(T=25 s，WA=3 m)

为了获得在系泊情况下平台发生内共振时运动响应的详细情况，图10给出了波浪周期等于25 s时不同波高情况下平台纵荡、垂荡以及纵摇位移的时间历程图。从图10可以看出，当波浪周期等于25 s时，平台垂荡运动整体偏离初始位置且向上移动，垂荡运动幅值出现非对称现象。这是由于垂荡恢复力中，存在着二次非线性项的影响，当考虑波面升高影响时，纵摇幅值大幅度增加，对垂荡运动恢复力产生了较大影响，从而对垂荡运动形式也产生较大的影响。同时，从图10(a)和图10(b)可以看出，当波面升高以较大幅值运动并且与垂荡运动有约90°相位差时，平台相对垂荡运动变化很大。平台相对垂荡运动的变化，将导致平台干舷剧烈的变化，这将对平台的安全产生影响。此外可以观察到，波浪周期等于25 s时，平台的垂荡运动以波浪频率做强迫运动，而纵荡与纵摇运动以波浪频率的1/2做亚谐运动。

5 结论

(1)考虑平台垂荡、横摇与纵摇之间的耦合，当波浪频率接近平台垂荡固有频率且波高较小时，纵荡、垂荡和纵摇幅值随波高线性增加，当波高超过某一临界值时，垂荡幅值大致保持不变，而纵荡和纵摇幅值曲线出现跳跃现象，表明平台垂荡模态能量将接近饱和；当波高进一步增大时，平台垂荡模态的能量会向纵荡、纵摇模态渗透，使纵荡、纵摇幅值非线性迅速增大，导致平台出现大幅纵荡和纵摇运动。

(2)考虑非线性系泊力之后，响应幅值发生跳跃的临界波高值减小，延缓了跳跃现象的发生，但是不能阻止内共振情况的发生。当平台的响应幅值发生跳跃之后，加系泊相对于无系泊情况下垂荡幅值增加，而纵荡、纵摇幅值减小，表明系泊系统的施加，有助于减小平台的纵荡与纵摇运动。

(3)当波浪频率接近平台垂荡固有频率时，在考虑波面升高之后，平台运动响应幅值发生跳跃时的临界波高值减小，平台越容易发生内共振现象。同时，考虑波面升高，当波面升高较大且与平台运动相位相差很大时，将引起相对垂荡运动的大幅增加。相对垂荡运动的大幅增加，将引起平台干舷的剧烈变化，对平台的安全将造成影响。

[1] Wang J，Berg S， Luo Y H, et al. Structural design of the truss spar-an overview[C]. Proceedings of the Eleventh International Offshore and Polar Engineering Conference. Stavanger, Norway, 2001.

[2] Downie M J，Graham J M R，Hall C, et al. An experimental investigation of motion control devices for truss spars[J]. Marine Structures, 2000, 13:75-90.

[3] Mekha B B，Johnson C P，Roesset J M. Nonlinear response of a Spar in deep water: different hydrodynamic and structural models[C], Proceedings of the Fifth International Offshore and Polar Engineering Conference. Netherlands, 1995.

[4] Ran Z，Kim M H.Coupled dynamic analysis of a moored Spar in random waves and currents (time-domain vs. frequency domain analysis[C], The 17th OMAE International Conference.Lisbon, 1999.

[5] MA W, Yao L M, ZOU J. Deepwater nonlinear coupled analysis tool[C]. The 2000 Offshore Technology Conference. Houston, 2000.

[6] Tahar A, Ran Z. Hull/mooring/riser coupled spar motion analysis with buoyancy-can effect[C]. Proceedings of the Twelfth International Offshore and Polar Engineering Conference. Kitakyushu, 2002.

[7] 唐友刚，沈国光，刘丽琴. 海洋工程结构动力学[M]. 哈尔滨：哈尔滨工程大学出版社，2008.

[8] Rho J B, Choi H S. An experimental study for mooring effects on the stability of spar platform[C]. Proceedings of the 13th International Offshore and Polar Engineering Conference. Honolulu, 2003.

CoupledDynamicAnalysisofaNonlinearlyMooredTrussSpar

ZHANG Liang1, LI Hong-xia2, WU Xiao-ni3

(1.ShangHai Merchant Ship Design & Research Institute, Shanghai 201203, China;2. School of Naval Architecture, Dalian University of Technology, Liaoning Dalian, 116024, China;3. The National University of Singapore, Singapore 118426, Singapore)

Truss Spar has been widely recognized as a viable option for the offshore industry to employ in deep and very deep waters. It is necessary to study the behavior of the truss spar. This paper focuses on the 6 degree of freedom heave-roll-pitch coupled motion performance of a truss spar. The nonlinear motion of Truss Spar with nonlinear mooring force was developed by Runge-Kutta method under the condition of internal resonance in which the ratio of heave natural frequency to pitch natural frequency is 2∶1. The influence of nonlinear mooring force on the motion of offshore platforms is studied with considering the effect of time-varying incident wave elevation. Numerical results show the critical wave height value of the jumping phenomenon in surge and pitch motion increases when the nonlinear mooring force was considered. The mooring force can delay the jumping phenomenon, but can not prevent the internal resonance. The increase in relative heave motion will result in the freeboard dramatic change and greatly influence the safety of Truss Spar when the wave elevation is considered.

Truss Spar ; nonlinear mooring force; wave elevation; coupled motion; internal resonance

2014-01-23

张 良(1987-)，男，助理工程师。

1001-4500(2015)01-0019-08

P75

：A