基于LTE系统的一种低复杂度的球型译码算法*
袁冬冬,仇润鹤(1.东华大学信息科学与技术学院,上海201620;2.数字化纺织服装技术教育部工程研究中心,上海201620)
基于LTE系统的一种低复杂度的球型译码算法*
袁冬冬1,2,仇润鹤1,2
(1.东华大学信息科学与技术学院,上海201620;2.数字化纺织服装技术教育部工程研究中心,上海201620)
针对球型译码检测算法在信道条件较差时检测复杂度大的问题,在分析比较传统的检测算法的基础上,提出了一种降低球型译码复杂度的算法。该算法采用固定阈值作为可靠性判断标准,将迫零检测算法与球型译码算法相结合,首先利用迫零检测算法对传输数据进行检测,然后对迫零算法检测出来的数据进行可靠性判断,若检测出来的数据可靠性高则采用迫零算法作为最终结果,若可靠性较低则对数据进行球型译码,同时利用迫零检测结果来选择球型译码算法的初始半径。通过仿真得出,在4x4天线下该算法在保证误码率基本不变的情况下大大降低了球型译码的复杂度。关键词:LTE系统迫零检测 球型译码检测 可靠性判断
0 引 言
移动通信长期演进LTE(Long Term Evolution)采用MIMO和OFDM技术,具有频谱利用率高,信道容量大,频谱分配灵活等特点,必将在未来的移动通信中发挥巨大的作用。虽然LTE通信系统带来了更大的数据传输速度,但是速率的增加给信号的检测技术提出了更大的挑战,尤其是在采用VBLAST(基于贝尔实验室的垂直空时分层编码)时,在发送端每根天线都携带不同的信息,正确的检测出发送信号更加困难。为了保证LTE系统具有较高的性能,LTE的检测算法的选择至关重要。传统的LTE检测算法主要有最大似然算法ML(Maximum Likelihood)、迫零检测算法ZF(Zero Forcing)、最小均方误差算法MMSE(Minimum Mean Square Error)、球型译码算法SD(Sphere Decoder)c等。在文献[1-2]中对这几种算法进行了讨论,仿真证明ML为最优算法但ML算法的缺点是复杂度呈指数增长无法实用化;ZF检测算法具有最低的复杂度,但是误码率较高;MMSE算法也有较高的误码率;球形译码算法是一种性能接近于ML算法但复杂度低的检测算法,它的基本思想是以接收矢量Y为球心,预先设定一个搜索半径C,通过对球内点的循环搜索不断减小搜索半径,最终找到最具可能性的发送向量。与ML检测算法相比,由于限制和缩小了搜索范围,需要搜索的点数也大量减少,从而复杂度显著降低了,因此球型译码算法是近些年研究的热点。但是尽管球型译码算法具有比ML算法复杂度低的特点,但是相对于MMSE和ZF算法仍有很高复杂度,如何进一步的降低球型译码的复杂度是近些年人们研究的焦点。目前对球型译码算法的研究主要集中在初始半径的选择和搜索路径的优化这两个方面。在半径选择上,文献[3]给出了一种快速算法,降低初始半径对检测算法复杂度的影响,在误码率和系统复杂度上取得了均衡;文献[4]给出了一种降低信道噪声影响的半径选择方法,根据信噪比不同选择不同的初始半径,减小了信道噪声对初始半径选择的影响;文献[5]对低信噪比环境下的半径进行抑制,使低信噪比环境下的复杂度减小;在搜索路径优化方面,文献[6]使用采用了一种低复杂度的候选列表生成算法,降低了球型译码的复杂度。文献[7]提出了一种基于路径度量减少搜索路径的策略,通过与路径度量阈值的比较来进行搜索路径的修剪,有效降低了复杂度;尽管这些改进算法降低了球型译码复杂度,但检测复杂度相对于线性检测算法依然很高,为了进一步降低球型译码算法复杂度,本文提出一种降低球型译码算法复杂度的新算法,该算法首先利用ZF检测算法对传输数据进行检测,然后对检测出来的数据进行可靠性判断,若检测出来的数据可靠性高于设定阈值,则采用ZF算法作为最终结果;若可靠性低于设定阈值,则对数据进行球型译码,同时利用ZF检测结果来选择球型译码算法的初始半径。因为ZF算法的复杂度远远的小于SD球型译码,因此该新型算法在保持较低误码率的同时,大大降低了球型译码的复杂度。
1 一种低复杂度的球型译码算法
1.1 LTE系统接收端模型
LTE系统中采用的是MIMO和OFDM相结合的信号处理技术,在发射端进行串并转换、层映射、预编码等,生成OFDM基带信号,在接收端就是对其求逆的过程,简化的信号接收端的结构如图1所示。
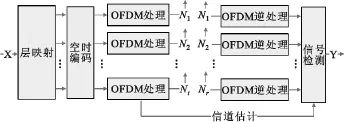
图1 LTE系统中接收端模型Fig.1 Receiving-terminalmodel of LTE system
在LTE系统中,发送端的复值信号被映射到Nt个发射天线端口,生成OFDM基带信号后在各个天线端口下发射出去。发射信号经过无线信道到达至Nr个接收天线,各个接收天线同时接收所发送的数据,并进行OFDM基带信号处理,利用信号检测算法判决检测出发送端发送的信号。
如果不存在符号间的干扰,则MIMO系统的输入输出的关系为

式中,H是大小为Nt×Nr的矩阵,其中H(i,j)元素表示第i根发射天线到第j根接收天线间的增益系数; N为加性高斯白噪声,其均值为0,方差为滓2。X为发送信号矩阵,Y为接收信号矩阵。
1.2 一种新型的球型算法ZF-SD译码检测算法
球型译码算法在搜索半径C确定后并非每次搜索过程都有满足条件的坐标点存在,为了降低球形译码算法的复杂度同时保证在每次搜索过程中都有满足条件的半径内的点,本文提出了ZF-SD算法,该算法通过可靠性判断来将ZF算法和SD算法相结合,同时利用ZF检测产生的估计值来作为初始半径的选择依据,来进一步降低复杂度。
ZF-SD算法首先在接收端进行ZF检测,获得ZF检测的估计值,然后对进行可靠性判断,其可靠性为:
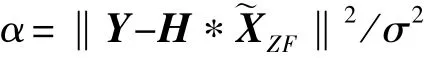
其中,Y为接收到的信号,軒XZF为待判定的信号为噪声的方差,椰·椰为Frobenius范数。
本文采用固定阈值的方法来作为可靠性判断的标准,经过实验仿真,最终确定琢的阈值选取为二倍的接收天线数。当琢小于接收天线数的二倍时,即琢≤2Nr就认为检测数据可靠。也即椰Y-H*椰2≤2*Nr*滓2,其中Nr为接收天线的个数。
由于在ZF-SD检测过程中,首先得到了ZF检测的估计值軒XZF,所以对于可靠性不能满足判断准则的估计值要进行球型(SD)译码检测。为了保证每次搜索过程中约束半径内都能搜索成功,ZF-SD算法令初始搜索C=椰Y-H*椰,根据该式可以看出,不管C取值多大,总会存在一个点F包含在以C为半径的球域之内。从而保证在每次搜索过程中至少有一个点满足条件,避免了扩大半径重新搜索的情况。
则对于球型检测部分,搜索范围约束条件为:
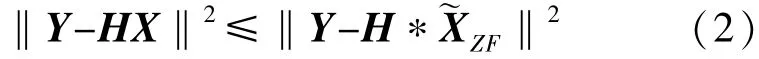
对信道矩阵H进行QR分解,得到H=QR,其中Q是酉矩阵,QHQ=I。对于发送天线Nt和接受天线Nr相等时,R为上三角矩阵。
由于正交矩阵相乘不改变范数,所以式(2)可写为:

接收机在整个发射信号空间中搜索满足式(3)的信号矢量,令y′=QHY,并选择和接收信号最接近(欧氏距离最小)的矢量作为发射信号的估计值:
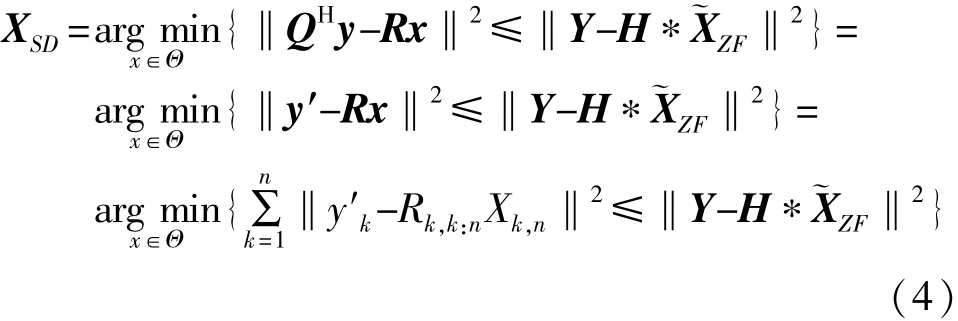
式(4)中,Rk,k:n表示矩阵R的第k行的第k列到第n列的元素组成的行向量,Xk,n表示向量X的第k个元素到第n个元素组成的向量,向量X中的每个元素Xi取自一个实数。集合Θ表示为星座图中所有可能点的集合。对式(4)进一步的分解可以表示为:

由式(6)可以看出在检测第n层时,只有xn这一个待估计值,因此从第n层开始检测。

由式(9)可以看出,球型检测部分的搜索方式是一个迭代关系,其复杂度依赖于球型检测半径Ck的收敛速度。xn为球型检测搜索的根节点,每一个可能的xn点存在都将产生一个树形搜索的树形结构。
1.3 ZF-SD检测算法流程
ZF-SD检测算法的流程可以概括为以下几个步骤:
4)输出最终结果X。
ZF-SD算法流程可以用图2表示。
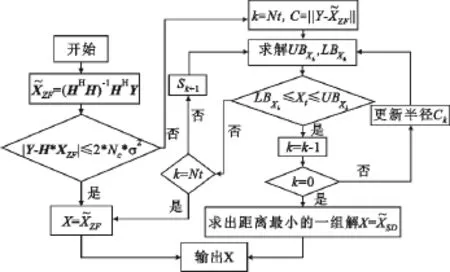
图2 ZF-SD算法的检测流程Fig.2 Detecting processes of ZF-SD algorithm
由图2可知,本文提出的ZF-SD检测算法充分利用了ZF检测复杂度低和SD检测算法误码率性能高的优点,复杂度的大小取决与可靠性的判断。如果有更多的检测结果軒XZF被判定为可靠,则其算法复杂度则接近ZF检测算法;若有更多的軒XZF被判定为不可靠,则其算法复杂度接近SD算法。因此通过阈值的设定可以调节ZF-SD算法的复杂度和误码率性能。
2 仿真结果与分析
本文对ZF-SD检测算法的误码率进行了仿真,采用蒙特卡洛方法随机的发送10 000个数据,调制方式采用QPSK,发送和接收天线为4×4,图3为采用ZF-SD算法误码率曲线,其中可靠性判断为琢≤8,也即琢≤2Nr。
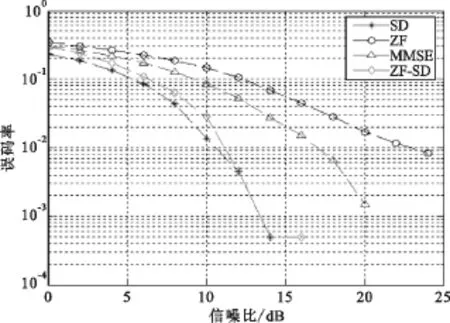
图3 琢≤8时ZF-SD检测算法的误码率曲线Fig.3 BER curves of ZF-SD when琢≤8
由图3中所得的误码率曲线图可以看出,ZFSD算法的误码率曲线接近球型译码算法,尤其是在信噪比大于10 dB时,ZF-SD算法与SD球型译码算法基本一样。而ZF算法和MMSE算法在误码率性能上与ZF-SD算法还有较大差距。
为了找到误码率和复杂度上最优的选择,本文同时对不同可靠性阈值判别方法进行了仿真,仿真条件相同,为4×4天线,采用蒙特卡洛方法,产生10 000个发送数据,调制方式为QPSK。仿真结果如图4所示。
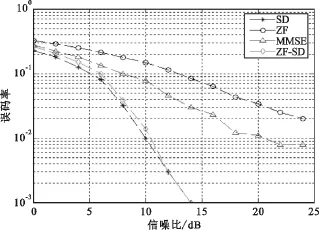
图4 琢≤6时ZF-SD检测算法的误码率曲线Fig.4 BER curves of ZF-SD when琢≤6
由图4中的误码率曲线可以看出,当琢≤6,ZFSD算法误码率性能依然很接近SD球型译码检测算法,但相对与琢≤8时ZF-SD算法的误码率性能更加接近SD球型译码算法,这是由于可靠性阈值的变小会有更多的点采用SD球型译码检测算法。
为了能够得出ZF-SD算法的复杂度,本文对ZF-SD检测算法的复杂度进行了仿真。为了获取更加准确的复杂度,本次仿真采用了10 000个数据,调制方式采用QPSK,发送和接收采用4×4天线,在MATLAB下的仿真曲线如图5所示。
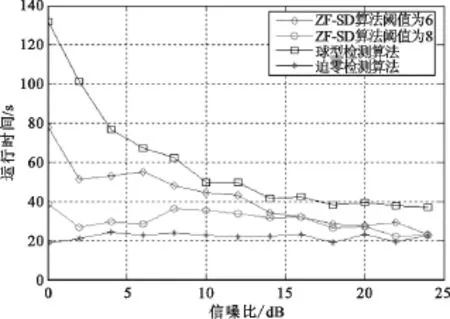
图5 不同阈值下的ZF-SD算法复杂度Fig.5 ZF-SD algorithm complexity under different thresholds
在图5中,横坐标表示信噪比,纵坐标表示系统运行的时间。由仿真图可以看出随着信噪比的增加,检测算法的运行时间逐渐降低。在信噪比小于5 dB时,ZF-SD算法的运行时间远远的小于SD球型译码算法。在信噪比为5 dB时,阈值为8的ZFSD算法运行时间大约30 s,阈值为6时ZF-SD算法运行时间大约55 s,而SD算法的运行时间为75 s, ZF-SD算法在复杂度方面优于SD算法;在信噪比大于10dB时,检测算法的运行时间趋于平衡,ZFSD算法的运行时间大约是SD算法的70%。ZF检测算法的运行时间最低且信噪比的增加对ZF检测的运算时间没有影响,这是因为ZF算法运算中没有考虑噪声影响,因此信噪比的增强并不会对ZF算法的复杂度造成影响。
同时,从图5也可以看出采用阈值为8的ZFSD算法在信噪比小于10 dB时运行时间远小于采用阈值为6的ZF_SD算法。由于采用阈值为8和阈值为6的ZF-SD算法在误码率性能方面基本相同,因此采用阈值为8的ZF-SD算法在实际运用中更加可行,也即椰Y-H*軒X椰2/滓2≤2Nr作为可靠性的判别更加可行。
3 结 语
在现代通信中,降低系统的误码率和算法的复杂度一直是工程应用中追求的目标。本文在SD球型译码检测算法的基础上提出了ZF-SD算法,该算法集合了SD算法误码率低和ZF算法复杂度低的优点,将两种算法相结合,在保持误码率性能不变的情况下,大大降低了系统的复杂度,通过仿真,说明该算法在误码率和复杂度上取得了较好的折中,在实际的LTE通信系统中具有一定的实用价值。
[1] Chang D-C,Guo D-L.Spatial-division multiplexing MIMO detection based on a modified layered OSIC scheme[J].IEEE Transactions on Wireless Communications.2013;12(9):4258-71.
[2] Cai S,Duan Z,Gao J,editors.Comparison of different virtual MIMO detection schemes for 3GPP LTE[C].5th International Conference on Wireless Communications, Networking and Mobile Computing,WiCOM 2009,Beijing,China:IEEE Computer Society,September 24, 2009-September 26,2009:1-5.
[3] 陈云杰,吴耀军,居贝思.基于MIMO系统的球形译码算法的改进[J].通信技术,2010,43(06):24-25,28. CHEN Yun-jie,WU Yao-Jun,JU Bei-si,Improved Sphere Decoding for MIMO System[J],Communications Technology,2010(06):24-5+8.
[4] 陈发堂,侯彦庄.基于MIMO-OFDM系统的一种低复杂度球型译码检测算法[J].计算机应用研究, 2011(09):3436-3438. CHEN Fa-tang,HOU Yan-zhuang.Low Complexity Sphere Decoding Detection Algorithm based on MIMOOFDM System[J],Application Research of Computers, 2011,09:3436-3438.
[5] 李世平,苗承强,刘立京.一种低复杂度MIMO球形检测算法[J].计算机工程,2013(02):81-84,89. LI Shi-ping,MIAO Cheng-qiang,LIU Li-jing.A Sphere Detection Algorithm with Low Complexity for MIMO[J],Computer Engineering,2013,02:81-84+89.
[6] Nguyen HD,Ahmad U,LiM,editors.A computationally efficient soft-output Lattice reduction-aided selective spanning sphere decoder for wireless MIMO systems[C]. 2013 IEEE 24th Annual International Symposium on Personal,Indoor,and Mobile Radio Communications,PIMRC 2013,London,UK:Institute of Electrical and Electronics Engineers Inc September 8-11,2013;786-790. [7] Wang S,Guo X,Sun S,etc.A tree pruning algorithm for MIMO sphere decoding based on path metric[C]. IEEE 75th Vehicular Technology Conference,Yokohama, Japan:Institute of Electrical and Electronics Engineers Inc,May 6,2012-June 9,2012:1-5.
YUAN Dong-dong(1989-),male,graduate student,mainly engaged in wireless communications and remotemonitoring;
仇润鹤(1961—),男,博士生导师,教授,主要研究方向为通信与信息系统、宽带无线通信与应用。
Qiu Run-he(1961-),male,doctoral tutor,professor, mainly engaged in communication and information systems, broadband wireless communications and applications.
A Low-Com plexity Algorithm of Sphere Decoding in LTE System
YUAN Dong-dong1,2,QIU Run-he1,2
(1.College of Information Sciences and Technology,Donghua University,Shanghai201620,China;2.Engineering Research Center of Digitized Textile&Fashion Technology,Ministry of Education,Donghua University,Shanghai201620,China)
Aiming at the high complexity of SD(Sphere Decoding)detection algorithm under poor channel conditions and based on the analysis and comparison of traditional detection algorithms,this paper proposes amethod for reducing the complexity of SD algorithm.This algorithm adopts a fixed threshold as the reliability criterion and combines ZF(Zero Forcing)algorithm with SD algorithm.Firstly ZF algorithm is used to detect the transmitted data,and then determine the reliability of ZF data.And if the data enjoys high reliability ZF algorithm would be adopted as the final result;if the data is less reliable,SD algorithm be used. Meanwhile,ZF detection result is used to select the initial radius of SF algorithm.Simulation shows that this algorithm could greatly reduce the complexity of SD algorithm whilemaintaining the error rate almost unchanged in 4×4 antenna.
LTE;ZF algorithm;SD algorithm;reliability judgment
date:2014-09-14;Revised date:2014-12-26
TN929.5
A
1002-0802(2015)02-0151-05

袁冬冬(1989—),男,硕士研究生,主要研究方向为无线通信与远程监控;
10.3969/j.issn.1002-0802.2015.02.007
2014-09-14;
2014-12-26

