风险调整收益的最新研究进展及分类
陈磊+梁僖
摘 要:风险调整收益是评价投资组合绩效的重要指标,过去数十年涌现了大量的相关文献。对这些相关文献进行整理综述,并按照风险测度方法的不同将指标分为基于方差、β系数、偏矩、价格跌幅、VaR的风险调整收益指标五类。投资者可以根据其风险偏好选择最适合的评价指标。
关键词:夏普比率;业绩评估;风险调整收益
投资者最关心的莫过于投资组合的业绩表现,评价投资组合或单项资产的绩效有助于分析资产投资特性,及时调整投资策略。风险调整收益是一类重要的业绩评价方法,其基本思路是对收益加以风险调整得到一个综合性指标,以体现风险对收益的影响。本文将对20世纪60年代至今出现的重要风险调整收益指标做一个分类综述。
一、基于方差或贝塔系数的传统风险调整收益指标
1966年诺贝尔经济学奖得主威廉·夏普[1]基于资本市场线理论提出夏普比率,计算公式为:
SR=(1)
式中rP表示考察期间组合平均收益率,rF为无风险收益率,σP为以收益率标准差表示的总风险。夏普比率是目前应用最广泛的绩效评价指标,其值越大说明投资绩效越好。
夏普比率是一个相对比率,有些偏好绝对收益的投资者需要一个能更加直观地衡量业绩的指标,M2测度[2]因此对夏普比率做出改写:
M2=rP+SR×(σM-σP) (2)
或
M2=(rP-rF)×+rF (3)
其中σM表示市场组合或基准组合风险。M2测度与夏普比率对组合业绩的排序是一致的。
与夏普比率类似的有特雷诺比率(Treynor Ratio)[3],其分母用贝塔系数βP计算的系统风险替代了标准差:
TR= (4)
特雷诺比率忽略了非系统风险,而国内很多投资基金的资产组合都没有完全分散化,并不适宜用特雷诺比率评估绩效。
詹森指数(Jensen—α)[4]和特雷诺比率同样以证券市场线为基础,但它是一个绝对指标:
α=rP-E(rP)=rP-[rF+(rM-rF)βP] (5)
rM为评价期间市场组合平均收益率,α>0说明组合绩效优于市场绩效。
Treynor和Black[5](1973)提出的估价比率(Appraisal Ratio)中用到了詹森指数:
Appraisal Ratio= (6)
其中σε是非系统风险的度量。若组合已经充分分散化,则非系统风险很小,估价比率应该很大,故在某种程度上估价比率也可以说是对组合分散程度的一个评估。
基金经理的投资风格和目标各不相同,在评估绩效时应有一个基准做比较,信息比率[6](Information Ratio)应运而生:
IR= (7)
dP是实际业绩与基准业绩间差异收益率的均值,σdP是差异收益率的标准差,通称跟踪误差(Tracking Error),反映了积极管理的风险。信息比率越大说明积极管理的绩效越好。
统计研究表明,大部分权益类金融产品回报率的概率分布都呈现尖峰厚尾的特征,夏普比率的正态性假设将低估组合风险。Pézier[7](2006)提出经偏度和峰度调整的夏普比率,负偏态分布和高峰度将使得调整后的值较调整前有所下降:
Adjusted Sharpe Ratio=SR×1+×SR-×SR2 (8)
二、基于半方差的风险调整收益指标
后现代资产组合理论(Post-modern Portfolio Theory,PMPT)认为,按照投资风险的定义,应只将收益率相对均值的负向波动计入风险,由此衍生出一系列风险调整绩效指标。
下行风险[8](Downside Risk)只反映资产价格降低的风险:
σD= (9)
这里rT表示可接受的最低目标收益率,可以选取无风险收益率、基准组合收益率或其他固定的阈值,ri为投资组合各期收益率。
预期损失可能[8](Downside Potential)定义为:
Downside Potential= (10)
Downside Potential实际上就是一阶下偏矩(Lower Partial Moments,LPM),σD是二阶下偏矩的开方。对应地还有Upside Potential[9]:
Upside Potential= (11)
Shadwick和Keating[10]在2002年提出了一个收益损失比——OmegaRatio:
Ω== (12)
Ω值越高,绩效越好。也可修改成与夏普比率相近的形式:
Omega-SharpeRatio=(13)
由于Omega-SharpeRatio=Ω-1,两者的绩效排序是完全相同的[11]。
Sharpe Ratio和Omega-SharpeRatio的一个自然延伸是由Sortino[12](1991)提出的Sortino Ratio:
Sharpe Ratio=(14)
三、基于VaR方法的风险调整收益指标
VaR[13](Value at Risk)风险价值,指在一定的置信水平下,某一金融资产或证券组合在未来特定一段时间内的最大可能损失,是目前国际流行的风险测度指标。使用VaR作为风险测度的夏普式比率被称为收益风险价值比率[14](Reward to VaR):endprint
Reward to VaR=(15)
这里的VaR ratio表示VaR使用百分比而非数量的形式。VaR依然不能保证损失不超过给出的数值,如果需要考虑超出置信水平外的损失,应使用条件VaR[15](Conditional VaR)。将Reward to VaR中的分母改为条件VaR就是条件夏普比率[16]:
Conditional Sharpe Ratio=(16)
就偏度和峰度对VaR做出调整得到修正VaR(Modified VaR)[17]。将夏普比率的分母改成MVaR则得到修正夏普比率[18]:
Modified Sharpe Ratio= (17)
四、基于收益跌幅的风险调整收益指标
收益跌幅(Drawdown)指投资期内一次无间断的资产缩水幅度,其均值即平均跌幅(Average drawdown):
D=(18)
这里Dj指考察期(通常为三年)内第j个收益跌幅,d为下跌总数。有人认为,只有收益率序列中最大的几次下跌才能说明问题,因此也可以限定d为常数,比如3或5。
历史最大跌幅(Maximum drawdown)指某特定时间段(通常取三年)内投资者可能遭受的最大损失,即在最高点买入在最低点卖出的损失,一定程度上反映了组合管理者风险控制的能力。
基于收益跌幅有三种广泛使用的风险估值指标,分别是Calmar比率、Sterling比率和Burke比率,常用于评价管理期货基金和对冲基金。
Calmar比率是1991年Terry Young[19]提出的:
Calmar Ratio=(19)
表示历史最大跌幅,经典的Calmar比率使用最近三年的月度数据计算。Calmar比率越高,基金业绩越好。
Sterling比率的最初提出者很可能是Deane Sterling Jones[20],后来改成类似夏普比率的形式:
Sterling Ratio=(20)
Sterling比率使用三年的年度数据计算,因此在敏感度上不如Calmar比率。实际上,最常用的Sterling变式是Sterling比率和Calmar比率的结合,分母使用三年年平均最大跌幅[21]:
Sterling-Calmar Ratio= (21)
Burke[22](1994)提议通过平方和开根号的方式,突出剧烈下跌相对于温和减值的影响:
Burke Ratio= (22)
1987年Peter Martin[23]提出溃疡指数(Ulcer Index,也称Martin Index):
Ulcer Index= (23)
D'i表示第i期收益率相比历史最高水平的跌幅,n为使用数据的期数,Martin建议使用周度或者每日数据。溃疡指数考虑了下跌的持续时间,有助于识别那些仅在短期有收益或者长期来看实际没有收益的资产。Martin比率(Martin Ratio or Ulcer Performance Index,UPI)使用溃疡指数作为分母:
Martin Ratio=(24)
应避免投资溃疡指数高的资产,除非其经风险调整后仍然表现出超高的收益率。
五、总结
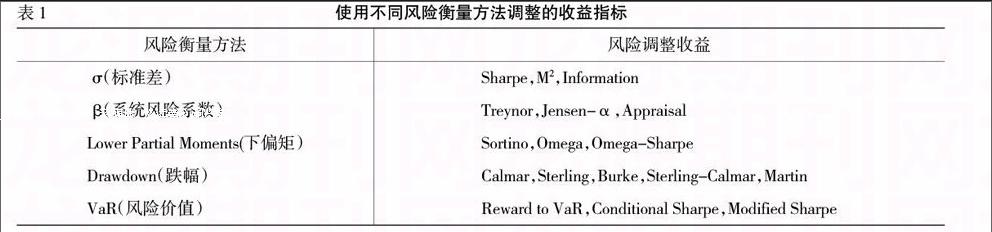
综上所述,过去数十年来,风险调整业绩指标研究发展迅速,按照风险测度方法的不同,分类总结(见表1)。
我们该如何从中选择一个最优的绩效评价指标?Eling和Schuhmacher[24]的研究表明这些指标形式相近且高度相关,绩效排序结果大致相同,许多其他文献也印证了他们的观点。然而不同指标反映了不同的风险偏好,例如VaR和跌幅类指标比较注重风险,适于保守型的投资者,而那些乐观的投资者会更偏向于偏矩类指标。因此,投资者可以选取最能反映自己风险偏好的指标来评价资产组合绩效,帮助做出投资决策。
参考文献:
[1] SharpeWilliam F.MutualFundPerformance[J].Journalof Business,1966,(1):119-138.
[2] Modigliani Franco,Modigliani Leah.Risk-Adjusted Performance[J].Journal of Portfolio Management,1997,(2):45-54.
[3] TreynorJ.L.HowtoRateManagementofInvestmentFunds[J].HarvardBusinessReview,1965,(1):63-75.
[4] JensenMichael C.The Performance of Mutual Funds in the Period 1945-1964[J].Journalof Finance,1968,(2):389-419.
[5] TreynorJ.L.,Black Fischer.How to Use Security Analysis to Improve Portfolio Selection[J].Journalof Business,1973,(1):66-86.
[6] Goodwin T.H.The Information Ratio[J].FinancialAnalysts Journal,1998,(54):34-43.endprint
[7] Pézier J.,White A.The Relative Merits of Investable Hedge Fund Indices and Funds of Hedge Funds in Optimal Passive Portfolios[A].
ICMA Centre Discussion Papers in Finance DP2006-10[C].2006.
[8] Harlow W.V.,Rao R.K.S.Asset Pricing in a Generalized Mean—Lower Partial Moment Framework:Theoryand Evidence[J].Journal of Financial
and Quantitative Analysis,1989,(3):285-309.
[9] Edwin H.N.,Michael N.R.,Jun Y.Distinguishing Upside Potential from Downside Risk[J].Management Research News,2009,(1):26-36.
[10] Shadwick W.F.,Keating W.F.A Universal Performance Measure[J].Journal of Performance Measurement,2002,(3):59-84.
[11] Bacon Carl R.PracticalPortfolioPerformanceMeasurementandAttribution[M].Second Edition.Hoboken,New York:John Wiley & Sons,2008.
[12] Sortino F.,van der Meer R.Downside Risk[J].Journal of Portfolio Management,1991,(4):27-31.
[13] Morgan J.P.Risk Metrics—Technical Document[Z].4th Ed.New York:Morgan Guaranty Trust Company,1996:1-66.
[14] DowdK.Adjusting for Risk:An Improved Sharpe Ratio[J].International Review of Economics and Finance,2000,(3):209-222.
[15] RockafellarR.T.,UryasevS.Optimization of Conditional Value-at-risk[J].Journal of Risk,2000,(3):21-41.(下转213页)
(上接149页)
[16] Agarwal V.,Naik N.Y.Risk and Portfolio Decisions Involving Hedge Funds[J].Review of Financial Studies,2004,(1):63-98.
[17] FavreL,José-AntonioG.Mean-modifiedValueatRiskOptimizationwith Hedge Funds[J].Alternative Investments,2002,(5):21-25.
[18] Gregoriou G.N.,Gueyie J.P.Risk-adjusted Performance of Funds of Hedge Funds Using a Modified Sharpe Ratio[J].Journal of Wealth
Management,2003,(6):77-83.
[19] Young Terry W.Calmar Ratio:A Smoother Tool[J].Futures,1991,(1):40.
[20] McCafferty T.The Market Is Always Right[M].New York:McGraw-Hill,2002.
[21] Bacon Carl R.PracticalPortfolioPerformanceMeasurementandAttribution[M].Second Edition.Hoboken,New York:John Wiley & Sons,
2008:89-90.
[22] Burke G.A Sharper Sharpe Ratio[J].Futures,1994,(3):56.
[23] Martin P.G.,McCann B.R.The Investors Guide to Fidelity Funds[M].New York:John Wiley & Sons,1989.
[24] Eling M.,Schuhmacher F.Does the Choice of Performance Measure Influence the Evaluation of Hedge Funds?[J].Journal of Banking
and Finance,2007,(9):2632-2647.endprint

