巧妙“变”化在数学中的应用
广东省韶关市浈江区曲仁中学 蔺 勇
数学不同于其它学科,“灵活多变”是数学的最大特点,而变化最主要体现在变解法和变题目,这两方面运用得当,对于老师的教学和学生的学习都有积极的促进作用,能达到举一反三的效果。结合教学实践,本文从这两方面入手,谈谈巧妙变化在数学中的应用。
一、巧变题目解法
常规教学乃至高考,都特别强调“通法通解”,不可否认,这种方法是应用基础知识的体现,比较实用,相对容易理解。然而,“通法通解”有其自身的局限性,尤其像高考这种大型考试,有些题目用此方法难以解决,就算能解决,也会耗费大量的时间,运算量之大超乎想象。如何找到捷径,能省时省力,这就需要老师们在平时的教学中注重变化。巧妙的变化可使问题迎刃而解,达到事半功倍的效果,而这种方法的使用,必须注重对公式的变形应用。
例1、(2011年山东高考题)已知动直线l与椭圆C:交于P(x1,y1)Q(x2,y2)两不同点,且ΔOPQ的面积其中O为坐标原点。
(Ⅰ)证明:均为定值;(Ⅱ)设线段PQ的中点为M,求的最大值;(Ⅲ)椭圆C上是否存在三点D,E,G,使得?若存在,判断ΔDEG的形状;若不存在,请说明理由。
该题结构简洁、通俗易懂、形式优美、内涵深刻,是一道十分优美的高考解几题。其标准答案给出的解法是通法,但运算量极其大,而且没有体现出该题的“内在美”,相反的让人望而生畏。下面来看该题的一种优美解法:
解:(Ⅰ)因为P(x1,y1)Q(x2,y2),所以
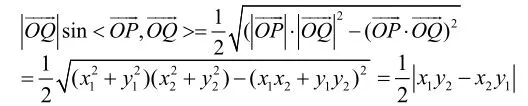
又所以
又由柯西不等式得
所以
当且仅当 时,等号成立。
因为点P(x1,y1)Q(x2,y2)在椭圆C:上,所以从而由均值不等式得
当且仅当时,等号成立。
由①、②得即不等式②的等号成立,于是由不等式②的等号成立的条件得,故均为定值。
(Ⅱ)由(Ⅰ)知所以
所以,所以,当且仅当时,等号成立。故的最大值为。
(Ⅲ)假设椭圆C上是否存在三点,使得成立,则由(Ⅰ)知:所以又为不同的三点,所以在x3,x4,x5中,只能有两个相等另一个为其相反数,不妨设 x3=x4,x5=-x4,则由椭圆的对称性知D,O,G或E,O,G三点共线,这与矛盾。故椭圆C上不存在满足条件的三点D,E,G。
上述优美解法的获得正是从三角形面积公式的变形开始,途中既没有联立方程组的繁琐运算,又避免了分类讨论。特别是这种解法不仅揭示了该题的本质结构特征及其“内在美”,而且也充分体现了用代数手段去研究几何图形性质的方法的多样性,令人拍手称绝。
变形是简解、巧解、妙解、美解的助推器,是培养学生创新意识与能力的重要载体。一个适当的变形,就可生长出巧解、妙解,省时省力,何乐而不为呢!
二、巧变题目(变式训练)
变式训练对培养学生发散思维有极大的帮助,是学生创新思维的必备前提,也是一种良好的学习品质。变式训练重点在于对某个问题进行多层次、多角度、多方位的探索,恰当与否的变式训练,在教学中起着至关重要的作用。
变式训练中应该体现以下特征:
1、设计变式训练首先应该能够体现数学的层递性
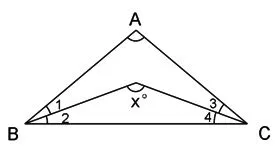
例1、如图∠1=∠2,∠3=∠4,∠A=100°求X的度数。
变式:已知三角形ABC的∠B和∠C的平分线B E、C M相交于点M。求证:(1)∠B M C=1 8 0°-(∠ABC+∠ACB)
(2)∠BMC=90°+ ∠A
改变为变式训练的题目,改变∠BAC的度数,求∠BMC和∠BAC的关系。
对已知题目进行了大胆的组合和拓广,由易到难,由数字到字母。其已知条件和结论体现数学有数向代数的转变,而这恰恰是学生应掌握的重点和难点。此题不仅锻炼了学生用类比的方法去思考和学习,而且促进学生对解决问题的思路理解得更为透彻。每问每一变都体现层层递进,步步深入,环环相扣的密切联系。
2、变式训练设计应能够体现知识的规律性和关联性,便于学生思考问题时思路的发展
例2、求函数的单调区间和值域。
分析:(1)关于形如的单调性与函数u=f(x)(f(x)〉0)复合函数的单调性,当a〉1时相同,当0〈a〈1时相反,即同增异减。
(2)关于复合函数单调性的研究,既是高考的热点,又是学生的弱点,因而是我们学习的重点。处理这类问题应把握好以下三点:①抓住中间变量的变化状态;②掌握复合函数的单调性规律;③注意复合函数的定义域。
3、变式训练应该能够体现命题的前瞻性,尽量贴近高考
例3、(2012辽宁理)已知等差数列{an}满足a2=0,a6+a8=-10。
(Ⅰ)求数列{an}的通项公式;(Ⅱ)求数列的前n项和。
解析:(Ⅰ)an=2-n,解法从略;
(Ⅱ)设数列的前n项和为Sn。由(Ⅰ)知,an=2-n,所以
令,则整理,得即,比较两边的系数,得,解得A=-2,B=0,从而所以
一般结论:若{an}是公差为d(d≠0)的等差数列,{bn}是公比为q(q≠1)的等比数列,则数列的前n项的和:
变式训练:已知求数列{an}的前n项的和Sn。
解析:令则整理,得,比较两边的系数,得
解 得从 而所 以
通过对这个题目的解答,可以让学生充分体会灵活多变,尝试通过题目,总结题目和思路,真正学会解决问题。所以在平时的教学中设计一题多变应贴近高考题型,及早着手培养学生有良好的思考习惯和思维品质。
变中有不变,变中求同,相信通过巧妙变化的教学设计,既能促进学生的提高,更能促进教师的提高。

