一种应急疏散最短路径的数学建模方法
禤家裕
(清远市人防(民防)指挥信息保障中心)
一种应急疏散最短路径的数学建模方法
禤家裕
(清远市人防(民防)指挥信息保障中心)
针对城市应急疏散的路径选择,运用数学方法讨论了最短路径的建模问题。使用模糊概念和图论分析方法分别对应急疏散路径规划优化中的路径权值量化和结点约束图转化进行分析,给出相应的解决方法,并结合简单例子说明了解决问题的步骤与方法。
应急疏散;模糊概念;权值量化;最短路径;数学建模
0 引言
城市在发生重大灾害性事件时,必将面临市区人员疏散问题。目前,对人员应急疏散规划的研究,理论上主要包括数学分析和仿真2种方法。国外有学者提出用最大流方法进行路径选择,目的是在路网同行能力许可的范围内,最大饱和度地从最优路径将疏散者从危险区域疏散至安全区域;亦有运用最小代价流问题进行疏散路径分配(即最短路撤退规划,SEP方法),目的是将全部人员疏散至指定区域路径总行程的最小化;影响较大的是Cova等提出的基于车道的网络流模型[1],它针对复杂网络计算应急疏散的最优路径,模型将研究对象抽象为一个最小费用流的优化问题。本文从数学分析建模的角度介绍一种应急疏散路径优化的方法。
1 路径权值量化
道路网络中路径权值的量化是进行路径优化分析的前提。一般情况下,可将道路长度作为路径权值。在实际疏散过程中影响路径权值的因素很多,如疏散路面状况、疏散人群结构状况、疏散易发生事故状况、疏散指挥人员配备及设施指示情况等。因此,应将诸多因素加以考虑而得到一个更客观的路径权值。但各因素间存在很大的不确定性与模糊性,难以找到统一的定量计算公式。而模糊概念则为处理客观事物中,存在概念外延不确定的情况提供了一种解决方法。
1.1 路径量化分析
由以上分析可知,影响路径权值的因素除长度可


1.2 路径量化算法
根据模糊数学原理,构建模糊综合评价函数需要3个要素[2]:
1) 因素集,定义为

将式(4)代入式(3),得到非理想情况下的路径权值。
若对某道路因素集的每个因素对照评价集进行评价,路面状况 “很好”、“较好”、“一般”、“较差”、“很差”的比例分别为25%、30%、30%、10%、5%。单因素评价矩阵中因素1的评判结果

2 结点约束转化及最短路径算法
理想化的应急疏散最短路径与实际最短疏散路径一般情况下是不相同的。因为实际的疏散线路必须遵循一定的疏散规则,如某路口不能左转,某道路不能逆行等。理论上,这类问题都可以归结为结点有约束的最短路径求解问题,通过特定的步骤将其转化为无约束最短路径求解问题,是进行数学建模的关键[3]。一般的解决步骤为:
1) 根据路径网给出的拓扑关系建立结点间的连通关系表,如表1所示,表的第一列为前序结点,第一行为后续结点,结点间直接相连的结点用“√”表示,其余的不填;
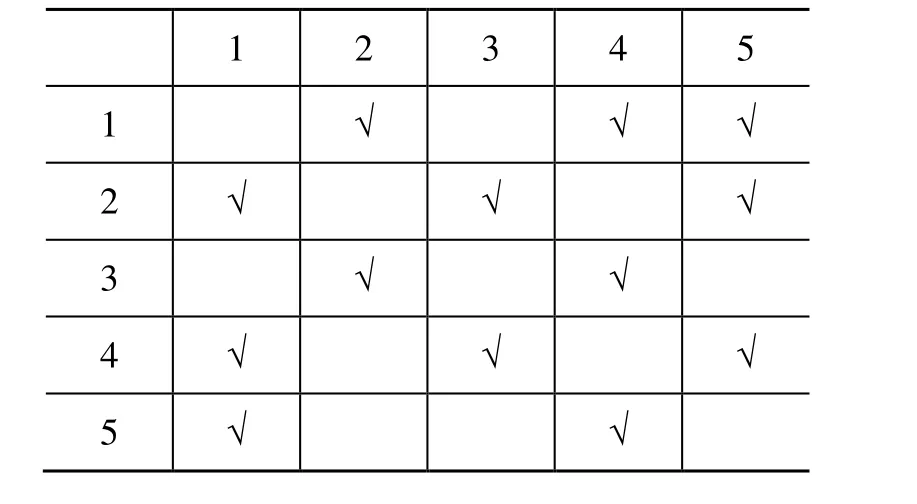
表1 结点连通关系表
2) 根据路径网络给出的限制条件,得到约束结点及对应的点对,如图1中约束结点及对应点对可以表示为{4,(5,1)};
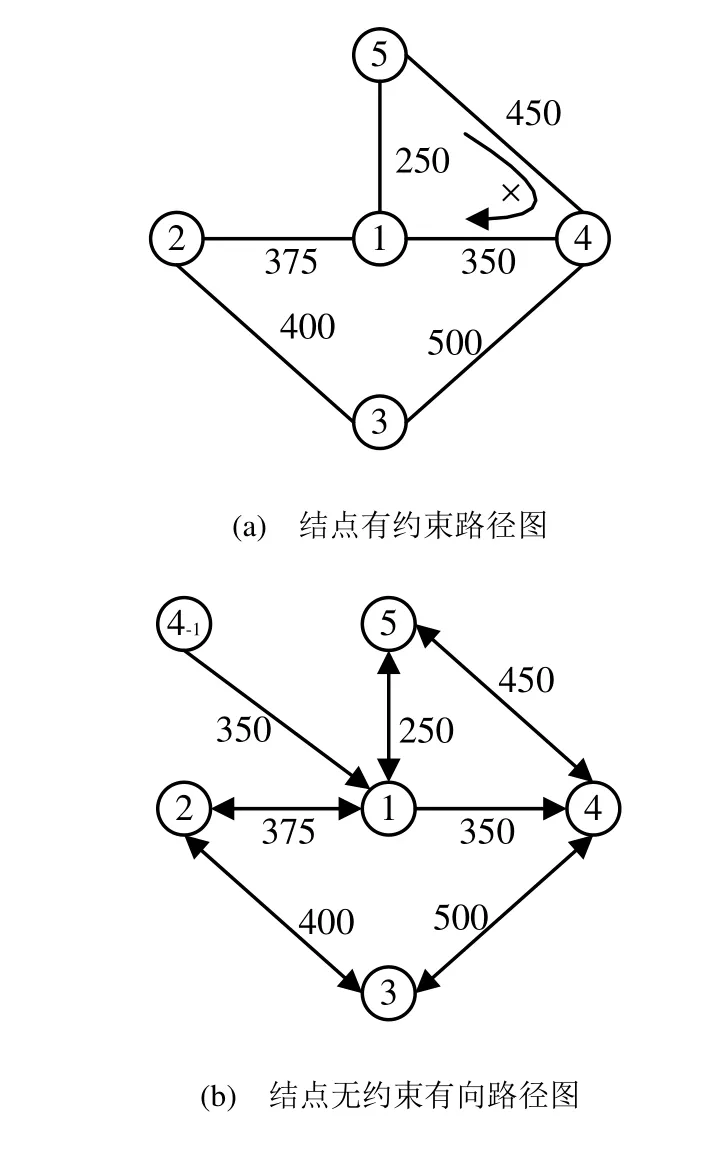
图1 结点有约束路径图与结点无约束有向路径图的转化

路径权值量化后道路网络拓扑如图1(a)所示[4],据此建立如表1所示的结点连通关系表。根据步骤3)的方法,可将结点有约束的最短路径求解问题图1(a)转化为结点无约束的有向图最短路径求解问题图1(b),而后者的求解通常可以用Dijkstra及Floyd算法解决。
3 结语
本文对应急疏散最短路径规划中路径权值量化和结点约束转化的问题进行分析并给出了相应的解决办法,对城市应急管理部门具有一定的参考价值。但是,人员疏散的实际情况往往比较复杂,要对目标区域环境进行各方面的综合评价与建模才能作出更优化的疏散路径算法。
[1] Cove T J, Johnson J P. A network flow model for lane-based evacuation routing[J].Transportation Research Part A, 2003,37(1):579-604.
[2] 陈玉敏,龚健雅.基于模糊数学的多因素道路网权值确定算法[J].武汉大学学报:信息科学版,2007,32(10):928-931.
[3] 王锐.城市防空人口疏散问题研究[D].郑州:解放军信息工程大学,2004.
[4] Fred Buckley, Marty Lewinter.图论简明教程[M].李慧霸,王凤芹,译.北京:清华大学出版社,2008.
A Mathematical Modeling Method of the Shortest Emergency Evacuation Route
Xuan Jiayu
(Civil Air Defense Command Information Security Center of Qingyuan City)
For the choice of the city emergency evacuation route, we discussed the modeling problem of the shortest path by using mathematical method. We analyzed the weight quantization of emergency evacuation path planning optimization and constrainted-node graph transformation by using fuzzy concept and graph analysis method respectively, gave the corresponding solutions and showed the steps of solving problems in combination with some simple examples. Finally we illustrated actual use value and deficiency of the method.
Emergency Evacuation; Fuzzy Concept; Weight Quantization; Shortest Path; Mathematical Modeling
禤家裕,男,1983年生,工学硕士,工程师,主要从事人防指挥信息化的研究与应用。E-mail: 179241391@qq.com

