基于PID神经网络的四旋翼飞行器控制算法研究
胡锦添舒怀林
(1.广州市光机电技术研究院 2.广州大学机械与电气工程学院)
基于PID神经网络的四旋翼飞行器控制算法研究
胡锦添1舒怀林2
(1.广州市光机电技术研究院 2.广州大学机械与电气工程学院)
针对四旋翼飞行器的姿态与位置控制问题,提出基于PID神经网络的控制方法。建立四旋翼飞行器的数学模型,引入四旋翼飞行器联合仿真平台,利用Matlab设计PID神经网络姿态控制器,训练后能达到良好的控制效果,最后设计PID神经网络位置控制器并进行训练。仿真结果表明,该控制方法在性能上明显优于传统PID,对飞行器有良好的控制效果。
四旋翼飞行器;PID神经网络;姿态控制
0 引言
微型飞行器概念从20世纪90年代提出后,迅速引起了世界各国的关注。同常规飞机相比,微型飞行器具有体积小、隐蔽性好、质量轻、成本低、灵活性强、携带方便、操作简单等突出特点,因此无论在军事领域还是民用领域,微型飞行器都有十分诱人的应用前景[1]。一些工业先进国家已投入大量人力和财力研制各种微型飞行器。
微型四旋翼飞行器是由4个旋翼驱动的无人机,其结构简单、灵活性强、负载能力大,并可实现垂直起降、空中悬停等动作。它有6个自由度,通过4个旋翼的转动提供升力,只要分别改变4个旋翼的转速,即可改变飞行器的飞行姿态[2]。四旋翼飞行器是一个强耦合、非线性、多变量的欠驱动系统,为了增强飞行器的稳定性与安全性,必须建立准确的数学模型和设计智能型控制系统,这是当今飞行器研究的重点与难点[3]。
随着MEMS技术与计算机技术的不断发展,四旋翼飞行器的控制策略研究也取得了相应的进展,国内外研究人员分别提出了PD控制、PID控制、反步法、滑模控制等控制方法[1-4]。这些方法基本能控制飞行器的飞行姿态,但仍然存在不足:PD控制稳定性不强,在模型参数摄动时控制效果不理想;PID控制、反步法以及滑模控制均对模型进行了线性化处理,忽略了模型的非线性部分,精度不高,影响控制效果。要取得良好的控制效果,必须建立准确的飞行器数学模型以及使用现代控制技术设计控制器。本文利用PID神经网络技术设计四旋翼飞行器控制器,并在联合仿真平台上进行仿真,结果显示PID神经网络能很好地对四旋翼飞行器多变量系统进行解耦控制,获得良好的飞行控制效果。
1 数学模型的建立
四旋翼飞行器的结构图如图1所示。
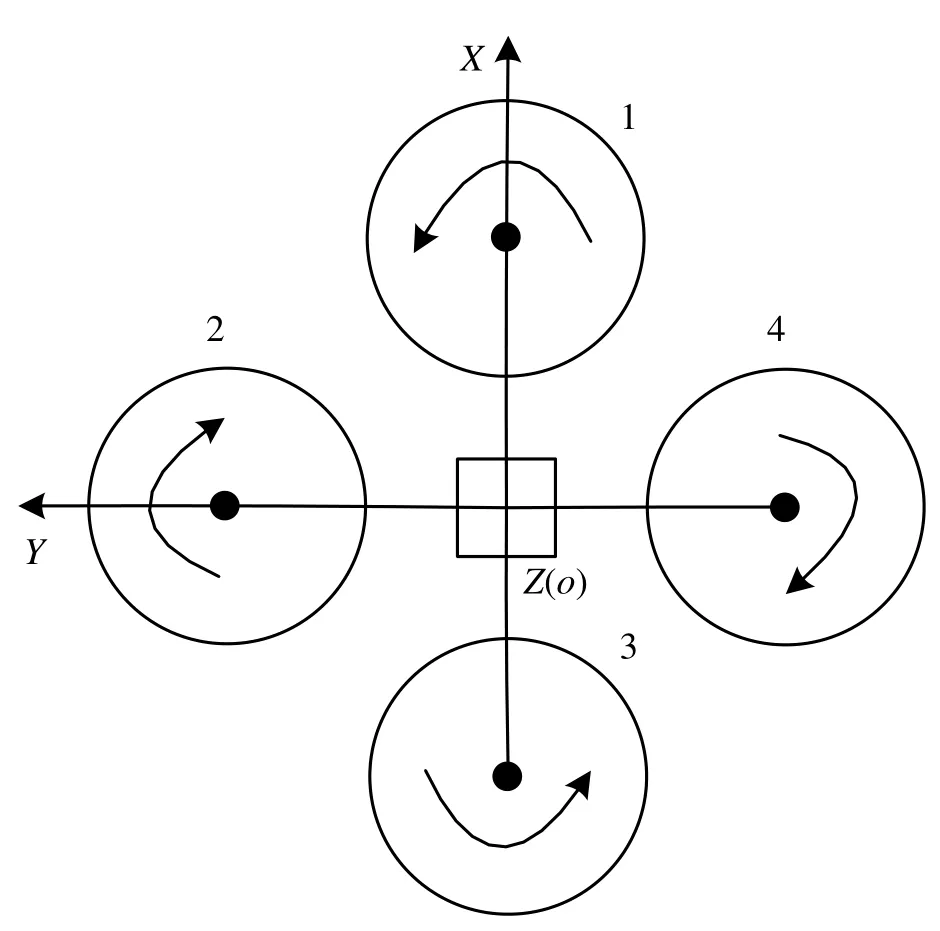
图1 四旋翼飞行器结构图
分析飞行器的飞行原理,根据牛顿-欧拉方程和坐标转换矩阵建立飞行器的动力学模型[5],如式(1)所示。

其中,m为飞行器质量;g为重力加速度;μx、μy、μz分别为X轴、Y轴、Z轴3个方向上的空气阻力系数;Jx、Jy、Jz分别为飞行器绕X轴、Y轴、Z轴的转动惯量;Jr为电机外转子与螺旋桨的转动惯量;λ为各个旋翼的反扭矩产生偏航力矩的比例系数。


2 PID神经网络
PID神经元网络是一种由比例(P)、积分(I)和微分(D)神经元组成的多层神经网络,同时具备经典PID控制和神经网络控制的优点。对于多变量强耦合时变系统,PID神经网络先通过在线学习、设置初始值;再根据对象参数发生变化对系统输出性能的影响自动调整连接权值;最后通过改变网络中比例、积分和微分作用的强弱,如同经典PID控制器的参数整定,使系统具备较好的动态性能,达到对系统进行解耦控制的目的[6],其结构如图2所示。
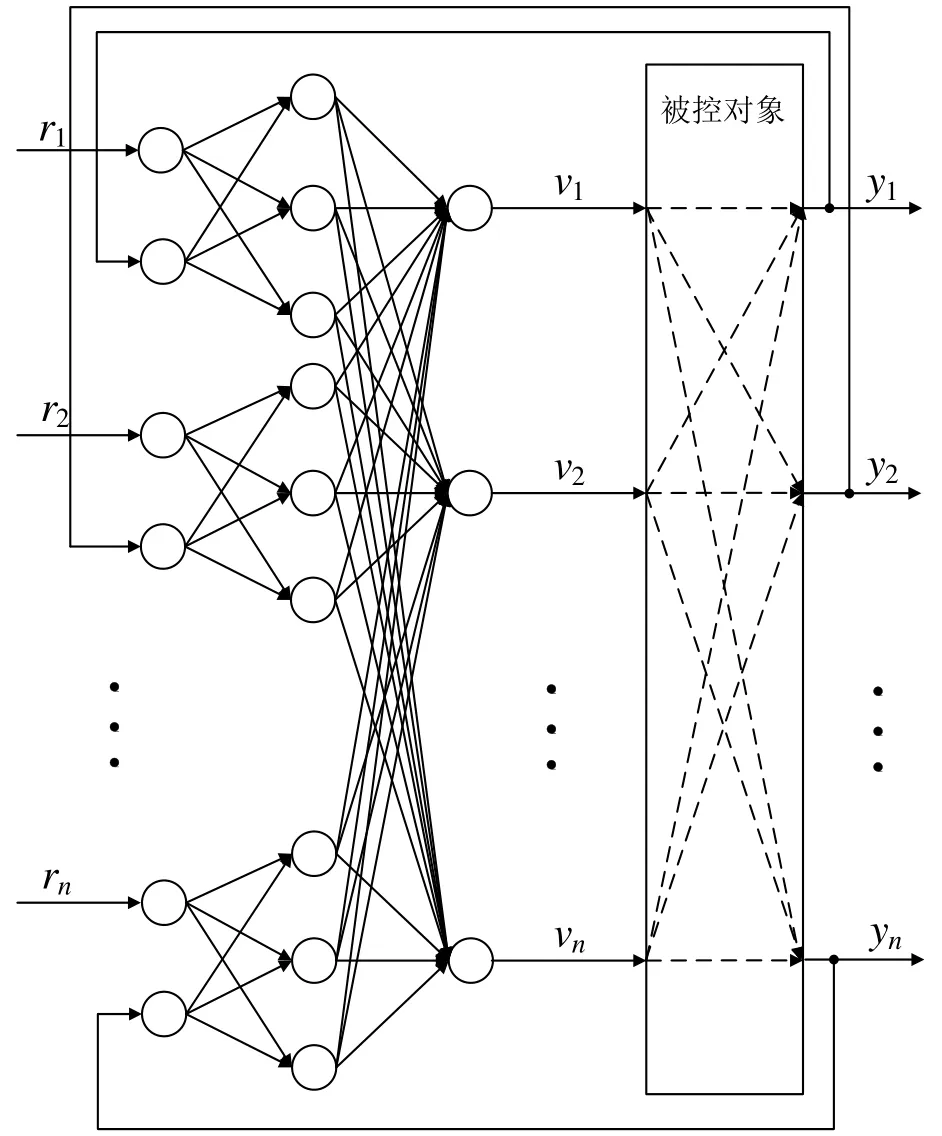
图2 PID神经网络多变量控制系统结构
PID神经网络是一种新的多层前向网络,它除了具有一般多层前向网络的特点,如逼近能力、并行计算、非线性变换特性外,其隐层单元还分别具有比例(P)、积分(I)和微分(D)等动态特性,适合多变量系统的控制与辨识[7]。利用PID神经网络技术设计四旋翼飞行器的控制器,对四旋翼飞行器进行解耦控制,使其具有快速稳定的飞行控制效果。
3 PID神经网络姿态控制器的设计
由前述的四旋翼飞行器动力学模型可知,对于多输入多输出的非线性控制系统,通常在建模过程中无法建立精确模型,必须对模型进行线性化处理,忽略其非线性部分,使模型精度降低。因此,本文利用动力学建模分析软件Adams建立四旋翼飞行器的结构模型,再导出其非线性动力学模型,模型输入变量为4个旋翼的升力,输出变量为3个欧拉角,最后导入Matlab/Simulink中建立飞行器的联合仿真平台[8]。
利用 Simulink中的工具模块建立飞行器姿态控制系统的模型,并根据PID神经网络算法,利用S函数模块创建PID神经网络控制器,如图3所示。

图3 四旋翼飞行器姿态控制系统
建立控制系统后,设置仿真参数,初始化PIDNN的各个变量,先通过经典PID控制器整定适用的PID参数,再将其设定为隐含层到输出层的连接权初值[9],然后输入参数(Pitch_r, Roll_r, Yaw_r)=(1,1,1),其仿真结果如图4所示。

图4 初始化后PIDNN系统的输出
从图 4可知,选取适当的连接权初值,PIDNN系统的输出等价于传统 PID控制系统的输出,所以PIDNN控制器的初值选择可以根据经验PID数值决定或者根据传统PID控制器的参数整定方法选取。
初始化系统后,对PIDNN进行训练,训练324步后系统的输出,如图5所示。
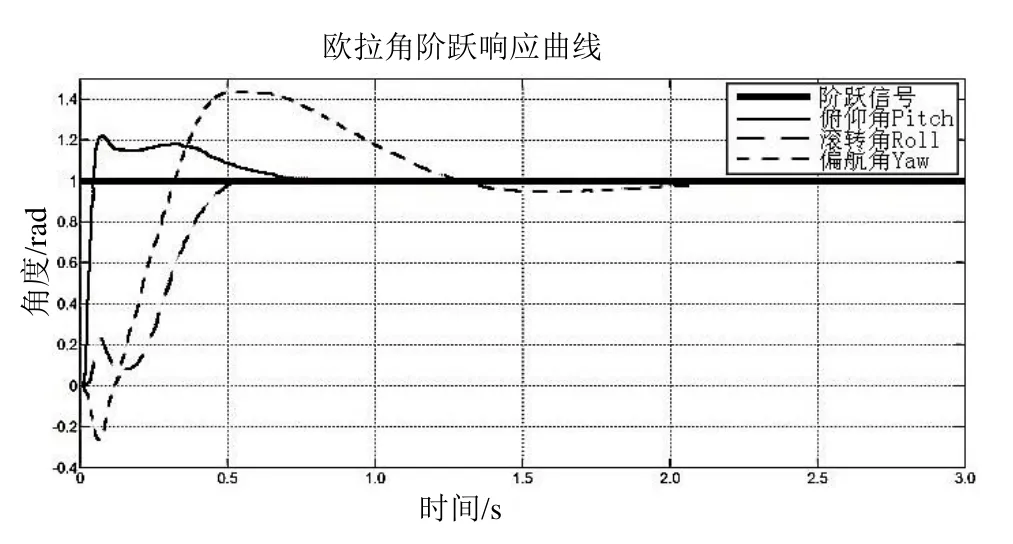
图5 训练324步后系统的输出
从图5可以得出,经过训练后的PIDNN控制器,实现对3输入3输出的强耦合,非线性飞行器系统广义的结构控制。系统3个被控量分别按各自的输入给定值变化,受到其他给定值的影响较小,系统的响应速度更高,超调更小,无静态误差。其中,滚转角Roll基本无超调且能在t=0.6 s达到稳定;俯仰角Pitch超调量变小,角度输出误差为+10 deg,在t=0.8 s达到稳定状态;偏航角Yaw的超调量依然比较大但调整时间变小为t=2 s,为可接受范围。在整个训练过程中,系统的目标函数值迅速衰减且单调递减。
4 PID神经网络位置控制器的设计
四旋翼飞行器控制系统的目标是实现四旋翼飞行器在地面坐标系下的定点飞行,四旋翼飞行器由起始点飞行到达目标点后悬停在目标点。为达到控制目标,设计双闭环控制系统,将整个系统分成内环控制和外环控制2部分。整个控制系统的结构框图如图6所示,系统的输入为目标位置(X,Y,Z),内环部分主要负责控制四旋翼飞行器的飞行姿态,即飞行器的3个欧拉角(Pitch,Roll,Yaw)。外环部分负责控制飞行器的坐标位置,即在地面坐标系中的三轴线位移(X,Y,Z)。

图6 Simulink下建立的控制系统框图
在Simulink中,利用工具模块建立飞行器位置控制系统的模型,并利用S函数模块创建PID神经网络控制器,控制系统总结构如图7所示。

图7 控制系统总结构

从图8、图9可知,飞行器在t=4 s时到达(1,1,1)位置并稳定,其中,X轴与Y轴变化比较缓慢平滑,而Z轴开始先下降然后再上升到指定位置,这是由于三轴之间线速度的变化互相耦合,仿真证明位置变化Z轴的耦合作用最强。
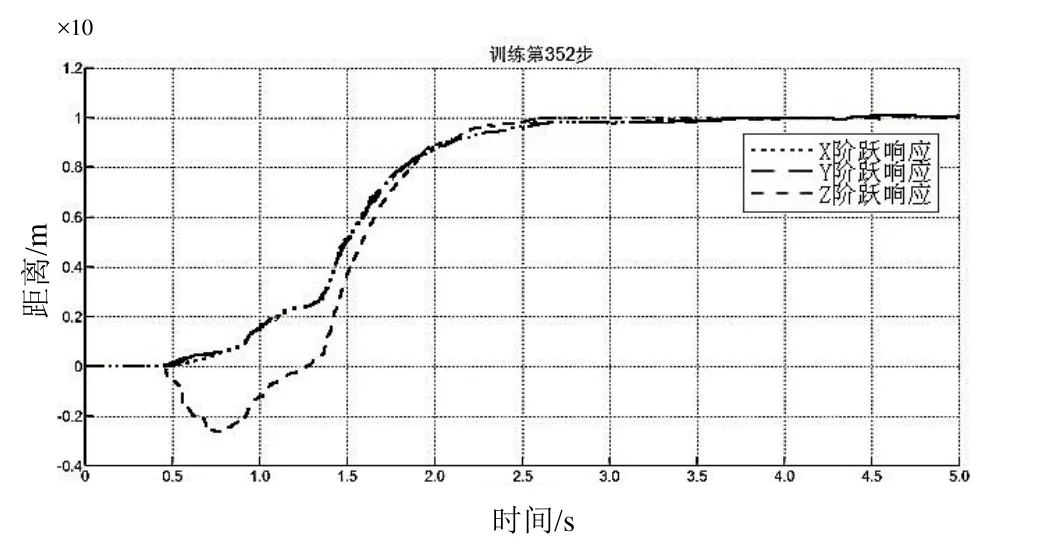
图8 训练352步后的输出
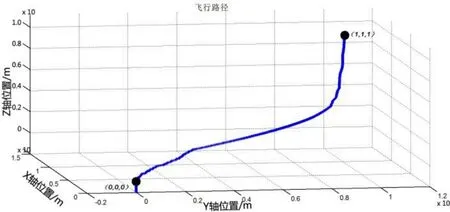
图9 位置输出三维图
5 结语
四旋翼飞行器系统是一个非线性、强耦合的多变量系统,要建立精确的数学模型非常困难,在飞行过程中会引入很多不确定的因素,传统的控制方法均采用线性化后的模型作为控制仿真对象,参数整定非常麻烦而且不精确。因此,采用PID神经网络技术设计飞行控制器,采用经典PID参数初始化网络,通过训练后,控制器能对飞行器进行解耦控制,使系统具有良好的性能,优于传统PID控制效果。
四旋翼飞行器的研究是一项多学科交叉的课题,所涉及的知识甚广,鉴于时间有限,本文只对飞行控制算法进行基础研究,未来进一步的研究将在联合仿真平台中加入更多的非线性因素,使仿真模型更接近真实工况下的物理模型。
[1] 洪森涛,金智慧,李志强.四旋翼飞行器建模及姿态稳定性分析[J].电光系统,2008(2):34-37.
[2] 聂博文.微小型四旋翼无人直升机建模及控制方法研究[D].长沙:国防科技大学,2006:11-13.
[3] 岳基隆,张庆杰,朱华勇.微小型四旋翼无人机研究进展及关键技术浅析[J].电光与控制,2010,17(10):46-51.
[4] 姚元鹏.四旋翼直升机控制问题研究[D].哈尔滨:哈尔滨工业大学,2007.
[5] 钟佳朋.四旋翼无人机的导航与控制[D]. 哈尔滨:哈尔滨工业大学,2010:12-15.
[6] 舒怀林,郭秀才,舒杰磊.注塑机料筒多段温度PID神经网络解耦控制系统[J].计算技术与自动化,2004,23(4):55-57.
[7] 舒怀林.PID神经元网络及其控制系统[M].北京:国防工业出版社,2006.2.
[8] 胡锦添,舒怀林.基于Adams与Matlab的四旋翼飞行器控制仿真[J].自动化与信息工程,2012,33(5):25-28.
[9] Shu Huailin. PID neural network control for complex systems[C]. Proceedings of International Conference on Computational Intelligence for Modelling, Control and Automation (CIMCA99’), IOS Press. 1999,2: 166-171.
舒怀林,男,1954年生,博士,教授。主要研究领域:工业自动化、计算机控制、神经网络控制、模糊控制。
Research on Quadrotor Control Algorithm Based on PID Neural Network
Hu Jintian1Shu Huailin2
(1. Guangzhou Research Institute of O-M-E Technology
2. School of Mechanical and Electrical Engineering, Guangzhou University )
To solve the problem of Quadrotor’s attitude and position control, the control algorithm based on PID neural network is proposed. In this paper, the mathematical model of Quadrotor is set up, and the associated simulation platform of Quadrotor is imported. The PID neural network attitude controller which can achieve good control effect after training is designed by using Matlab. The PID neural network position controller is designed and trained. The simulation result shows that the algorithm is better than the traditional PID algorithm.
胡锦添,男,1986年生,硕士。主要研究领域:机电控制中的人工智能、机器人。E-mail: jthu4alex@163.com
Key Works:Quadrotor; PID Neural Network; Attitude Control

