广东省北江流域坡向与海拔对汛期降水量的影响

梁胜华 张 灵 千怀遂 李明霞 邹小硕

(广州大学地理科学学院,广州 510006)



广东省北江流域坡向与海拔对汛期降水量的影响

梁胜华*张 灵 千怀遂 李明霞 邹小硕

(广州大学地理科学学院,广州 510006)

利用1956—2000年广东省北江流域40个水文站逐月降水量资料，统计北江流域汛期降水量与山地坡向及海拔高度的关系特征。利用地理加权回归(GWR)方法消除站点空间位置不同带来的宏观地理因子影响后，进行多年平均汛期降水量随海拔高度变化的相关分析，根据其点聚程度分区，研究降水量随海拔高度的变化规律。结果表明：广东省北江流域汛期降水量总体上呈纬向空间分布，由南至北逐渐减少，其中多雨区位于北江流域的东南部；在流域中部的英德至流域南部的清远之间的干流附近存在稳定的多雨中心。4个子区域最大降水量高度不同，由南至北分别为77.3 m，408.4 m，353.6 m和376.9 m，相对应的最大降水量分别为1566.2 mm，1467.4 mm，1295.9 mm 和1151.5 mm。广东省北江流域汛期降水量变差系数由西南至东北依次增大，说明降水量的年际变化呈北大南小的空间分布规律。

北江流域； 坡向； 海拔； 最大降水量高度

引 言

降水量随海拔高度的变化受多种因素影响，对多山岭复合山系而言，尤为突出。对于地形性降水的空间分异研究，20世纪70—80年代[1-3]人们多采用单一山坡的不同海拔高度的气象观测资料进行研究，用多元回归分析方法建立它们之间的稳定性关系[4-9]。尽管也考虑了宏观地理因子的影响，但相关方法很难直接用于多山岭复合山系研究中。且仅从回归分析方法研究地形与降水量之间的关系，尚不足以直观说明地形对降水量影响的空间分布特征[10]。近10年，人们结合数字高程模型及空间插值的方法，将降水量由离散点插值为连续分布的面状信息研究山区降水量随海拔高度的变化[11-13]，但因为站点的位置及密度均受地形条件制约[14]，当观测资料稀疏且地形复杂时, 插值准确度难以保证。同时，也未考虑山岭之间的相互影响，因此，对于多山岭复合山系的研究来讲，仍是个缺憾。

本文在利用克里金插值法对降水量进行插值之前，对影响降水量空间分布的宏观地理因子进行地理加权回归(GWR)处理，对降水量和地形因子进行回归分析，根据降水量的空间分布特征、降水量随海拔高度变化的不同参数，将地形按不同坡地方位进行分区[15-17],利用分区站点连片的原则和不同分区的降水量的连片结果加以验证。

1 研究区域和资料处理

北江是珠江流域第二大水系，流域面积为46710 km2(其中广东省内部分占流域总面积的92%)， 主要流经广东省韶关、清远地区，流域内大部分为山区和丘陵。流域降水量多、强度大，降水多集中在汛期的4—9月，其汛期降水量可占全年降水量的70%以上[18]。以前涉及北江流域降水量的研究大都将北江流域嵌套在大尺度范围内[19-24]，对北江流域降水量特征的研究鲜见报道。

本文研究区域为广东省内的北江流域(图1)，1956—2000年降水量资料来自北江流域的40个水文站，30 m×30 m分辨率的数字高程模型(DEM)数据源自www.csdb.cn.

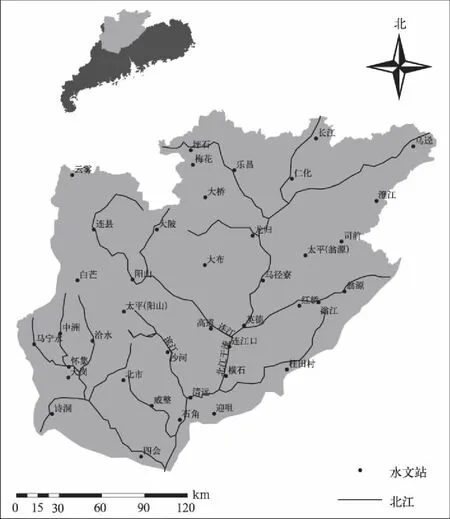
图1 广东省北江流域水文站分布 Fig.1 Hydrological site map in Beijiang River Basins of Guangdong Province

2 拟合方法与结果分析

山地上任意一点降水量均在地形因素R(α,β)、地方海拔高度R(h)和宏观地理因子R(φ,θ)共同影响下形成[25]，

R=R1(α,β)+R2(h)+R3(φ,θ)+ε。

(1)

式(1)中，R为山地任意一点降水量，α为坡度，β为坡向，R1为坡度与坡向影响的降水量，h为海拔高度，R2为海拔高度影响的降水量，φ和θ分别为纬度和经度，R3为纬度和经度影响的降水量，ε为随机误差。

2.1 坡度因子处理方法

坡度表示地表面的陡缓程度，其对降水量的影响主要体现在对气流的抬升作用方面。通常，坡度越大，风速的垂直梯度越大，对气流的抬升作用也越大，导致降水的垂直梯度变化也增加。对研究区域地形分析表明：该流域坡度均较平缓，平均坡度仅为13°，坡度小于45°的区域占研究区域的98.9%左右，所选的40个站除白芒站坡度高于45°以外，其余站点均小于45°。傅抱璞[26]指出，当α在0°～45°之间变化时，无论是在背风坡面还是迎风坡面，坡度对降水量的影响在实际计算中可以忽略不计，故在本文分析中对坡度因子(α)不予考虑。

2.2 宏观地理因子处理方法

由于各观测站分布于不同的地理位置，利用不同地理位置的海拔高度和降水量反映两者关系，由此得出的结论与实际情况会有较大出入[27]。为了尽可能消除地理因子带来的影响，利用地理加权回归模型[28]将空间位置嵌入降水量资料中，以某站所在的地理位置到其他各站的地理位置的距离作为权函数，对降水量进行局部加权最小二乘方法逐点估计。即通过地理加权，使各观测站近似地被看作处于同一地理位置，以此消除宏观地理因子的影响。

在地理加权回归模型中，特定区域的回归系数不再利用全部信息获得的假定常数，而利用邻近观测值的子样本信息进行局域回归估计，是随空间上局部地理位置变化而变化的变数。通过各地理位置上的参数估计值随地理位置的变化情况，可以非常直观地探讨空间关系的非平稳性。

本文以截尾型的bi_square函数为权函数，利用交叉验证方法(CV)选择最优带宽，以海拔高度为解释变量，多年平均汛期降水量为被解释量，对降水量进行地理加权回归。GWR模型可表示为

Yi=β0(μi,vi)+β1(μi,vi)Xi+εi，

i=1，2，3，...，20。

(2)

式(2)中，Yi为第i个站的多年平均汛期降水量,Xi为第i个站的海拔高度,(μi，vi)为经度和纬度，β0(μi，vi) 为多年平均汛期降水量随空间位置即经、纬度发生的变化，β1(μi，vi)为多年平均汛期降水量随海拔高度的变化率。

经GWR回归后模型的拟合优度(R2)为0.71，条件函数显著低于30，模型效果较好。

2.3 坡向因子处理方法

坡向指地形坡面朝向，风向与山脉迎风坡夹角越大，气流的辐合上升作用也越大，山的迎风坡为多雨中心。相应地，盛行风的背风坡则形成了降水稀少、气候干燥的少雨区。因此，山体所处的不同坡向位置，会对降水量大小产生影响。研究山地坡向对降水量的影响，首先要进行坡向划分，但在宏观区域研究中，要对每一山体进行坡向划分几乎不可能。研究表明，不同坡向对降水影响的差异主要体现在降水量随海拔高度的变化率上[17]。因此，如果根据降水量随海拔高度变化的不同参数确定山体的不同方位和坡向[29]，那么坡向对降水的影响将隐含于分区之中。

2.4 分区拟合结果

2.4.1 分区拟合步骤

首先将GWR估算的降水量与相应的海拔高度点绘在坐标图上(图2)，以其点聚的相关程度作为划分标准。由图2可看出，有4条变化率显著不同的降水量随高度变化曲线，4条曲线的拟合优度由上至下分别为0.69，0.88，0.70以及0.65，拟合效果尚可。

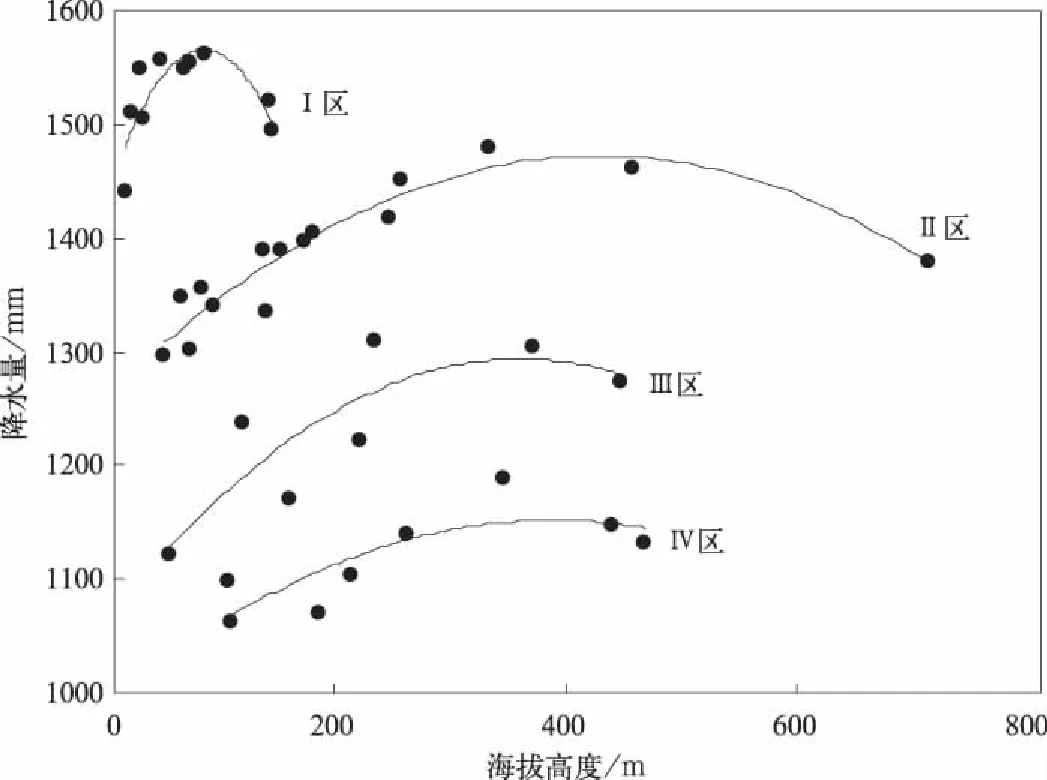
图2 GWR估计的广东省北江流域多年平均汛期降水量与海拔高度相关Fig.2 Correlation diagram of multi-year mean flood season rainfall to altitude in Beijiang River Basins of Guangdong Province

由图2可初步认为，按照坡向差异大致可分为4个子区域，分别为Ⅰ，Ⅱ，Ⅲ，Ⅳ区。为进一步验证子区域划分的合理性，利用克里金法插值得到降水量分布图(图3)。由图3可知，降水量由东南至西北依次递减，且经对图2中的4条曲线求最大值后发现，4条曲线的最大值由Ⅰ区至Ⅳ区分别为1566.1 mm，1467.4 mm，1295.9 mm和1151.4 mm，这4个最大值反映的是研究区域降水量由东南至西北递减的形式。由此考虑将Ⅱ，Ⅲ，Ⅳ区插值后的最大降水量作为分界线划分出4个区域，检验4条曲线的相关点是否均有规律地分布在相对集中的区域内。由图3可知，这4条曲线的相关点绝大多数有规律地分布在按曲线最大值划分的4个子区域内。

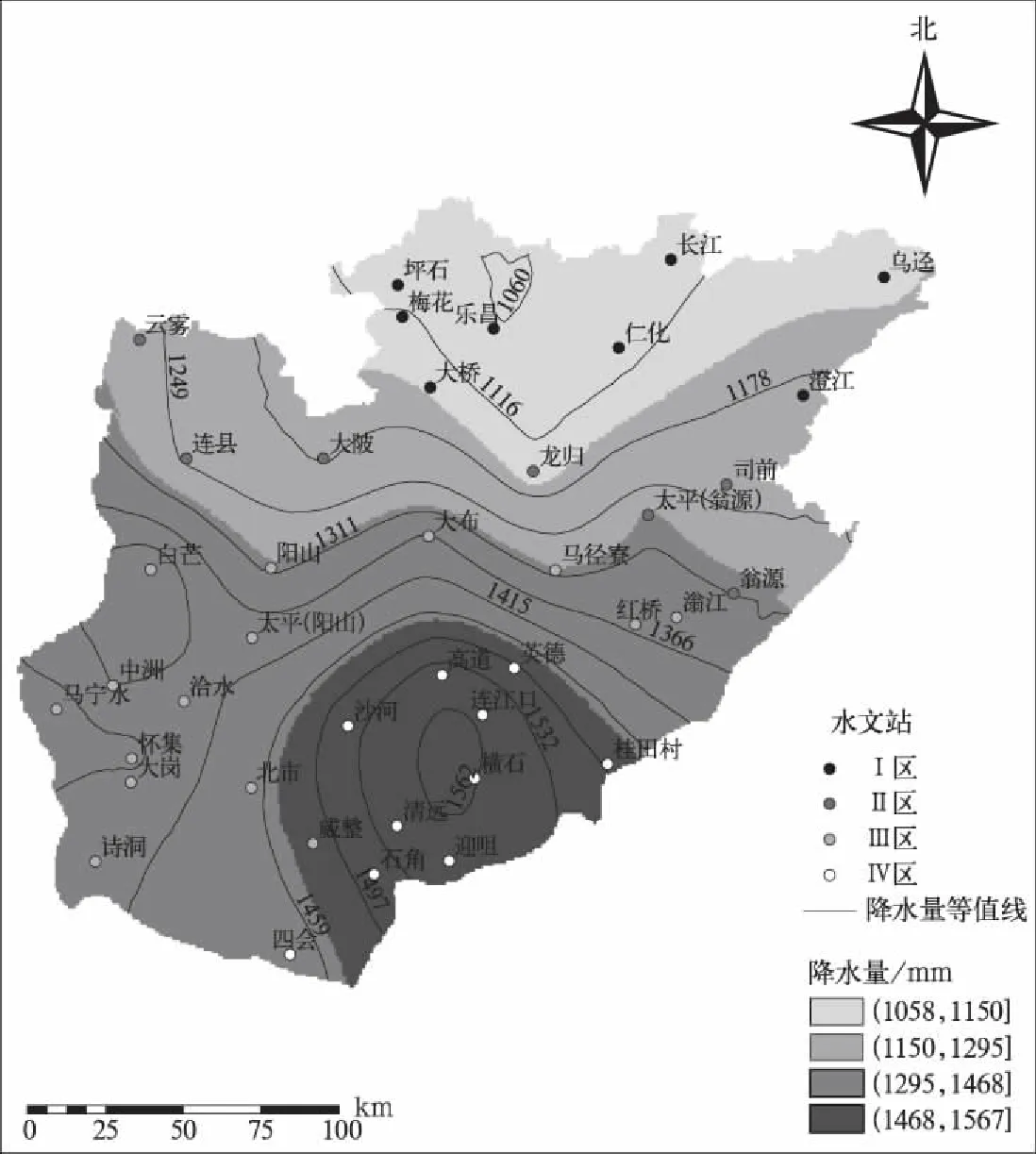
图3 广东省北江流域多年平均汛期降水量分布及分区Fig.3 Multi-year mean flood season rainfall and partition in Beijiang River Basins of Guangdong Province

2.4.2 插值结果验证

本研究采用交叉验证方法对插值结果进行分析验证，即移去1个已知水文站，用其他站点资料估计该站情况以检验插值精度的方法。研究过程中,对40个站的插值结果进行全交叉验证，运用平均绝对误差、最大偏离、最小偏离和均方根误差作为检验参数。平均绝对误差、最大偏离和最小偏离表示的是预测值与真值之间的残差大小，残差值的大小可用于衡量源数据的预测值与真值之间的一致性，残差值越小，表明预测值与真值之间的误差越小；均方根误差用来衡量预测值同真值之间的偏差，均方根误差越小，预测值就越接近于真值。经检验，平均绝对误差、最大偏离、最小偏离和均方根误差分别为-1.78 mm，141.18 mm，1.30 mm和58.02 mm。即采用克里金法插值本研究区域内的降水量分布，插值效果较好,可以得到较精确的降水量预测值。

2.4.3 拟合结果分区特征

从整体上看，研究区域位于南岭南侧，相对于由南海而来的暖湿夏季风为迎风坡，且在北江附近为一向南张开的喇叭口凹陷区。从南岭向南伸出几条山岭，其中北江西侧平行分布着西北—东南走向的罗壳山和大东山，北江东侧为平行分布的青云山和滑石山。大东山和滑石山之间的距离非常狭窄，它们与南岭主体合围而成韶关盆地；罗壳山和青云山之间则为较宽阔的平地。因此，相对于夏季风而言，可将该区域的地形分为南岭主体迎风坡区、大东山—滑石山迎风坡区、大东山—滑石山背风坡和韶关盆地地区、北江下游平地区这4个子区域。

无论是从坡向分区还是依据汛期降水量特征的划分均表明研究区域可划分为4个子区域。经地理加权回归后整个研究区域可看作是具有同一经纬度的山体，又由于该区域按坡向分区，则可将4个子区域分别视为该山体所在的不同坡向区域。4个子区域各有不同的区域和降水量特征。

Ⅰ区位于北江流域下游(图4a),平均坡向为178°，平均高程为172.3 m，平均坡度为10.8°，且背靠罗壳、大东、滑石、青云4座山。Ⅰ区夏季盛行来自海洋的东南季风，空气高温、高湿且接近饱和，微凸地貌抬升、前方山地阻挡以及喇叭口地形辐合效应使之成为一个稳定的多雨中心区。Ⅰ区汛期最大降水量位于山麓地带77.3 m处，其最大汛期降水量为1566.1 mm。最大汛期降水量出现在北江干流与其两条支流(连江和滨江)的汇合处，Ⅰ区的高程明显高于四周，故当暖湿气流途径此处时，遇到此凸地的阻滞，在此地形成降水量峰值。

Ⅱ区处于北江中游地区(图4b)，暖湿气流到达Ⅱ区时，虽然水汽含量已有所下降，但由于Ⅱ区的平均海拔相对较高，平均高程为346.8 m，平均坡度为13.9°，均高于Ⅰ区，且Ⅱ区西面有西北—东南走向的罗壳山，背靠大东山，处于山岭的迎风坡。当气流进入该地时，由于喇叭口效应，引起气流辅合上升，促进对流发展形成为云雨。所以Ⅱ区汛期降水量虽较Ⅰ区有所下降，但总的来说仍较为充足。汛期最大降水量高度位于Ⅱ区的408.4 m 处，汛期最大降水量为1467.4 mm。

图4 广东省北江流域分区高程 (a)Ⅰ区,(b)Ⅱ区,(c)Ⅲ区,(d)Ⅳ区Fig.4 The partition elevation map in Beijiang River Basins of Guangdong Province(a)Area Ⅰ,(b)Area Ⅱ,(c)Area Ⅲ,(d)Area Ⅳ

Ⅲ区位于北江中上游(图4c)，具有在整个研究区域内最高的平均高程450.8 m以及最高的平均坡度14.3°，且有广东最高峰石坑崆。虽然有高山阻挡所引起气流抬升、对流加强的因素，但由于暖湿气流经Ⅰ区和Ⅱ区后，水汽含量已减少，且该区位于大东山—滑石山背风一侧的韶关盆地，从Ⅱ区到Ⅲ区，降水量降低非常明显。汛期最大降水量高度位于Ⅲ区的353.5 m处，汛期最大降水量为1295.9 mm。

Ⅳ区位于北江上游的南岭南麓(图4d)，平均坡向为180°，Ⅳ区山体的走势大多为东—西走向为迎风坡，且海拔较高，平均高程为411.8 m。平均坡度为13.4°。Ⅳ区降水量较少，其汛期最大降水量仅为1151.4 mm，位于该区的376.9 m处。Ⅳ区汛期降水量随海拔高度变化平缓，说明汛期降水量在Ⅳ区的不同海拔高度上变化不大，且为少雨中心，主要因为暖湿气流到达此处时，水汽含量较Ⅰ，Ⅱ，Ⅲ区显著减少，致使海拔高度变化也不足以使该区降水量出现较大起伏。

2.5 降水量年际变化特征

不同特征高度的平均降水量具有不同的空间分布变化特征，但不同特征高度降水量是否也会体现出相应的年际气候变化特征，本文利用降水量变差系数反映降水量年际变化的相对大小。若变差系数大，则该点年降水量变化大，不稳定；若变差系数小，则各年的降水量变化不大，相对平稳。

变差系数CV的计算利用地理加权回归后的40个站的汛期降水量标准差与其平均值的比值获得，结果显示：1956—2000年40个站CV介于0.190至0.270之间，最大值位于乌迳，最小值位于北市附近。由广东省北江流域汛期降水变差系数的分布(图5)可知，北江流域年汛期降水变差系数由西南至东北依次增大，说明降水的年际变化呈北大南小的空间分布规律，这也与北江流域北部多山地南部地势较平的地形有关。

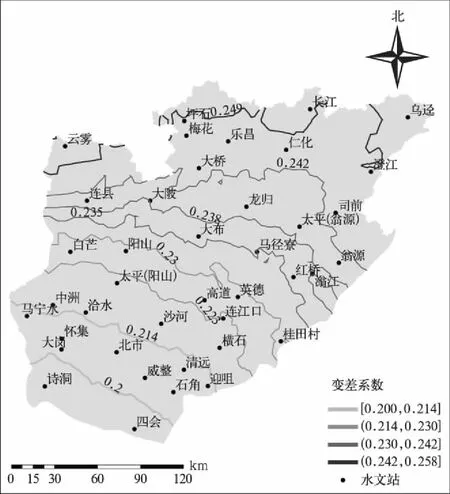
图5 1956—2000年广东省北江流域汛期降水量变差系数分布Fig.5 CV of flood season rainfall in Beijiang River Basins of Guangdong Province from 1956 to 2000

若将CV与海拔高度进行相关分析，则可看出在不同特征高度处降水量的年际气候变化特征。经计算所得的结果并未呈现出明显的相关关系，这与山岭对气流的拦截效应和暖湿气流的强度有关。

3 结论与讨论

本文利用广东省北江流域40个水文站逐月降水量资料，分析该区域降水量空间分布特征：

1) 多年平均汛期降水量随海拔的变化呈明显的区域分异特征，总体呈纬向空间分布，由南至北可划分出4个子区域，4个子区域的最大降水量高度分别为77.3 m，408.4 m，353.6 m和376.9 m，相对应的最大降水量分别为1566.2 mm，1467.4 mm，1295.9 mm和1151.5 mm。

2) 1956—2000年汛期降水量的年际变化具有明显的区域分异特征，降水量变差系数由南向北逐渐变大，最大值(0.270)位于乌迳，最小值(0.190)位于北市附近，总体呈北大南小的空间分布规律。

广东省北江流域降水量随海拔变化的纬向空间分布规律，主要与区内的地形具有明显的区域分异特征相关，由南至北分别为北江下游向南张开的喇叭口凹陷区、由大东山和滑石山与南岭主体合围而成的韶关盆地、大东山—滑石山迎风坡区以及南岭主体迎风坡区等4个子区域。

1956—2000年广东省北江流域汛期降水量呈北大南小的空间分布规律，一方面与该区域北部山地海拔较高、南部海拔较低地形因素有关，另一方面与山岭对气流的拦截效应和暖湿气流的强度有关，当暖湿气流较弱时，南部山岭的拦截效应相对比较强，南部山岭的拦截使暖湿气流的水汽含量减少，而使该区域北部的降水量年际变化增大。

[1] 蒋忠信.山地降水垂直分布模式讨论地理研究,1988,7(1):73-78.

[2] 傅抱璞,李兆元.秦岭山地的气候特点.陕西气象,1983,11(1):1-11.

[3] 袁育枝.河北山地降水的垂直分布.气象,1979,14(10):34-36.

[4] Basist A, Bell G D, Meentemeyer V. Statistical relationships between topography and precipitation patterns.JClimate,1994,7(9):1305-1315.

[5] Goodale C L,Alber J D,Ollinger S V.Mapping monthly precipitation,temperature,and solar radiation for Ireland with polynomial regression and a digital elevation model.ClimateRes,1998,9(1):35-49.

[6] Naoum S,Tsanis I.Orographic precipitation modeling with multiple linear regression.JHydrolEng,2004,9(2):79-102.

[7] 陈贺,李原园,杨志峰,等.地形因素对降水分布影响的研究.水土保持研究,2007,14(1):119-122.

[8] 舒守娟,王元,熊安元.中国区域地理、地形因子对降水分布影响的估算和分析.地球物理学报,2007,50(6):1703-1712.

[9] 覃志年,胡娅敏,陈丽娟.广西夏季降水的多时间尺度特征及影响因子.应用气象学报,2013,24(5):565-575.

[10] 任国玉,吴虹,陈正洪.我国降水变化趋势的空间特征.应用气象学报,2000,11(3):322-330.

[11] 张升堂,康绍忠.基于拉格朗日插值法修正地形影响的分布式降水模型研究.水文,2004,24(6):6-9.

[12] 周锁铨,孙琪,肖桐松,等.长江中上游区基于GIS的不同时间尺度降水插值方法探讨.高原气象,2008,27(5):1021-1034.

[13] 庄立伟,王石立.东北地区逐日气象要素的空间插值方法应用研究.应用气象学报,2003,14(5):605-615.

[14] 徐成东,孔云峰,仝文伟.线性加权回归模型的高原山地区域降水空间插值研究.地球信息科学,2008,10(1):14-19.

[15] 伍立群,李学辉.高山地区年降水量随高程变化分析.云南地理环境研究,2004,16(2):4-7.

[16] 赵成义,施枫芝,盛钰,等.近50 a来新疆降水随海拔变化的区域分异特征.冰川冻土,2011,33(6):1203-1213.

[17] 王菱.华北山区坡地方位和海拔高度对降水的影响.地理科学,1996,16(2):150-158.

[18] 邹正欣,许晓明.广东北江流域水资源可持续利用存在的问题及解决对策.黑龙江科技信息,2008,15(7):119;64.

[19] 纪忠萍,高晓容,谷德军,等.广东低温阴雨的低频振荡及环流特征.应用气象学报,2013,24(1):32-42.

[20] 余功梅.华南地区近40年降水的气候特征.热带气象学报,1996,12(3):61-65.

[21] 谢炯光.广东省前汛期降水分布趋势的分析与预测.应用气象学报,1997,8(4):68-75.

[22] 马慧,王谦谦,陈桢华.华南前汛期降水异常的时空变化特征.高原气象,2006,25(2):325-329.

[23] 黄茂栋,廖仕湘,杨立洪.广东汛期降水的时空分布特征.广东气象,2008,30(6):33-36.

[24] 张婷,魏凤英,韩雪.华南汛期降水与南半球关键系统低频演变特征.应用气象学报,2011,22(3):265-274.

[25] 刘占明,陈子燊,路剑飞,等.广东北江流域降水时空分布及其与Nino3区SST相关性分析.自然资源学报,2013,28(5):786-798.

[26] 傅抱璞.地形和海拔高度对降水的影响.地理学报,1992,47(4):302-314.

[27] Leung Y,Mei C L,Zhang W X.Statistical tests for spatial non-stationariy based on the geographically weighted regression model.EnvironmentandPlanning,2000,32(1):9-32.

[28] Brunsdon C F,Fotheringham A S,Charlton M.Geographically weighted regression modeling spatial non-stationarity.TheStatistician,1998,47(3):431-443.

[29] 廖菲,洪延超,郑国光.地形对降水的影响研究概述.气象科技,2007,35(3):309-316.

Effects of Slope and Altitude on the Precipitation During the Flood Season in Beijiang River Basins of Guangdong Province

Liang Shenghua Zhang Ling Qian Huaisui Li Mingxia Zou Xiaoshuo

(InstituteofGeographicalScience,GuangzhouUniversity,Guangzhou510006)

To study the spatial differentiation phenomena of precipitation in composite-mountain system, the relationship between the mountain slope, altitude and the precipitation of Beijiang River Basins during the flood season is analyzed with the method of multi-factor separation, using monthly precipitation data from 1959 to 2000 collected from 40 hydrologic stations. In order to eliminate effects of macro geographical factors, the data heterogeneity caused by different locations of hydrologic stations is resolved by using the geographically weighted regressing (GWR) method. The correlation diagram of the multi-year mean precipitation and the altitude is constructed according to the evaluation from GWR, and it is divided into four sub-areas based on the point scattering. On the basis of the division, the correlation between the precipitation change and altitude is researched. According to the changing rate of precipitation with the altitude, Beijiang River Basins are partitioned, and effects of warm air through the upstream and downstream on precipitation change with altitude are studied.

The result shows that the distribution of the multi-year mean precipitation during the flood season in Beijiang River Basins is perpendicular to parallel and it decreases from the south to the north. The rainy area is in the southeast of the basin and the mainstream from Yingde to Qingyuan is a stable rainy center. With the change of altitude, precipitation curve shape of the composite-mountain system can be summarized as the parabolic type. The variation of precipitation with the change of altitude in composite-mountain system is related to the precipitation interception effect of warm air through the upstream and downstream of the ridge. Varying characteristics of the average precipitation during the flood season in Beijiang River Basins demonstrate the obvious regional differentiation, it can be divided into four sub-regions, and there are different maximal precipitation in different sub-areas. From the south to the north, altitudes are 77.3 m, 408.4 m, 353.6 m, 376.9 m and the maximum precipitation are 1566.2 mm, 1467.5 mm, 1295.9 mm, 1151.5 mm, respectively. The precipitation during the flood season in Beijiang River Basins gradually increases from south to north, which means that the annual variation of precipitation presents spatial distribution regularities, bigger in north and smaller in south. This is associated with interception effect of mountains to the airflow and warm air strength. When the warm air is stronger, the interception effect on airflow upstream mountain water is relatively small. When the warm air flow is weak, the interception effect of upstream mountains is relatively strong.

Beijiang River Basins; slope; altitude; maximum precipitation altitude

10.11898/1001-7313.20150309

国家自然科学基金项目(51210013)

梁胜华,张灵,千怀遂,等. 广东省北江流域坡向与海拔对汛期降水量的影响. 应用气象学报，2015，26(3)：338-345.

2014-09-19收到， 2015-01-05收到再改稿。

* email: 947863343@qq.com