关于集总参数电路抽象原则的一点思考

姚缨英，李海红

(浙江大学电气工程学院，浙江杭州310027)

0 引言

国内大多数电路教材在给出集总(中)参数电路定义时均采用类似于“电路的各向尺寸远小于电路周围电磁波的波长时，电路参数的分布性对电路性能的影响并不明显，从而可以近似地用集中的电阻、电容和电感作为电路的参数，即认为能量损耗、电场储能和磁场储能这三种过程是分别集中在电阻元件、电容元件和电感元件中进行的。由这些理想的集中参数元件构成的电路称为集中参数电路”或者“端钮上的电压、电流为确定值”的说法[1-5]。

因为这些描述不够具体，作为能否采用集总参数电路模型抽象的依据，常常有学生提出疑问或异议:电磁场中的变量和怎样转换成为电路中的变量u和i?l≪λ是区分集总参数电路和分布参数电路的唯一依据?教材［6］虽然已附加了和作为集总参数电路抽象的限制条件，其由来又如何?另外，教材中基尔霍夫定律是直接给出的，但大多数教材都补充解释说KCL是电流连续性的表现(或称电荷守恒)，KVL是电压与路径无关这一性质的反映(或称能量守恒)。那么，能否从时变场的麦克斯韦方程推导出基尔霍夫定律?虽有一些教材在恒定电流场中对此过程的推导有过描述，但因为是静态场所以难免牵强[7]。再者，传输线理论本质上是基于电报方程的分布参数电路理论，即所谓的电磁场方程的“路”理论。采用了对一维空间尺度离散化的方法，仍然用电路的参数和模型来描述。那么分布参数电路与集总参数电路的关系又是怎样呢?能否按电磁场理论推出这两种路问题的数学模型?

1 集总参数电路抽象原则

1.1 集总参数系统的基本假设

众所周知，麦克斯韦方程组是关于电磁现象规律性的数学描述，应用范围很广。当客观电磁现象与过程被约束在一维的“电流通路”之中时，通过理想化电路模型的构造，即可简明有效地应用基尔霍夫定律解决客观电磁现象与过程的分析。那么，我们必须给出进行该简化的依据，笔者认为，这就是集总电路抽象原则。

根据文献[8]陈述的集总事物原则，本文定义集总参数系统基于下述三个基本假设:

(1)系统中每个元件的净增电荷总是零;

(2)系统中的元件之间没有磁耦合(磁耦合可发生在元件内部);

(3)电效应在瞬间贯穿整个系统。

1.2 集总参数元件的抽象原则

集总参数系统中的元件称为集总参数元件。可见，集总系统是由集总元件互连组成的。并且在集总系统内集总元件之间的电磁场相互无影响，系统与外部也无电磁交换，是电磁能量独立的系统。凡不满足上述假设条件的系统称为分布参数系统，需要用电磁场理论进行分析。

将上述假设具体化，则集总参数元件的抽象约束原则是:

(2)在所有时刻，元件与外部任何闭环交链的磁链的变化率为零，即ψ/t=0;

(3)感兴趣的时间范围必须远长于电磁波在元件内部传输的时间延迟，即系统最大尺度远小于系统信号的最大波长(l≪λ);

满足前两个约束之后，元件除了通过其端钮上的电压和电流外，相互之间不发生关系。同时保证流入端钮的电流唯一并流出端钮，并确保端钮上定义的电压唯一。约束(3)是具有空间尺度的器件质点化的前提条件。事实上，满足上述两个条件的电磁场是似稳场，而似稳场的宏观判据是约束(3)。

1.3 电路抽象示例

如果定义一个元件，如图1所示。

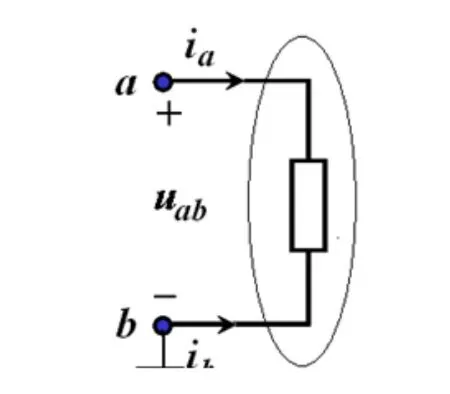
图1 电路抽象示例

该元件有两个端钮a和b，在每个端钮上有流入的电流ia和ib，元件两端电位(电势)分别为φa和φb。并假设s为包围该元件的闭合曲面，端钮导线的截面积分别为sa和sb。

根据约束的假设(1)，由麦克斯韦方程可知全电流(包含传导电流和位移电流)是连续的，也就有式中为在导体中流动的传导电流为变化的电场所对应的位移电流。将麦克斯韦方程组中的电高斯定理q代入全电流连续方程，则有今由约束假设(1)可得，/t=0。即意味着0，故电流连续性归结为

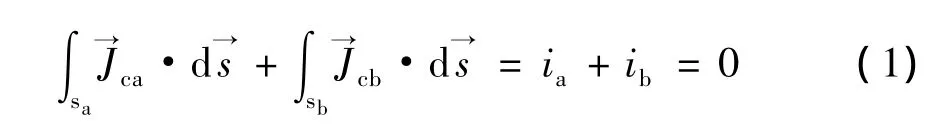
从而有 ia=-ib。而表明随时间变化的磁场是磁准静态场。这样才可以用dq/dt=i来定义传导电流。

从上面两个假设不难看出，它们都隐含了一个条件，那就是准静态场。所谓的准静态场是满足似稳条件l≪λ(或t=l/c≪λ/c)的动态电磁场。含义很明确，就是脱离了场源的电磁波在该元件中的传播时间t远小于该信号对应的变化周期T。这意味着，不必考虑信号传播的电磁场滞后效应，所以元件上各处的电磁现象是同时变化的，从而可将其作为一个空间上的质点看待，将电磁以及材料特性都用相应的特征参数量予以表征。

假设图1所示的椭圆圈内物体是一段长为l具有均匀截面积S的导体，如图2(a)所示。其中电磁场满足似稳场条件，导电材料的电导率为γ，可知有

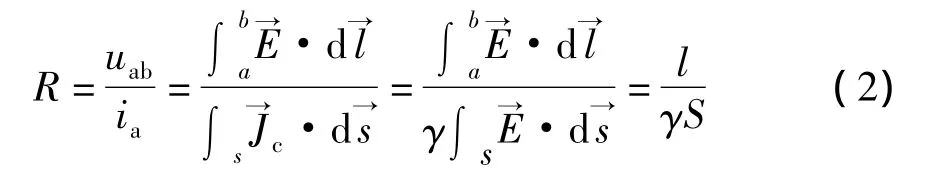
关系式uab=Ria就是传导电流在导体中电磁表征的数学陈述(也称为数学模型)。关系式被称为特性方程，对应的曲线即称为特性曲线，用电路符号R来表示，如图2(b)。

上述过程就是理想电阻元件的抽象过程。依此原理，即可类比地定义所需的模型元件。

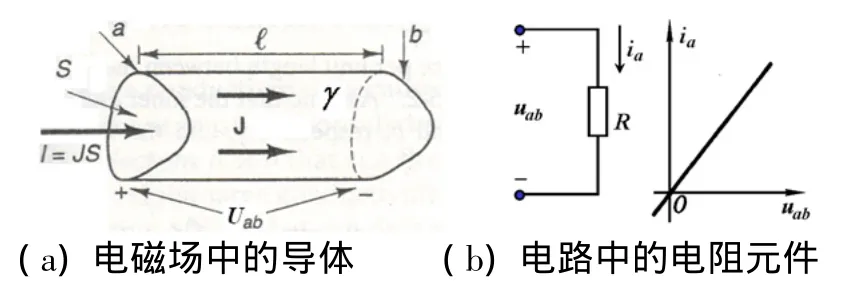
图2 导体及其电路抽象

2 基尔霍夫定律的推演

依据上述集总参数电路系统的假设，在按照集总电路抽象原则得到的电路中0，因此，很容易仿照恒定场推导出沿任意路径有，此时电场为保守场，做功与路径无关，也就是电压具有单值性。

3 分布参数电路模型的限制条件

3.1 分布参数电路模型

现在，我们以图3所示的长直同轴电缆为例，来分析集总参数电路和分布参数电路的推导。这里的内外导体为理想导体，半径分别为a和b，导体间充有理想介质ε和μ。麦克斯韦方程为

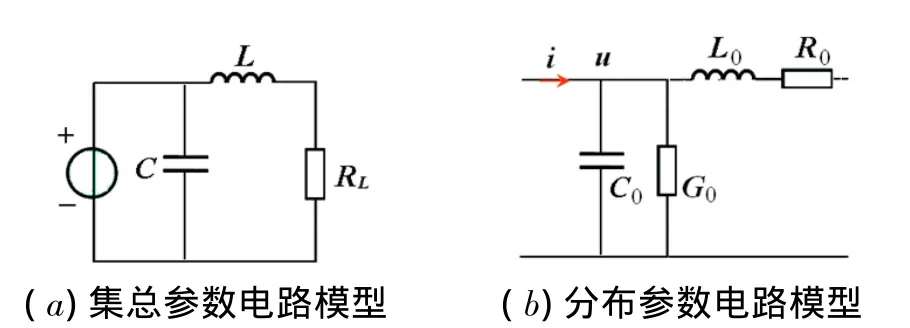
图3 长直同轴电缆及其等效电路模型

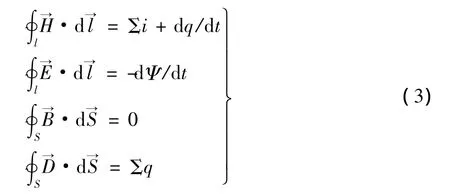
在满足集总电路抽象条件时，有dq/dt=0和dΨ/dt=0，则此时的电场与磁场均为准静态场，相互之间没有电磁耦合，即电场的方程为与静电场方程类似，其解为

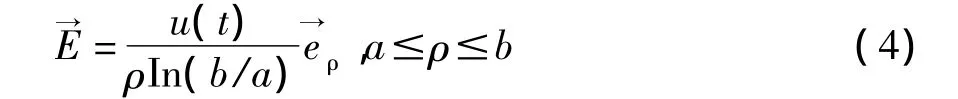
内导体表面每单位长度电荷为

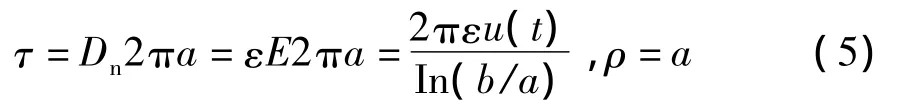
则单位长电容为C0=2πε/In(b/a)，磁场的方程为

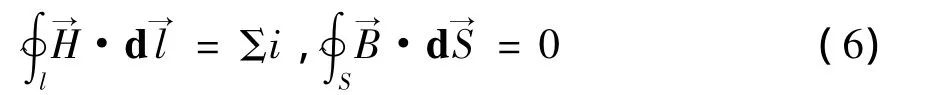
与静磁场方程类似，其解为

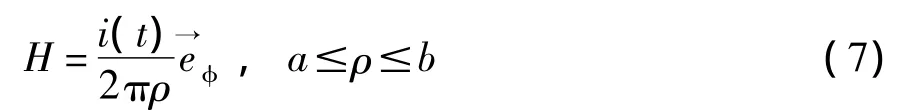
则单位长电感为L0=μIn(b/a)/2π。

此时，坡印亭矢量和穿过同轴电缆轴向任意横截面中的能流总和分别为

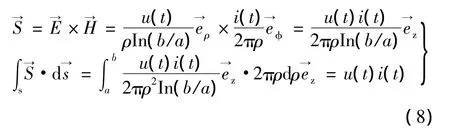
综上所述，单位长同轴电缆即可抽象为一个电容和一个电感。如果沿导线可忽略电磁波的推迟效应，则可将整个同轴电缆用图3(a)所示电路表示。

3.2 非理想导体电路

如果内外导体间的介质有损耗，则可推得对应于Us的电流场

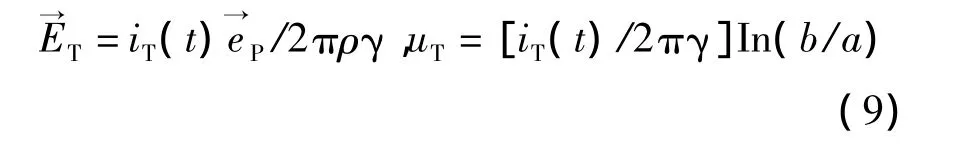
则单位长漏电导为

虽然我们推出了分别表示各单一电磁现象的集总电路元件，如C0代表内外导体间的电场储能，L0表示磁场储能，R0表示导体中的损耗，G0表示媒质损耗，但是并不能精确反映电路的结构，特别是各器件互连及与电源和负载之间的关系。

3.3 集总参数电路与电磁场分析的区别

下面我们通过对同一问题的分布参数电路建模过程来说明其间的区别。

从电磁场理论中，我们知道任何能建立静态场的导波系统必然能够维持TEM波。沿均匀传输线(z方向)传播的平面波则是TEM波，其电场和磁场具有下述形式:

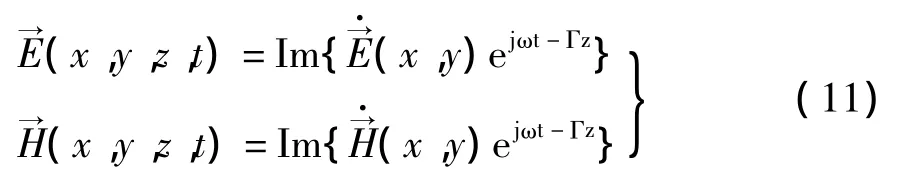
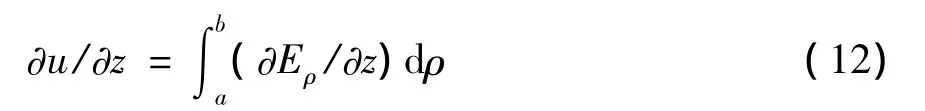
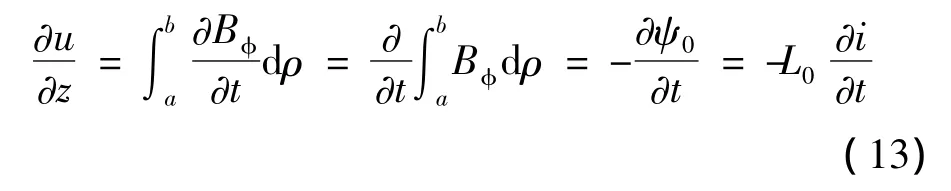
式中，ψ0表示沿z方向每单位长度中穿过的磁链，L0为单位长电感。由又因0，所以，将其代入上述积分式，可得

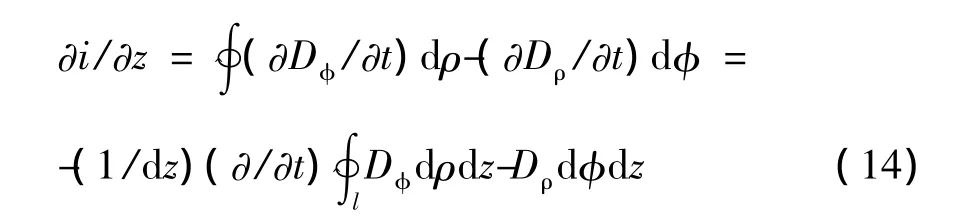
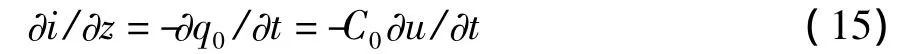
式中，C0为单位长度的电容。式(13)和式(15)就是无损耗传输线的基本方程。可见，电压电流沿线是变化的。

如果电介质有损耗，则电磁场方程除了考虑位移电流密度外，还应考虑传导电流密度。式(13)应修改为

若导线有损耗，式(2)应修改为

这就是一般情况下分布参数电路的基本方程。

3.4 推广而得的结论的局限性

事实上，上述推广而得的结论是不严格的。因为导线若有损耗，则必然有Ez分量，系统中的电磁波不再是TEM波。不过由于电场的横向分量远大于轴向分量，所以，式(16)和式(17)导得的结果和从电磁场方程组求得的解十分接近。

分布参数电路与集总参数电路的区分可以用是否具有电磁波的特征来简单判别。但是，分布参数电路模型则是在满足TEM波的特定情况下推得的。而TEM波在横截面内电场和磁场分布与相应系统的静态场分布相同，沿轴向的分布具有波动性。

4 结语

我们研究的电磁场理论与电路理论相互之间有着密切的联系，这一点在集总电路抽象的过程中尤为突出。因此，我们在教学的过程中，特别是研究性大学电类系列课程教学的过程中，应该把握适当的时机和方式强化其中的关联，强化模型化过程中的条件与限制。

[1]江泽佳，电路原理[M]，北京，人民教育出版社，1979

[2]江缉光，刘秀成，电路原理(第二版)[M]，北京，清华大学出版社，2007

[3]李瀚荪，简明电路分析基础[M]，北京，高等教育出版社，2002

[4]陈洪亮等，电路分析基础[M]，北京，清华大学出版社，2009

[5]邱关源，电路(第四版)[M]，北京，高等教育出版社，1999

[6]于歆杰，电路原理[M]，北京，清华大学出版社，2007

[7]倪光正，工程电磁场原理(第二版)[M]，北京，高等教育出版社，2009

[8]Anant agarwal，于歆杰等译，模拟和数字电子电路基础[M]，北京，清华大学出版社，2008

[9]电磁场(电工原理II)[M]，北京，冯慈璋.，人民教育出版社，1979