关于大整数分解的方法探究

杨晨鹤　王周宁馨　张祯

摘 要：RSA是目前被广泛应用的公钥密码加密体制之一，其核心等同于大整数分解。文章对大整数分解问题提出新想法。分别就探索素数在二进制下的0与1的个数比例、平方整数分解方法、多项式分解方法三个方面，展开探究，给出可实现的算法，对每种方法的可行性进行分析，并结合简单例子，予以实践验证。研究0-1比例运用三次样条差值的拟合，说明了素数分布规律有一定的随机性；平方整数分解是费马经典算法的延伸，巧妙利用Lasvegas算法逼近分解所需的平方数；多项式分解方法则是将问题对应到一元高次多项式的分解问题上，其解决依赖于已有的多项式分解的理论。

关键词：大整数分解 平方整数分解 多项式分解 RSA

中图分类号：TP338.8 文献标识码：A 文章编号：1672-3791（2015）03（a）-0243-02

因子分解从其诞生到现在已有数百年的历史，然而真正引起数学家、密码学家及计算机科学家的极大关注却是近十几年的事，最直接的原因是因为一些新的密码体系及签名格式的安全性被认为是基于大整数因子分解的难解性。而对RSA中大整数的攻击有以下两个方面：（1）计算机革新，运算型攻击。量子计算机的诞生使RSA受到了一定的威胁；（2）算法的革新，从古老的费马算法到连分数攻击，二次筛因子法，以及椭圆曲线法，也逐渐有效地缩短了攻击RSA的时间。该文将立足于算法，对大整数分解提出一些新的思路，并解释几类容易被破解的大整数的原因。

1 二进制下的素数0与1比例探索

1.1 基本原理

这个思路来源于《素数分布——素数硬币的抛掷运动》这篇文章，分解一个大整数，需寻找其素因子（N=p×q）。这个过程是由一个已知数去寻找两个未知数，构成了较大的困难性。故从问题的反面考虑，通过运算、比较一定数量的已知素因子，寻找其乘法规律。下设两个素因子在十进制下分别有位与位，有位，即有如下的乘法关系式：

1.2 的性质

二进制下研究素数的分布的考察点是，先观察的性质。

1.2.1 有界性

，其中是一个关于的复杂函数，它与素分布有关。

1.2.2 存在性

每一个所对应的都是一个确定的数。

1.3 算法实现

：设置边界数T （T 不宜太大）。

：从0到T计算，计算到之间所有素数在二进制下1的个数，记为，及为其间0的个数，并用数组储存对应的比值，对应输出。

：绘制“”图像，并用MATLAB拟合。

：从数列中寻找收敛子列，并尝试找出其极限。

1.4 图像结果（测试T=24以内素数比值）

1.4.1 数据表（用C++编程测试）

舍去第一项无效的结果后，用MATLAB绘制图像，如图1所示。

1.4.2 图像

（1）未拟合图像；

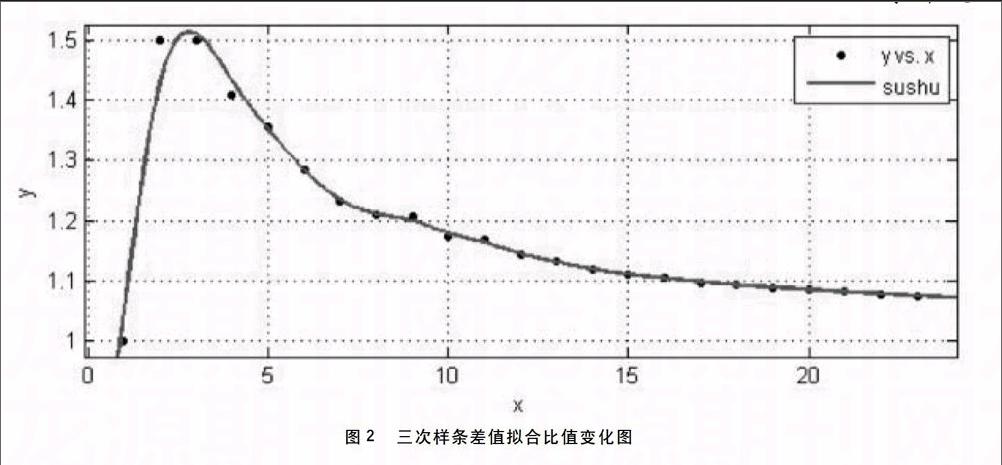
（2）三次样条差值拟合图像，如图2所示。

1.5 小结

比值在目前测试结果中，比值趋于1.05这表明二进制下素数1与0的比值研究可能会是比较困难的，说明了素数的分布有一定的随机性，但却提供了一种独特视角观察素数特征。

2 平方数法分解因式

2.1 基本原理

此方法基于“费马分解大整数”的方法，通过逐步改进平方数的寻找方法，使平方数的差值为待分解数，从而达到分解大整数的目的。

具体思路如下：令代分解的大整数为 ，假设其并非是完全平方数（在后续程序中第一步进行开根号运算，若得非整数结果才会继续下面的程序，从而避免算法寻找失败），那么它可以分解为两个素因子p，q 即，取整数满足下列关系式：

2.2 分解中S2与T2的存在性

若是完全平方数则可以通过第一步开根号运算结果进行判断；若是非完全平方整数，且只有两个素因子的情况下一定可以通过（2.1.1）来构造S2与T2，而（2.1.2）式又可以通过高斯求和方式遍历平方数，故上述算法是可实现的。

2.3 算法描述（算法）

：初始化求和存储变量，

：对给定的做初始判断，若为整数，则算法结束；若非，则进行。

：，若，则继续执行，否则执行。

：，若，则继续执行，否则执行。

：，若，则输出算法结束；若则原有执行；若，，执行。

3 结语

以上介绍了一种探索素数分布的思路和两种大整数分解在计算机下实现的算法。首先，探究的素数规律，通过计算素数在二进制下0-1个数比例，模拟图像，观察素数特征。其次，建立在费马算法上的平方整数分解方法，旨在用奇数和表示平方数，以遍历算法逼近用以表示所拆分大整数的平方数。最后，将大整数分解转移至已有较完备算法的多项式分解问题上。通过找寻多项式分解的因式，来突破整数分解的问题。而现在一定范围内的多项式分解是可以在计算机上实现分解的，从而说明了其有效性。

参考文献

[1] 曾泳泓.大整数因子分解算法综述[J].国防科技大学，1991（4）：21-32.

[2] 许小勇，钟太勇.三次样条插值函数的构造与Matlab实现[J].兵工自动化，2006，25（11）：76-78.

[3] 百度百科.拉斯维加斯算法.http：//baike.baidu.com/link.url=NwHY9 w5CTv9kGLBTld8Ln-wHLM6Yle5 usyS59Q3trDUC7DswnOf9EOLue 46NQXrS6P4UZshup0ZHQIRGfN-r_2014.12.5.