数学教学中培养学生推广能力的探讨

丁黎明,赵 冬

(淮北职业技术学院基础部, 安徽淮北235000)

数学教学中培养学生推广能力的探讨

丁黎明,赵 冬

(淮北职业技术学院基础部, 安徽淮北235000)

介绍数学推广的概念,分析数学推广在概念、公式及定理中的应用形式,结合具体的教学实例,根据数学内容从不同的角度提出数学推广的思想方法,探讨培养学生数学推广问题能力的途径,进而培养学生的创新精神。

数学推广; 应用类型; 思想方法; 数学创新

一、引言

数学推广是指在一定范围内或一定层次上对数学的概念、公式、定理、法则等进行拓展,使之在更大范围内或更高层次上成立,也指对条件、结论进行结构分析后,作适当变化,得到新的命题为真。推广是数学学习和研究的基本方法,也是人们发现数学规律的重要工具。在数学研究中,许多概念的建立都是通过推广现有概念而得到的,许多重要公式、定理和法则也是通过对已知命题的推广而被发现的。

对于数学教学的目的,仅要求学生掌握基本理论知识是远远不够的,要想让学生从数学学习中终生受益,就需要培养学生独立获取知识的能力,在教学中就要有意识地培养和发展学生的推广能力。随着人们对数学教育认识的不断深入,实现数学在培养学生提出问题、分析问题和探索解决问题的能力,在很大程度上取决于培养学生推广问题的能力。

二、在数学教学中贯穿各种应用类型的推广形式

数学的发展突飞猛进,数学的分支愈来愈多,数学的应用日益广泛,这些都是数学家们善于从生产实践和数学内部矛盾中不断地提出问题和推广问题,促进数学不断发展的结果。在数学教材中有很多概念、公式和定理都涉及到推广,并且有些推广公式或推广定理的使用甚至比原公式或原定理的使用更广泛。

(一)概念的推广

对于函数的概念,按照自变量的个数,只含有一个变量的称为一元函数;含有两个变量的称为二元函数;依次推广到含有n个(n≥3)变量的称为n元函数。再比如高阶导数的概念,函数的一次求导称为一阶导数;一阶导数的导数称为二阶导数;依次推广到(n≥3)阶导数的导数称为n阶导数。在概念中使用推广的方法直观、形象,便于学生理解掌握。

(二)公式的推广

(三)定理的推广

费马大定理是一个举世闻名的例子,毕达哥拉斯方程x2+y2=z2的整数解存在,在此基础上,法国的数学家费马将毕达哥拉斯方程中的2次幂推广到正整数n,当n≥3时,相应的方程xn+yn=zn有没有正整数解?以后的几百年来,吸引了许多优秀的数学家去研究并采用多种方法试图去证明这个定理。

后人也有这样的类似推广:x3+y3+z3=u3是否有整数解?xn+yn+zn=un是否有整数解?

x4+y4+z4+u4=v4是否有整数解?xn+yn+zn+un=vn是否有整数解?

以此类推,可见,数学家们总是不断地提出和推广问题,其中也会有解决不了的问题,从而推动着数学的向前发展。

三、数学推广问题的产生

(一)社会实践活动的产生

人们在生产和社会实践中,经常会面临各种各样的实际问题,对于这些实际问题中存在的数量关系和空间形式提取出来,进行深入分析研究,就会从中抽象出数学问题,进而推广问题。

(二)自然科学发展的刺激

自然科学与数学之间存在一种相互影响、彼此促进的亲密关系。一方面,数学为自然科学的发展提供定量描述、计算的工具;另一方面,自然科学则不断地向数学提出大量富有挑战性的问题,由于要解决自然科学提出的大量数学问题,进而促进数学自身的发展。

(三)数学内部自身的需要

数学发展有其相对的独立性,尤其是当一门数学分支学科形成理论体系之后,为求得自身体系的完善发展,它就开始不断地向自身提出各种各样新的问题,进而推广问题,激励着数学家们为丰富、完善该理论体系而不断作出创造。

四、培养学生数学推广问题能力的途径

在数学教学过程中培养学生推广问题的能力是必要的,也是可行的。结合学生的实际情况,对概念、公式、定理和问题应当从不同的角度和方向引导学生学习和适当进行推广,这对激发学生的创新精神、培养学生的创造能力会有很大帮助。

(一)用推广问题学习新知识

两个函数积的求导法则:两个可导函数乘积的导数等于第一个因子的导数与第二个因子的乘积,加上第一个因子与第二个因子的导数的乘积。

引理[1-2]:如果函数u=u(x)和v=v(x)在点x处都可导,则函数f(x)=u(x)v(x)在点x处可导,且fˊ(x)=uˊ(x)v(x)+u(x)vˊ(x),简记为(uv)ˊ=uˊv+uvˊ。

对于积的求导法则也可以推广到任意有限个函数之积的情形。例如,三个函数乘积的导数(uvw)ˊ=uˊvw+uvˊw+uvwˊ,四个函数乘积的导数(uvwh)ˊ=uˊvwh+uvˊwh+uvwˊh+ uvwhˊ,依次推广n个函数乘积的导数(x1x2…xn)ˊ=x1ˊx2…xn+x1x2ˊ…xn+…x1x2xnˊ,于是可得n个函数积的求导法则:n个可导函数乘积的导数等于第一个因子的导数与其余n-1个因子的乘积,加上第二个因子的导数与其余n-1个因子的乘积,依次加上第n个因子的导数与其余n-1个因子的乘积(含n项乘积之和)。

(二)用推广问题探究数学规律

闭区间[a,b]上的连续函数f(x)一定存在最大值和最小值,即引理[1-2]:若函数f(x)在区间[a,b]上连续,则函数f(x)在[a,b]一定存在最大值和最小值。

在教学中可以这样推广问题,启发学生,探究数学规律:当函数f(x)在半开区间[a,b)或(a,b]上连续,则函数f(x)的最大值和最小值是否存在?

当函数f(x)在开区间(a,b)上连续,则函数f(x)的最大值和最小值是否存在?

推广1:若函数f(x)在半开区间[a,b)上连续,且在(a,b)内fˊ(x)＞0(或fˊ(x)＜0),则函数f(x)在[a,b)上一定有最小值(或最大值)。

证明:由于在(a,b)内fˊ(x)＞0,则函数f(x)在[a,b)上单调增加,不妨设f(a)=A,从而对∀x∈(a,b),都有f(x)＞f(a)=A。因此,函数f(x)在[a,b)上一定有最小值。

同理可证:函数f(x)在半开区间[a,b)上连续,且在(a,b)内fˊ(x)＜0,则函数f(x)在[a,b)上一定有最大值。

推广2:若函数f(x)在半开区间(a,b]上连续,且在(a,b)内fˊ(x)＞0(或fˊ(x)＜0),则函数f(x)在(a,b]上一定有最大值(或最小值)。证明:同推广1。

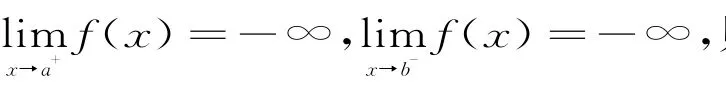
(三)用推广问题帮助解题

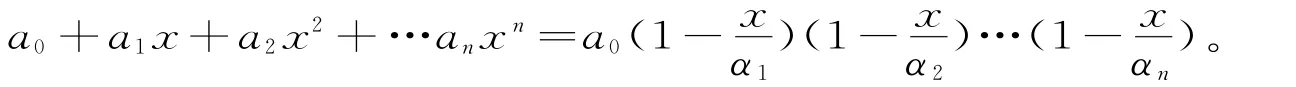
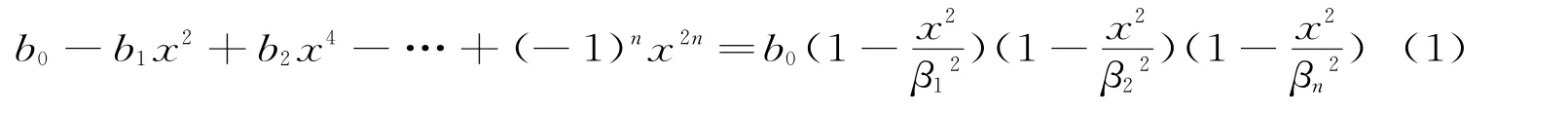
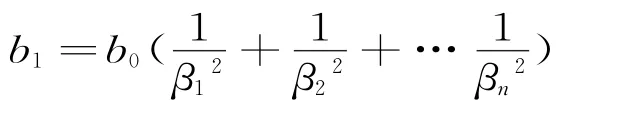
五、结论

数学推广是高校数学教学不可缺少的重要内容之一,也是高校教师综合教学能力的体现.在高校数学教学中,用数学推广的思想方法启发学生去大胆探索,培养学生独立思考、勇于创新的科学精神,培养学生初步掌握数学推广问题的研究能力,是高校数学教师义不容辞的责任。

[1] 同济大学数学教研室.高等数学(上册):第4版[M].北京:高等教育出版社,1996.

[2] 华东师范大学数学系.数学分析(上册):第2版[M].北京:高等教育出版社,1998.

[3] 朱彩兰.关于开区间内连续连续函数最值的判定[J].高等数学研究,2010(5):43.

[4] 顾泠沅,朱成杰.数学思想方法[M].北京:中央广播电视大学出版社,2004.

On Cultivation of the Generalization Ability for Students in Mathematics Teaching

DING Li-ming,ZHAO Dong
(Department of Basic Courses of Huaibei Professional&Technical College, Huaibei Anhui 235000)

This paper introduces the concept of mathematics generalization,analyzes the application of mathematics generalization in concept,formula and theorem,combined with specific examples of teaching, and then puts forward the idea of mathematics generalization from a different point of view according to the mathematical content.Finally it explores the ways of cultivating the ability for students of mathematics generalization problems,which can cultivate the innovation spirit for students.

Maths generalization; application type; thought methods; Maths innovation

G712;O13

A

1671-4733(2015)01-0084-04

10.3969/j.issn.1671-4733.2015.01.025

文献类型和标志代码

文献类型电子公告标志代码普通图书会议录汇编报纸期刊学位论文报告标准专利数据库计算机程序M C G N J D R S P DB CP EB

2015-02-26

丁黎明(1969-),女,安徽淮北人,硕士,副教授,从事高等数学教育教学工作,电话:0561-3111473。