基于高职环境下微积分教学内容的研究

徐利民,梅灿华,白 灏

(淮南职业技术学院基础部, 安徽淮南232001)

基于高职环境下微积分教学内容的研究

徐利民,梅灿华,白 灏

(淮南职业技术学院基础部, 安徽淮南232001)

“质量没有最好的,只有最适应的”,在高等职业教育环境下微积分教学内容应该与学生的数学基础相适应,应该与实际课时资源相适应,应该与实际真实应用相适应;通俗,直观易懂,简易明快,使学习者能在较短的时间里明白其原理是第三代《微积分》发展的方向;通过对几点教学内容和现状进行分析和研究,探讨了高职微积分教学内容的思想与应用的适应性,以及极限理论直观教学的适应性。

高职教育; 微积分; 教学内容; 适应性

一、现状分析

高等职业教育是一种普及型的高等教育,国家在2010-2020年中长期教育改革和发展规划纲要指出:“职业教育要面向人人、面向社会,着力培养学生的职业道德、职业技能和就业创业能力”,要“改革招生和教学模式”。进一步明确了职业教育的发展方向与培养目标。近年来,高等职业教育的办学规模有了很大的发展,同时高等职业教育的教学质量也普遍备受人们关注。在高等职业教育的环境下,怎样提高数学的教学质量,实现数学应有的价值,面对高等职教育招生制度改革的构想与实施,高职数学教学面临更多的考验。改变教学思路,构建适应的数学教学内容,才能适应新的教学环境。现阶段高职《高等数学》课程,主要讲解《一元微积分学》的内容。实际教学过程中,数学教学质量受到许多因素的影响。

在落实高等职业教育的教学思想,提高学生的职业能力和知识的应用能力,加强实践环节的教学。各专业课程的教学内容也已降低了对数学的要求,数学课程的教学时数也作了相应的调整下降。数学教学任务重与课时资源紧缺的问题突出。

由于扩招高职学生的入校门槛降低(近年来呈现逐年下降的趋势),学生的数学基础对数学教学有很大的影响。学生的数学演算能力与数学分析能力也阻碍了数学教学进程和学生课后作业的独立完成。数学教学的效率不高。

调研表明专业课程的学习对数学的演算能力的要求不高,实践就业环境也很少“用到”,课程又难学,学了也难以用得上。另外一方面,作业完成情况是传统的学习考核与学生自我评价的主要方式,这都大大影响许多学生学习的兴趣和积极性。这样期望通过课后练习来深化理解概念和定理等教学内容的教学方式,不能获得实际满意的教学效果。所以高等职业教育数学教学的效率不高作用不大问题更为突出。

经历了多年高等职业教育数学教学内容的改革,精简了教学内容,按要求略去繁琐的推导过程,降低了作业难度和学习要求,但还有许多地方存在着不足。以做题来衡量评价学生学习的考核方式没有改变。

按照现代质量观“质量没有最好的,只有更适合的”[1]。在高等职业教育环境下,必须发挥教师的引导作用,加强教学内容和教学方法的研究,增加教学内容与教学方法的适应性。教学内容“通俗,直观易懂,简易明快,使学习者能在较短的时间里明白其原理”是第三代《微积分》发展的方向[2]。实际真实有用,有利于提高学生的学习能力和实际职业能力是职业教育对数学的要求。

二、微积分教学内容的研究

(一)微积分教学的基本任务

从职业教育专业建设的角度来说,微积分教学的基本任务应服务于专业建设,有利于提高学生对专业课程的学习和理解能力,有利于实践中提高学生的职业能力。从数学教学的角度来说,在高等职业教育数学教学中,在具体的条件下,微积分教学怎样更好地服务于专业建设。在微积分教学内容中,除包含微积分的基本原理,还包含着近代数学思想和科学方法。

代数与微分几何学家格列夫斯指出“刚起步的学生需要知道比事实和技巧更多的东西:吸收一种数学的世界观,一种判断问题是否有意义的准则,一种向别人传递数学知识、数学热情和数学味道的方法”[3]。近代科学方法论的奠基人伽利略(Galileo)倡导用“量的公理”和数学演绎的方法来研究自然科学[4]。

如科学家们选择一个基准的长度单位(如米、公里、尺、丈等)来衡量距离的远近和物体的长短,选择一个基准的单位面积单位(如平方米、平方公里、亩等)来衡量区域面积的大小一样。现代经济学家用“弹性”来表示销售量对价格反应强度。系统工程学家用在规定时间内系统设备能够正常工作的概率来衡量系统设备的可靠性(即在规定的时间内设备能正常工作的能力)等。有了公认合理量的定义,通过数学演绎和推理分析,获得一些有用的结论。由伽利略(Galileo)创建,牛顿(Newton)继承的科学工作方法,“将基本的物理原理表示为定量的数学陈述后,利用数学的论证,推出新的成果”。同样在一元微积分学中,从速度概念与面积等概念出发,用极限的方法,通过分析推理,建立了微积分两大基本概念(导数与积分)理论,解决了近代“四大科学问题”,同时“四大科学问题”促进了微积分学的创立与发展[4]。数学的进步使得一些科学问题得到了解决,科学的方法论也促使数学与其它学科内容和方法思想的融合。学习微积分的基本原理,培养学生对微分(导数)和积分概念理论的理解,传递一种科学方法,增加一份数学的情感,培养使用数学的世界观和方法来理解问题与分析问题,促进提高学生的学习能力和职业能力。

(二)微积分教学内容的应用性分析

现代高职教学越来越重视应用的教学,对数学理论教学的效用的质疑是显然的。教育部等六部门在《现代职业教育体系建设规划(2014-2020年)》(教发[2014]6号)文件中指出,“职业院校按照真实环境真学真做掌握真本领的要求开展教学活动”。近代数学发展的历史也表明,“数学工作的主要目的不是数学,是达到科学研究目的一种方法”[4],是解决实际问题的一种手段。近代数学家极少有对其他科学不感兴趣的,“欧拉(Euler)研究过帆船设计和弹道学。蒙日(Monge)研究过风车的枫叶设计,特别是“物理学、力学是数学的福地”。“将基本的物理原理表示为定量的数学陈述后,利用数学的论证,推出新的成果”。数学不仅需要这些成果来证明数学发展方向的正确性,有时同样也需要物理实验的结果来证明数学的可靠性。微积分教学内容中包含有大量应用实例体现了数学教学内容的实用性。

在高等职业教育中,数学教学的价值需要在专业教学与实践中得到体现,数学教学内容应当更多的关注专业建设方向,能够有更适应的具体的教学实例,才能更好地适应高职学而知其用的要求。深刻理解“够用为度”的教学原则,在有限的教学时间内,根据学生的数学基础,实现这一原则,有利于帮助提高学生的“职业技能和就业创业能力”等,以此来确定数学教学内容选择的正确性。

(三)微积分内容教学难点分析

“第一代微积分是说不清楚的微积分。第二代微积分是严谨的,说得清楚的,听不明白的微积分”[2]。

当人们以运动的观点来研究变量与变量之间关系的时候,也就预示着数学新时期的到来。由牛顿(Newton)和莱布尼兹(Leibniz)创立的《微积分》,称为第一代微积分[4]。当人们观察在自变量x→x0(或x→∞)的条件下,函数f(x)的变化趋势时,那时科学家很清楚自己想做什么,但却很难清楚地用日常通俗的语言来表达,因为他们期望观察到的那个距x0“最近”而又不等于x0的点根本就不存在;其二极限值的判断是主观的,极限值判断的正确与否依赖于直观的、几何的等方法的选择、以及以往的知识积累。自然在逻辑上是不严格的,因此“这一时期的微积分的概念是模糊的,说不清楚的”。牛顿试图改变这一切,建立一个不需要极限概念的微积分,但没有成功[2],莱布尼兹并不担心这些,他更多关心是由此所获得的那些有用的结论。直到19世纪中叶(1859年),维尔斯托拉斯(Weierstrass)改进了柯西(Cauchy)等人的工作,公布了一个严谨的极限定义[4],其后人们对所判断极限值有了一个确定其正确性的准则,即所判断的极限值A,如果满足由维尔斯托拉斯所给出的定义,则所判断的极限值是正确的,否则所判断的极限值是不正确的。由此建立的微积分学,称为第二代微积分。“第二代微积分是严谨的,说得清楚的”,但极限概念定义过于抽象推,理繁琐迂回,“使绝大多数学习微积分的学生听不明白”[2]。

在高等职业教育中,面对《微积分》教学所遇到的困难,促使微积分教学放弃逻辑上的严谨性。极限教学只讲极限认知的第一步,即极限值的判断,略去了繁琐的“ε-δ”语言的证明。鉴于学生的数学基础和教学课时资源的紧缺,为了增加学生的理解和提高学习的反应速度,选择研究直观的教学方法以增加教学的适应性。

(四)极限概念直观几何表述的探讨

在高等职业教育中,由于受到学生的数学基础和教学时数的影响,极限理论教学所遇到的困难更加突出,必须选择相适应的策略和教学方法,有利于保证实际教学效果的提高。虽然初等函数的连续性在高等数学的教学内容中才能有更好的理解,但充分利用学生在初等数学学习中对基本初等函数图像已经建立的认识,开展极限理论的直观教学是有利的。

在由维尔斯托拉斯给出的严格的极限定义(任给(可以任意小的正数)ε＞0,存在δ＞0,只要0＜|x-x0|,就有|f(x)-A|＜ε。)中,0＜|x-x0|＜δ表示x0点处近旁的点。由于ε是可以任意小的正数,所以|f(x)-A|＜ε表示函数值f(x)集中在“A点处”。即当x→x0时f(x)→A,在几何上,可以通俗的理解为函数f(x)在x0近旁点的函数值都集中“A点处”。

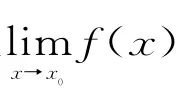
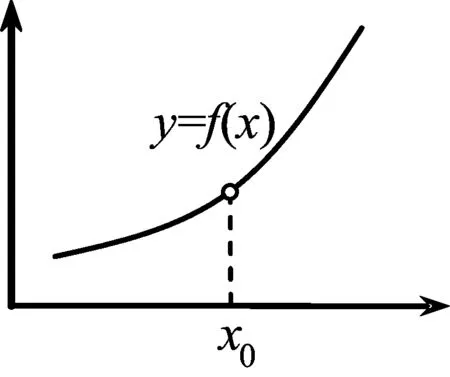
图1 函数示图

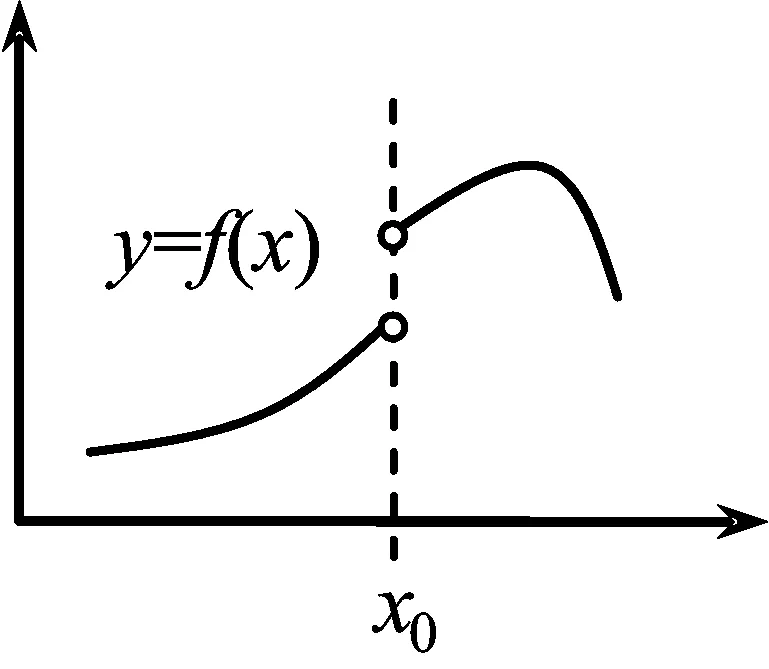
图2 函数示图

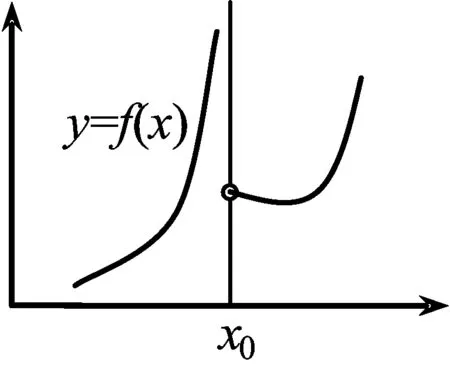
图3 函数示图

三、结束语

“数学工作的主要目的不是数学,是达到科学研究目的一种方法”,是解决实际问题的一个手段。只是在微积分严谨性的发展过程中,才从纯数学的角度来研究微积分,研究和提出各种各样的纯数学问题,建立准确的概念,严密的逻辑基础和理论,使得数学越来越抽象。相对整个理论体系的可靠性来说,应用更具体地体现在相关专业课程的论述中。在高等职业教育教学中,鉴于学生的数学基础,教学课时资源的制约,教师的引导作用就显得特别的重要。适应的教学内容和教学方法需要认真地研究和把握,从专业课程中和专业实际工作环境中探索数学真实的应用,模拟真实环境的数学问题,才能为技术技能型人才的培养、学生的专业课程的学习和真实应用建立更适应的数学基础。

[1] 刘振天.没有最好只有更适合[N].中国教育报,2012-05-28(8).

[2] 张景中,冯勇.第三代的微积分[J].自然杂志,2010,32(2):67-71.

[3] 天津中德职业技术学院数学教研室.高等数学简明教程[M].北京:机械工业出版社,2003.

[4] M.克莱因.古今数学思想[M].上海:上海科技出版社出版,1979.

Research on Teaching Contents of Calculus in Higher Occupational Education Environment

XU Li-min,MEI Can-hua,BAI Hao
(Department of Basic Courses of Huainan Vocational&Technical College,Huainan Anhui 232001)

“Quality does not have the best,have only more suitable”.In the higher occupation education environment,the calculus teaching contents should be adapted to the mathematical basis of students, the actual resources of teaching and application.In the literature,“popular,intuitive,simple and lively, so that learners can in a relatively short period of time to understand the principle”is the direction of development on the third generation of calculus.In this paper,through the research on the teaching content of calculus and the analysis on the present situation of teaching,the adaptability of thought and application of the teaching contents and the adaptability of visual teaching of limit theory have been discussed.

higher occupational education; calculus; teaching content; adaptability

G712;O175

A

1671-4733(2015)01-0080-04

10.3969/j.issn.1671-4733.2015.01.024

2014-12-17

安徽省高等教育振兴计划项目(项目编号:2014ZDJY156);安徽省高等学校质量工程研究项目(项目编号:2013gxk118);淮南职业技术学院教学研究项目(项目编号:HJX14-1).

徐利民(1961-),男,江苏宜兴人,副教授,从事教学研究工作,电话:0554-6656025。