玻璃钢定向器老化性能及蠕变行为研究

苏腾腾，于存贵，宋 涛

(南京理工大学机械工程学院，南京 210094)

为了适应现代战争突发性、速决性、机动性和灵活性等要求，必须将武器轻量化作为一个重要研究方向，采用非金属复合材料是实现轻量化的重要途径之一，玻璃钢逐步取代传统金属成为定向器用材料的首要选择［1-2］。在长期的贮存中，玻璃钢的老化性能对定向器可靠性和寿命有很大的影响。

为了保证玻璃钢定向器贮存的安全可靠性，本文深入研究定向器用玻璃钢材料的老化性能及蠕变行为，并提出相应的蠕变估算方案，为非金属定向器的贮存可靠性及寿命预测研究提供一种思路。

1 玻璃钢定向管老化性能研究现状

1.1 玻璃钢定向器仓库贮存环境

定向器是火箭炮储运发射箱的重要组成部分，对火箭弹的贮存可靠性、安全性有重要的保障作用［3］，贮存环境对玻璃钢定向器的寿命有很大影响，采取一些措施保障库房环境标准，如控制温湿度在一个合理的范围内是保证定向器贮存寿命指标的重要手段。

弹药的贮存库房环境条件相对其他军用物资更为严格，定向器的贮存环境标准应从延长弹药的保管年限，保持弹药的良好状态出发，根据军用物资贮存环境要求，弹药贮存的温度应该控制在5 ～20℃范围内，相对湿度应控制在55% ～65%范围内［4］。

1.2 研究方法

诸多外界因素的联合作用使复合材料产生老化，裂纹由表层慢慢深入内部，进而破坏复合材料的基体、增强体与界面之间的关系，从而引发材料性能的变化。玻璃钢老化一方面受到环境等外界因素的影响，也与所选用的纤维、树脂种类和成型工艺等有关［5］。目前广泛使用的老化研究方法主要分为自然老化和加速试验老化。

自然老化是将典型的制品或使用条件作为对象进行系统的研究，典型的使用条件有大气曝晒、库存、加热、水浸泡和化学侵蚀。加速试验主要以人工气候试验、湿热试验和煮沸等为手段。

1.3 研究现状

随着火箭武器轻量化发展，玻璃钢被广泛应用于军工产品，定向器用玻璃钢采用环氧树脂和辅料为基体材料，以玻璃纤维及其织物为增强材料复合而成，制造时一般采用玻纤缠绕工艺。

根据《玻璃钢的耐候性》中关于定向器用玻璃钢材料的老化试验数据，环氧树脂玻璃钢在室内存放八年的弯曲强度保留率大于80%，大气曝晒三年后的弯曲强度保留率大于95%，玻璃钢作为定向器用材料，其耐老化性能满足长期贮存的要求。

对某玻璃钢弹药包装筒进行露天恶劣条件的实弹包装贮存试验，考察其长期贮存的可靠性，试验表明，贮存15 a 后弹药各项指标均满足发射爆炸需要，所以玻璃钢定向器能够作为火箭弹包装筒进行长期贮存，并具有很好的可靠性［6］。

2 玻璃钢定向器的蠕变行为

2.1 蠕变机理

为了预测玻璃钢定向器长期贮存后的使用可靠性，要研究长期恒定应力条件下，玻璃钢定向器的蠕变变形。从材料角度来看，玻璃钢的蠕变性能除了与温度有关，还与其组成材料、组成比、成型工艺等因素有关。大量研究表明玻璃纤维的蠕变变形很小，Pearson 用玻璃棒进行1 000 h 的蠕变试验，蠕变量是弹性应变的0.2%［7］，玻璃钢的蠕变性能主要与树脂相关，在长期静载作用下，树脂分子沿力场方向重新组合排列，原本卷曲的分子伸直直到拉断，宏观表现为材料发生蠕变变形。

对玻璃钢定向器进行蠕变变形预测，结合定向器在直线度、圆度方面的形位误差要求，可判断玻璃钢定向器贮存寿命周期内任意时间段的使用性能和可靠性。

图1 为复合材料的蠕变曲线，与金属材料类似，蠕变大致可划分为早期蠕变阶段、稳态蠕变阶段和加速蠕变阶段。早期蠕变阶段蠕变速率随时间增长不断下降，稳态阶段蠕变速率最小且基本保持不变，持续时间最长，加速阶段速率突然加快，最终导致断裂。

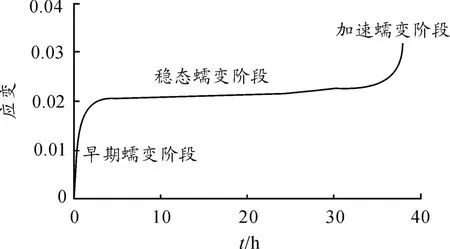
图1 复合材料蠕变曲线

2.2 蠕变模型

蠕变模型大概可分为经验形式、元件组合形式、积分形式3 种。经验形式模型是用数理统计方法对试验数据进行分析拟合验证而得到，但是一般只能描述蠕变前两个阶段，不能表示加速蠕变阶段。最能反映材料蠕变性能的是元件组合形式，它是由理想弹性元件和粘性元件组合而成，例如比较著名的三元素模型、Maxwell 模型、Kelvin 模型等。积分形式用于外力不是常数时，材料应力、应变和时间之间的关系。

2.2.1 Schapery 蠕变理论［8］

由于多数聚合物仅在较低应力和较低温度下呈现线性黏弹行为，Schapery 蠕变理论克服Boltzman 模型局限，从不可逆过程热力学熵增加原理和自由能概念出发，建立等温单向应力条件下非线性黏弹性本构方程［9］

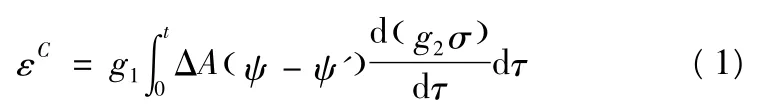
设材料蠕变服从幂律:

由式(1)、式(2)可以得出:

g1、g2是与应力有关的材料参数;ΔA(ψ)为蠕变柔度的函数;ψ、ψ'是折算时间;为了便于分析，取σ 为常数;C、n 为材料常数;K'σ是与应力相关的材料参数。

2.2.2 Rabotnov 蠕变理论［10］

在早期蠕变阶段，变形主要是剪切屈服，基体中的纤维诱发细小的裂纹，形成损伤，到蠕变中后期裂纹对蠕变变形起主导作用［11］，本研究基于Kachanov-Rabotnov 理论，建立定向器用玻璃钢材料的蠕变模型。Rabotnov 蠕变理论公式如下:

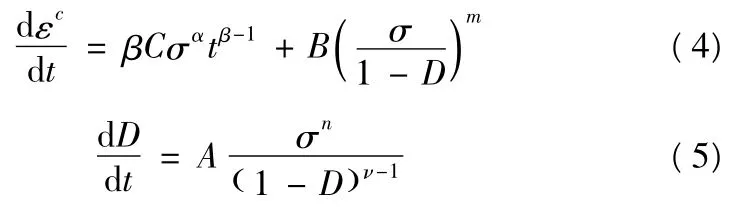
式(4)中:D 为损伤变量;D =0 时材料无损;D =1 时材料破坏;A≥0，n≥1 为材料常数。

当初始条件t=0，D =0;断裂时t =tf，D =1，对式(5)进行积分得:

将初始条件t=0，εc=0，将式(6)代入式(4)积分得:

式(7)中前一项代表剪切屈服对蠕变变形的贡献，后一项表示裂纹扩张引起的损伤对蠕变的贡献。

蠕变的初始阶段，剪切屈服占主要作用，可得蠕变变形为

蠕变的稳态阶段，损伤量很小，可认为D=0，代入式(4)积分可得

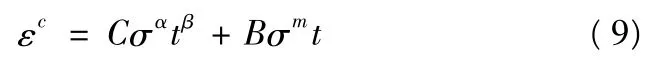
蠕变断裂时t=tf，εc=εf，代入式(7)得:

3 蠕变估算试验

3.1 试验方案及结果

取玻璃钢定向器最薄处厚度作为工字型试样的厚度，采用E 玻纤作为增强材料，双酚A 型环氧树脂作为基体的玻璃钢试样，在牵引机的作用，进行1 000 h 的拉伸蠕变试验，试验温度为常温。

为了消除试样加工中的残余应力，保证试验过程中工作区域的有效变形和破坏，在试验前对试样进行加载，载荷为蠕变应力的90%，再进行卸载，重复10 次，保证试验数据的可靠性。试验过程中试样断裂时，试验即终止。分别对3 种不同应力水平下的试样进行测量，试验数据如表1。

表1 玻璃钢蠕变变形量

3.2 试验结果评判

将所得的试验数据在计算机中进行线性拟合，得到图2所示的曲线。在计算机中将Schapery 蠕变理论模型和Rabotnov 蠕变理论模型中的未知参数进行回代验证，得到两种模型中玻璃钢材料的相关参数，由数学模型函数关系可知两种模型对于玻璃钢材料蠕变的初始阶段和稳态阶段的描述很好，但是Rabotnov 蠕变理论模型对于中后阶段的蠕变描述则更为合适，Schapery 蠕变理论模型则中后期趋于平缓，不能描述加速阶段蠕变速率突然增大直至材料失效，如图3所示。

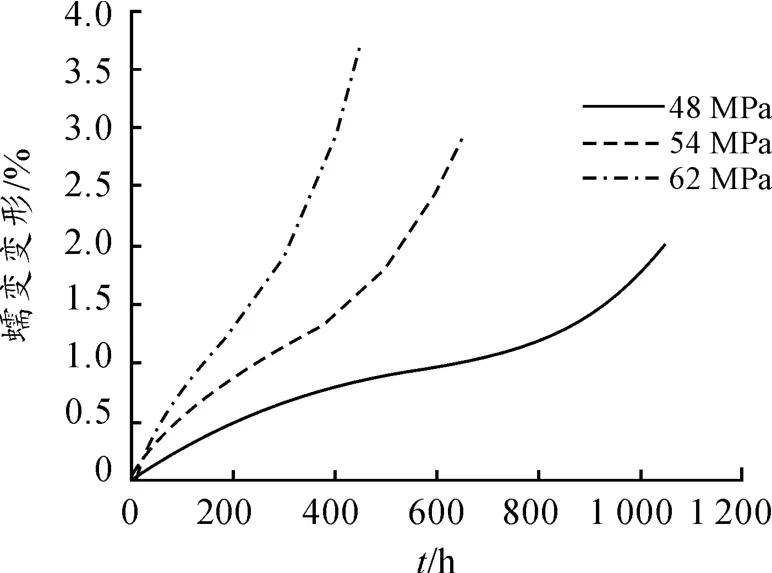
图2 蠕变变形试验拟合曲线

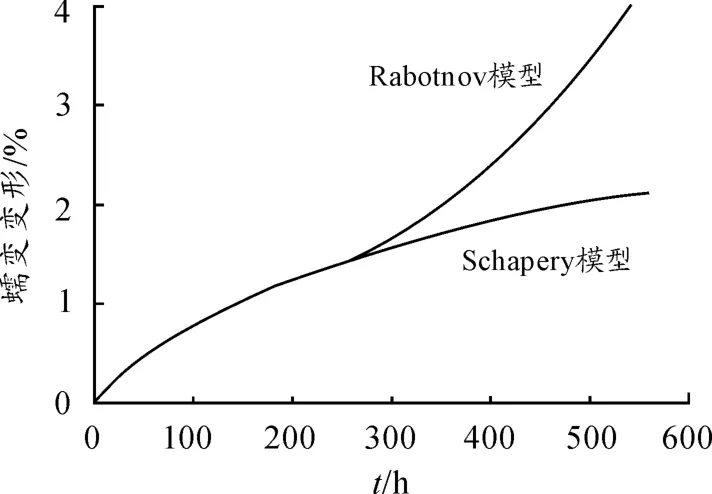
图3 Schapery、Rabotnov 模型蠕变变形对比

4 结论

目前，复合材料蠕变试验研究明显领先与理论研究，而且树脂基复合材料蠕变性能研究还没有形成系统。一方面由于复合材料的种类繁多，另一方面由于影响因素较多，对于常见的工程用树脂基复合材料的蠕变性能也没有定量的研究结论。

本文从复合材料本构关系研究，希望为深入研究复合材料蠕变模型、控制设计材料的蠕变提供理论基础。希望可以结合有限元仿真软件，通过二次开发等方式，将玻璃钢定向器的蠕变本构模型写入程序，通过仿真，预测玻璃钢定向器在一定贮存寿命周期内的蠕变变形。

［1］李培珍，李志刚.复合材料定向管力学特性仿真［J］.兵工学报，2012(11):1404-1408.

［2］张中利，党玉功，乐贵高，等.玻璃钢定向器热弹性能数值仿真与分析［J］.系统仿真学报，2010(4):77-880.

［3］王轲，张福祥.玻璃钢制火箭炮定向器的强度研究［J］.弹道学报，2003(2):39-43.

［4］GJB 2770—1996，军用物资贮存环境条件［S］.

［5］Jun Koyanagi，Genyakiyota，Takashi Kaniya and Hiroyuki Kawada.Prediction of creep rupture in unidirectional composite Creep rupture model with interfacial debonding and its propagation［J］.Composite Mater，2004(13):199-213.

［6］赵锡鑫，王海明，朱志敏.某新型非金属定向管老化性能测试及寿命估算方案研究［J］. 火炮发射与控制学报，2013(2):55-58.

［7］周祝林，杨云娣. 纤维增强塑料蠕变机理的初步探讨［J］.玻璃钢/复合材料，1985(8):29-33.

［8］Schapery R A.Workshop on a continuum approach to damage and life prediction ［J］. National Science Federation，1980:119-133.

［9］Papanicolaou G C，Xepapadaki A G，Pavlopoulou S，et al.On the investigation of the stress threshold from linear to nonlinear viscoelastic behaviour of polymer-matrix particulate composites［J］.Mech Time-Depend Mater，2009(13):261-274.

［10］Rabotnov Yu M. Creep problems in structural members.Amsterdam:North-Holland，1969.

［11］樊建平，彭立华，沈为.正交玻璃布/环氧复合材料蠕变损伤试验研究［J］.复合材料学报，1995，12(4):84-88.