某火箭炮闭锁机构工作性能分析
武秋生,马大为,肖 雄
(南京理工大学机械工程学院,南京 210094)
闭锁机构的作用是在发射前将火箭弹固定在定向器内,保证火箭弹在行军时和准备发射阶段在定向器内相对位置不发生改变,当发射时推力产生,能够为火箭弹提供统一的闭锁力。实践证明,稳定的闭锁力对提高射击密集度有帮助作用,其道理在于使一组火箭弹具备较一致的离轨速度,可以减少由于离轨速度散差造成的落点角偏差[1]。
本文针对某火箭炮改进型闭锁机构,为了研究其工作性能,对该闭锁机构的闭锁力大小进行了测试。由于实际发射时,定向钮与闭锁机构之间是一个高速冲击的非线性动力学过程,所以该测试结果只能作为参考值,并不能代表在实际发射工况下定向钮所受约束力的大小。然而实际发射试验存在着耗资大,准备周期长,环境复杂,数据难以采集等诸多弊端。随着有限元技术的发展,可以利用计算机和有限元软件对闭锁器进行瞬态动力学的研究。基于此,本文建立闭锁机构的有限元模型,研究了该闭锁机构发射条件下的工作性能。
由于闭锁机构的闭锁力在发射过程中是不断变化的力,因此它的取值有争议。陈四春等[2]提到将定向钮稳定运动且速度达到火箭弹设计初速1%时的推力值作为闭锁力,姜勇等[3]则认为应将定向钮所受约束力跳动之前的稳定值作为有效闭锁力。在传统的闭锁力解析式中,闭锁力随卡簧挠度的变化而变化,当挠度为零时,闭锁力最大,将其定义为闭锁器的最大闭锁力,并作为设计闭锁机构的主要参数。本文通过对发射条件下定向钮与闭锁机构之间相互作用历程的分析,认为应将定向钮所受最大约束力作为闭锁机构的闭锁力。
1 闭锁机构结构
卡簧式闭锁机构由卡簧和螺栓组成,如图1 所示。图1上面的闭锁机构为初始设计,闭锁器为改进型。初始闭锁结构的设计缺陷在于过度依赖于传统的解析式[4]。由于该闭锁机构的螺栓与传统闭锁器相比缺少球形部,使得卡簧变形集中在右半侧,所以在初始设计时闭锁器的闭锁力被高估,使得实际的闭锁力达不到设计值(设计值为1.8 ×104±500 N),而且其抵抗破坏的能力也比较弱。经过对虚线圈所示部位进行加厚设计,单片卡簧的厚度由14 mm增加到18 mm,得到改进型的闭锁机构。
闭锁机构工作时左端被固定在定位环内,右端锁住定向钮。点火后,当火箭弹推力大于闭锁力时,闭锁机构右端将被迫张开,完成发射过程。

图1 闭锁器结构示意图
2 闭锁机构闭锁力试验
文献[1 -2]均表明在一定范围内,闭锁机构的闭锁力随着预紧力的增大而增大,因此要获得较稳定的闭锁力,就必须对闭锁机构预紧力进行控制。以往控制闭锁机构预紧力的方法是将螺栓上螺母的旋进量(即卡簧的预紧挠度)作为控制量。本文利用测力扳手或定扭矩扳手来控制螺母的拧紧力矩,能够更精确的控制闭锁机构的预紧力。
测试试验所用仪器为日本岛津材料试验机,型号为AG-100KNI M2,测试装置如图2 所示。试验中用直径12 mm圆棒代替定向钮,通过定扭矩扳手为闭锁机构试样施加不同的预紧力。通过缓慢加载,测试闭锁机构在不同拧紧力矩下闭锁力的大小。

图2 测试装置
部分测试结果如表1 所示。通过表1 中测试结果可以得出以下结论:
1)将测试编号1 -2 的闭锁力数据与设计值(1.8 ×104±500 N)对比,表明改进型的闭锁机构在适当的预紧力条件下,闭锁力的大小可以满足设计值。
2)通过对比不同拧紧力矩条件下的闭锁力的数值,表明在试验范围内,拧紧力矩每增加5 N·m,闭锁力大约增大1 000 N。
3)通过对比相同拧紧力矩时的闭锁力数值,可以发现当闭锁机构被施加同一拧紧力矩时,其闭锁力的值比较稳定,说明本文提出的预紧力施加方法是可靠的。

表1 闭锁机构的闭锁力试验结果
3 有限元动力学分析
为了研究闭锁机构在发射条件下的工作性能,采用有限元动力学的方法建立闭锁机构的有限元模型,通过仿真计算,可以得到定向钮与闭锁机构之间的作用历程。
3.1 有限元模型的搭建
在SolidWorks 中建立闭锁机构的三维几何模型,通过中间格式导入有限元软件ABAQUS,将各个部件用减缩积分六面体单元(C3D8R)划分网格后,如图3 所示。根据所用材料将其弹性模量定为206 GPa,泊松比为0.3,定向钮与闭锁机构之间摩擦系数设为0.15。

图3 闭锁器有限元模型
分析步定义:动力学计算分两步进行,第1 步在通用分析模块Abaqus/Standard 中加载预紧力,第2 步在显示动力学分析模块Abaqus/Explicit 模块中进行,把第一步的计算结果作为初始状态导入,然后加载火箭弹推力,进行显示动力学分析。
火箭弹发动机推力的施加:根据火箭弹推力曲线和闭锁力可知,火箭弹的稳定推力值远远超过闭锁力,因此闭锁机构工作在火箭弹推力上升阶段(点火后30 ms),所以只需在定向钮上施加发动机点火后推力上升段的推力即可,该推力值从点火开始到第30 ms 均匀增加到248 000 N。
为便于分析,闭锁机构的有限元模型基于以下假设:
1)定向钮和定位环都定义为刚体,定位环与大地固连。
2)将火箭弹简化为定向钮上附加点质量。
3)定向钮所受推力沿X 轴方向,不考虑推力偏心的影响。
闭锁机构的预紧力是通过定扭矩扳手施加的,在模型中,由于螺栓已经简化,拧紧力矩M 的施加并不可行,可以通过施加螺栓载荷F(Bolt Load)来代替。拧紧力矩M 与螺栓载荷F 之间的关系[5]为

式(1)中:D 为螺纹公称直径(mm);F 为预紧力(N); K 为阻力系数闭锁器所用螺栓直径12 mm,阻力系数取0.2。从第2小节结论1)可知在施加6 N·m 拧紧力矩时,闭锁力已经达到设计指标,因此仅仿真闭锁机构不加拧紧力矩和拧紧力矩为6 N·m 两种情况。
3.2 计算结果分析
针对两种预紧力情况下的有限元动力学计算结果如表2所示。

表2 不同预紧力下的计算结果
通过对比表2 中的闭锁力与第1 小节中的试验得到的闭锁力,可以得到以下结论:
1)试验条件下测得的闭锁力数值与有限元计算的闭锁力的数值有很大差别。表明试验数据可以作为闭锁器闭锁能力的参考,但是不能代表发射时闭锁机构与定向钮之间复杂的相互作用力。
2)不同预紧力下火箭弹挣脱闭锁机构时的速度是不同的。确定闭锁机构闭锁力设计值时应考虑到其对火箭弹离轨速度的影响。
定向钮与卡簧之间的接触力包括摩擦力和接触压力产生的反作用力两部分。闭锁机构的闭锁力就是定向钮所受接触力在X 轴的分量FX。摩擦力在X 轴的分量为f,通过查看摩擦力在闭锁力中所占比例,得到摩擦条件对闭锁力的影响。当闭锁机构螺栓的拧紧力矩为6 N·m 时,根据式(1)施加2 400 N 预紧力,得到的定向钮沿射向(即X 轴方向)的受力曲线如图4 所示。
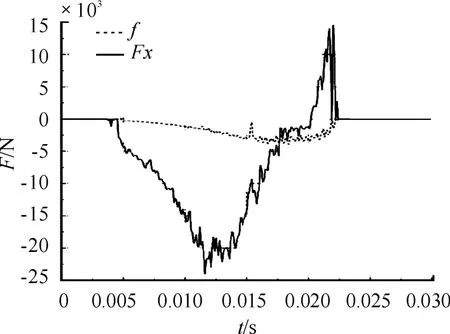
图4 拧紧力矩为6 N·m 时定向钮受力曲线
提取几个时刻的定向钮和闭锁机构作用位置,如图5 所示,以及闭锁机构右端开口Y 轴方向位移曲线,如图6 所示,定向钮沿射向的速度与加速度曲线,如图7 所示。

图5 定向钮与闭锁机构相对位置变化

图6 闭锁机构右端开口Y 轴方向位移

图7 定向钮速度与加速度曲线
从图4 可以看出,定向钮在0 到3.7 ms 不受约束力,这段时间是定向钮在推力作用下开始运动,与闭锁机构消除初始间隙;从3.7 ms 到22.5 ms 为定向钮与闭锁机构相互作用时间;其中,从3.7 ms 到11.6 ms 约束力一直在增加,图5 表明,这段时间内,定向钮沿卡簧右端AB 段滑动,由于AB 段为平面,所以定向钮所受接触压力垂直于AB 面指向定向钮轴心。随着卡簧被推开,其弹性势能越来越大,回弹力也在增大,故定向钮所受约束力沿X 轴分量也就越来越大,并且11.6 ms 时约束力达到最大值24 030 N,此时摩擦力贡献的闭锁力为1 803.52 N,所占比例为7.5%。从11.6 ms 到17.7 ms,约束力逐渐下降,这是因为定向钮上的受力点由C点慢慢滑动至D 点,接触压力与X 轴负向的夹角越来越大,使得接触压力在X 轴分量越来越小,因此定向钮X 轴向所受约束力也越来越小。从17.7 ms 到20.1 ms 定向钮正好在上下卡簧之间,图4 中可以看出这段时间摩擦力的绝对值比闭锁力的绝对值大,可以断定这段时间内卡簧对定向钮的接触压力起到往外推挤的力,这段时间定向钮所受约束力比较稳定。从20.1 ms 之后,定向钮挣脱出闭锁体,但是继续与卡簧右端外壁发生接触,所以此时定向钮所受接触力变为X 轴正向。从图6 可以看出,11.6 ms 之前卡簧右端张口速度越来越快,而从11.6 ms 到17.7 ms 之间张口的速度变慢,就是因为从11.6 ms 开始,卡簧E 点与定向钮接触,且沿着圆弧CD 滑行,所以卡簧开口的速度呈现出先大后小的情况。
图7 表明:在定向钮挣脱闭锁器期间加速度一直为正,振荡幅度不大,而图4 中闭锁力振荡比较明显。这是因为闭锁力远远小于火箭弹的推力值,比如10 ms 时,定向钮所受闭锁力为14 768.6 N,而此时的推力值已经达到82 666.67 N,所以即使闭锁力发生振荡,定向钮的加速度几乎不受影响,总体上是均匀增加的。
根据以上定向钮与闭锁机构相互作用历程分析,本文认为,定向钮在射向所受的最大约束力就是闭锁机构在发射时所提供的闭锁力。
4 结论
本文针对某新型火箭炮闭锁机构,首先通过试验测试了其闭锁力,然后运用非线性有限元动力学方法,计算了发射条件下定向钮与闭锁机构之间相互作用历程,得到以下结论:通过试验测试该闭锁机构的闭锁力,测试结果说明该闭锁机构在适当的拧紧力矩下能够达到闭锁力设计值。通过对闭锁机构仿真分析,得到该闭锁机构在发射条件下,当拧紧力矩为6 N·m 时,闭锁力的大小为24 030 N。
[1]贺北斗,林永明,曹听荣.火箭发射装置设计[M].北京:国防工业出版社,1988.
[2]陈四春.火箭炮闭锁机构工作过程瞬态动力学分析[J].南京理工大学学报,2014,38(5):608-614.
[3]姜勇,杨全,乐贵高.某火箭炮闭锁挡弹器结构设计与仿真分析[J].弹箭与制导学报,2011,31(50):119-122.
[4]李军,马大为,曹听荣.火箭发射系统设计[M].北京:国防工业出版社,2008.
[5]杨叔子,李斌,张福润.机械加工工艺师手册(单行本机械装配)[M].北京:机械工业出版社,2012.
[6]吴茂林,梁洪涛. 某弹簧式闭锁机构分析与仿真[J].四川兵工学报,2014(8):5-7.

