关于工程造价指数预测模型的探讨
邱国林 张荣芳
(吉林建筑大学管理学院,长春 130118)
关于工程造价指数预测模型的探讨
邱国林 张荣芳
(吉林建筑大学管理学院,长春 130118)
工程造价指数的预测研究对工程造价的动态管理具有重要作用,本文以灰色预测模型作为工程造价指数的预测模型,运用天津市历史造价指数对模型的预测精度进行检验,通过实例验证该模型的预测精度较好。
工程造价;预测模型;灰色理论
建设工程一般具有建设周期长、造价高的特点,市场价格波动造成工程造价不断变动,编制工程造价指数是对已完建设工程的造价进行分析,若要对工程造价的未来变动趋势有一定的把握,需要对工程造价指数进行预测研究。工程造价指数的预测能实现真正意义上的造价动态管理,为准确确定工程造价、降低经营风险具有重要作用,同时为工程建设的各参与方提供造价控制依据,也为国家制定宏观调控措施提供依据。
1 灰色GM(1,1)预测模型
灰色GM(1,1)模型的构建
第一步:
原始数列的起伏变化通过一次累加弱化了原始数列的起伏,生成的数列呈现递增形式。
第二步:
假设x(1)满足一阶微分方程
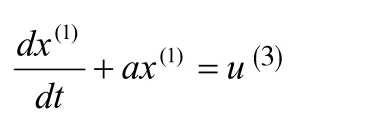
其中a,u为常数,称a为发展灰数,u为内生控制灰数,是对系统的常定输入。
当方程满足初始条件 t=t0时,的解为
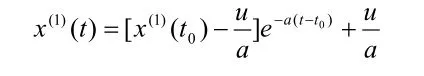
对等间隔取样的离散值(0t=1)则为
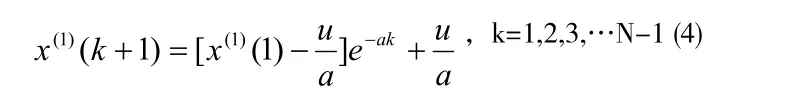
第三步:
最小二乘法估计常数a和u
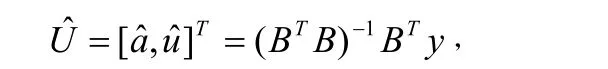
其中
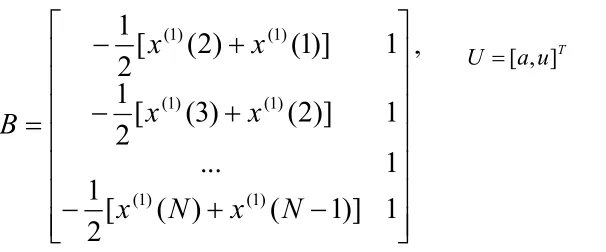
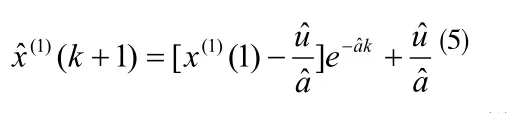
2、模型的检验
(1)残差检验
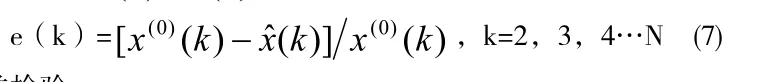
(2)后残差检验
x(0)的均值:
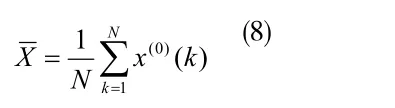
x(0)的方差:
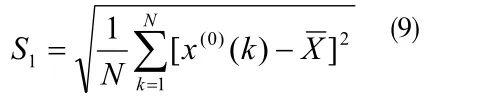
E(k)的均值:
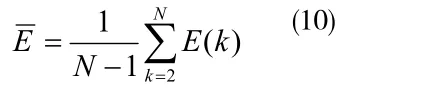
E(k)方差:
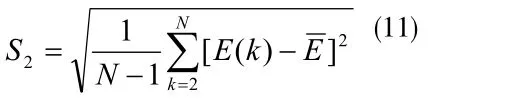

模型预测精度等级评级表
3灰色GM(1,1)预测模型的实例分析
本文以天津市建筑工程造价月指数为例进行GM(1,1)预测模型的实例分析,并预测2015年1月和2月的造价指数。

天津市高层框架结构建筑工程造价月指数
来自天津市工程造价信息网
第一步:收集原始数列
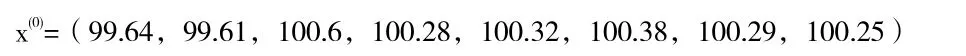
将其累加一次得
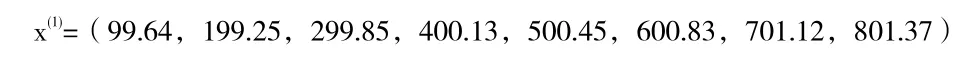
第二步:对x(1)作紧邻均值生成
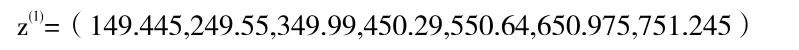
第三步求累加生成矩阵B和向量y

第四步:确定GM(1,1)灰色微分方程由

第五步:解GM(1,1)灰色微分方程
第六步解x(1)的模拟值
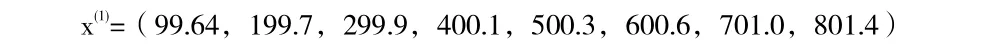
还原x(0)的模拟值
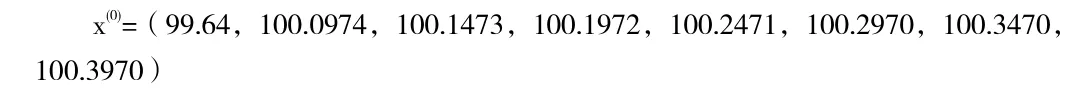
预测模型的模拟数值与实际数值的对比及相对误差率见表1-1。
检验计算标准差 C=0.000859,小误差概率 P=1,对比精度等级评价表,精度等级为好,所以GM(1,1)可用于工程造价指数的预测中。
根据预测方程计算的2015年1月和2月的造价指数分别是100.447、100.497,相对误差率分别为0.35%、0.9%,预测的精度比较好。

天津市高层框架结构建筑工程造价月指数预测分析表 表1-1
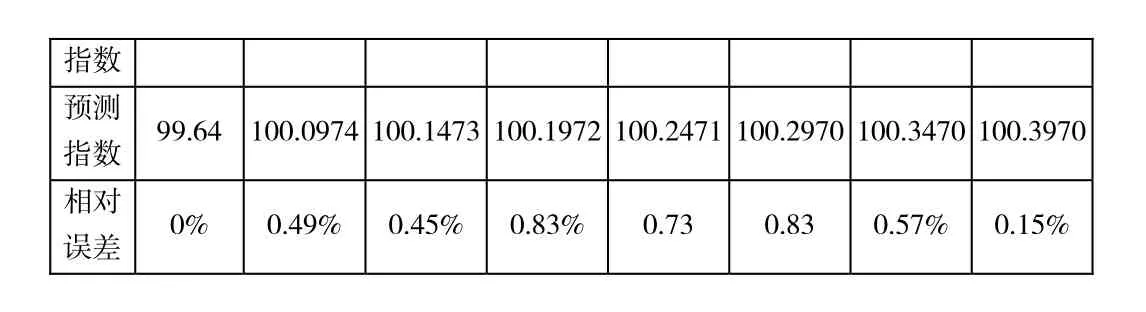
指数预测指数 99.64 100.0974100.1473100.1972 100.2471 100.2970100.3470100.3970相对误差 0% 0.49% 0.45% 0.83% 0.73 0.83 0.57% 0.15%
实际指数与预测指数对比图
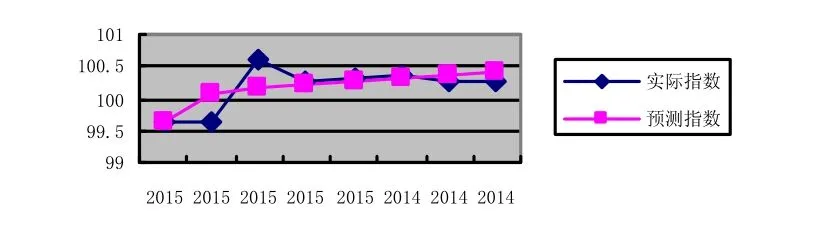
3结语
将预测理论运用到工程造价指数中,通过对工程造价指数的预测对未来工程造价的变动趋势进行分析,对促进我国工程造价控制理论的发展具有重要作用。通过对灰色预测模型在造价指数预测中的实例验证,灰色预测模型以小样本建模,适用于工程造价指数的短期预测,预测精度比较好。
[1]徐国祥主编,统计预测和决策,上海财经大学出版社,1998年06月第1版.
[2] 陈丛发,闫明相,陈涛. 建设工程造价指数预测研究[J]. 建筑经济,2014,09:52-55.
TU43
B
1007-6344(2015)08-0224-02
邱国林1(1964.04.27),男,吉林省长春市人,教授,
张荣芳2(1990.12.09),女,山东省临沂市人,吉林建筑大学管理学院在读硕士研究生

