基于滑模控制算法的船舶动力定位系统控制仿真研究

孙好好，肖健梅，王锡淮

(上海海事大学 物流工程学院，上海 201306)

基于滑模控制算法的船舶动力定位系统控制仿真研究

孙好好，肖健梅，王锡淮

(上海海事大学 物流工程学院，上海 201306)

针对船舶动力定位控制系统非线性的特点及控制过程难以优化，性能易随外界环境及负载变化而改变，本文提出了一种基于滑模控制算法的船舶动力定位系统控制方法。首先，探讨了动力定位系统数学模型的选取；然后介绍了滑模控制方法的原理及具体算法；最后通过Simulink对该算法进行了仿真验证，验证了滑模控制算法对船舶动力定位系统控制的有效性。

滑模控制 非线性 船舶动力定位 数学模型

0 引言

船舶动力定位系统简称DPS(Dynamic Positioning System)，是为了克服传统锚泊的应用局限性所提出的一种能根据船舶自身的动力系统克服风、浪、流等环境外力(矩)的干扰，使船舶保持在一定位置和方向的系统[1]。动力定位技术相比传统的锚泊定位，具有定位精度更高、灵活性更好、适用于多种海况、操作方便、机动性强等优点，对海军现代化建设及海洋开发均具有重要意义[2]。

控制器、测量及推力系统是动力定位系统的三个主要组成部分，而控制器技术促进动力定位不断发展[3]。船舶的运动具有非线性强、大时滞、大惯性、强耦合的特点[4]。本文将滑模控制算法应用于船舶动力定位系统中，将实际输出值与设定的目标输出值作差，并把差值作为滑模控制器的输入进行控制器设计。仿真结果验证了滑模控制器对于动力定位系统具有良好的控制性能。

1 船舶动力定位系统数学模型的建立

1.1 船舶运动学模型的建立

建立水平面三自由度大地坐标系NOE和船舶随体坐标系xoy，xoy相对于NOE的速度为v=[u v r]T，船舶在坐标系中的位置和艏向为η=[x y ψ]T，假设所研究船舶左右对称，xoy坐标系原点选于船体重心处，如图1所示。

图1 大地与船体坐标系

随船坐标系和地球坐标系上的速度之间有以下转换关系：

1.2 船舶动力学模型的建立

2 船舶动力定位系统滑模控制器的设计

2.1 滑模控制算法

滑模控制实际上是一种不连续的非线性控制策略，可以让系统沿规定的状态轨迹作高频率、小幅度的上下运动，即滑动模态或“滑模”运动。这种滑模运动与系统的各种参数以及外界干扰无关，因此滑模运动系统的鲁棒性很好[6]。

滑模控制的基本问题可作如下描述，设存在一控制系统进而求解系统的控制函数

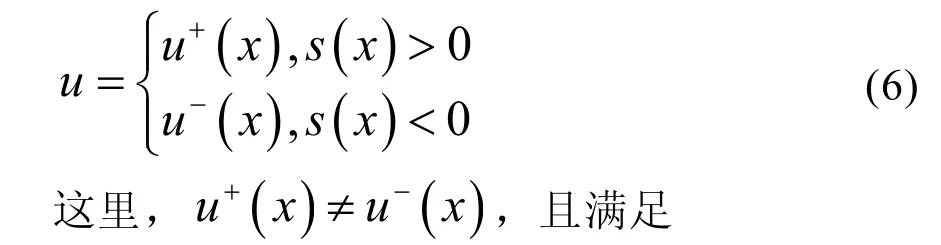
1) 式(6)成立，即滑动模态必须存在；

2) 可达性条件：切换面s（x）=0以外的运动点将于有限的时间内全部到达该切换面；

3) 保证滑模运动稳定；

4) 满足控制系统动态品质的要求。

2.2 滑模控制器设计

船舶动力定位滑模控制器设计如下，由式(3)可得：

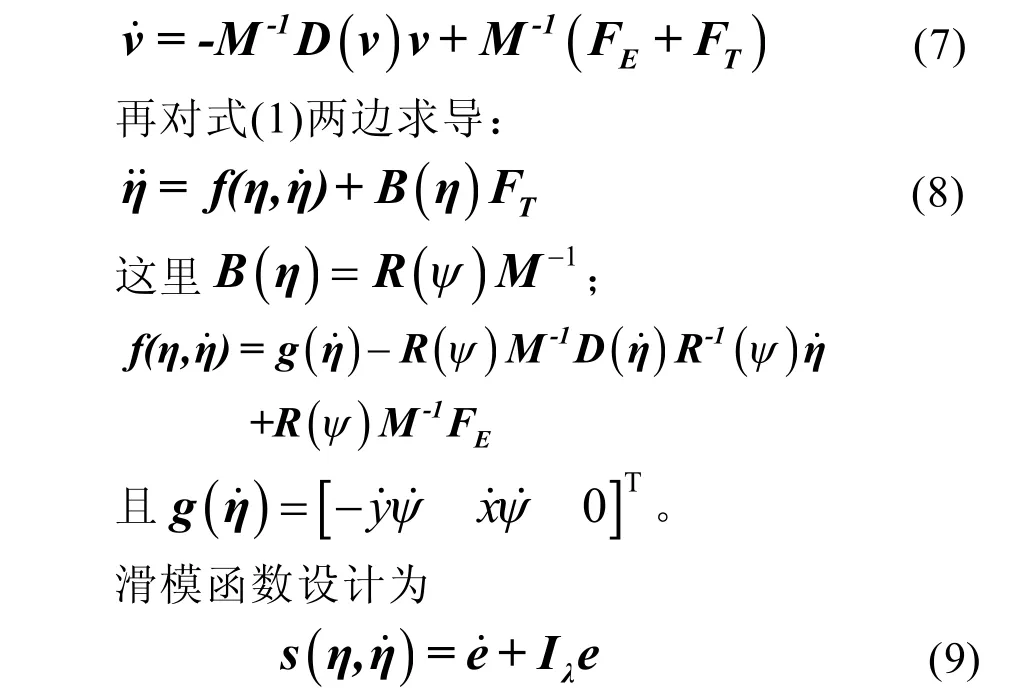
2.3 滑模控制器参数整定

在滑模控制器中，参数λi受到以下三个方面限制：共振频率fR，时间延迟TA及采样率fs，分别为

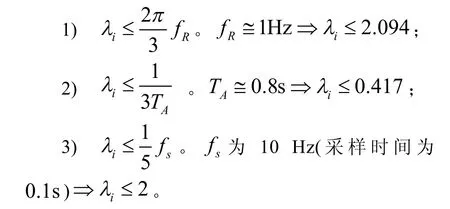
由以上三个限制取λ1= λ2= λ3=0.4。

边界层厚度由式(10)确定，且在纵荡、横荡、艏摇三个方向上跟踪误差分别为0.12 m、0.12 m 和50。因此边界层厚度相应分别为0.05、0.05和0.035。

3 仿真及结果

本文以一艘动力定位船舶为研究对象进行仿真研究。该船长175 m，质量为2.460962×107，船舶可逆惯量矩阵和正定线性阻尼矩阵分别为[8]：

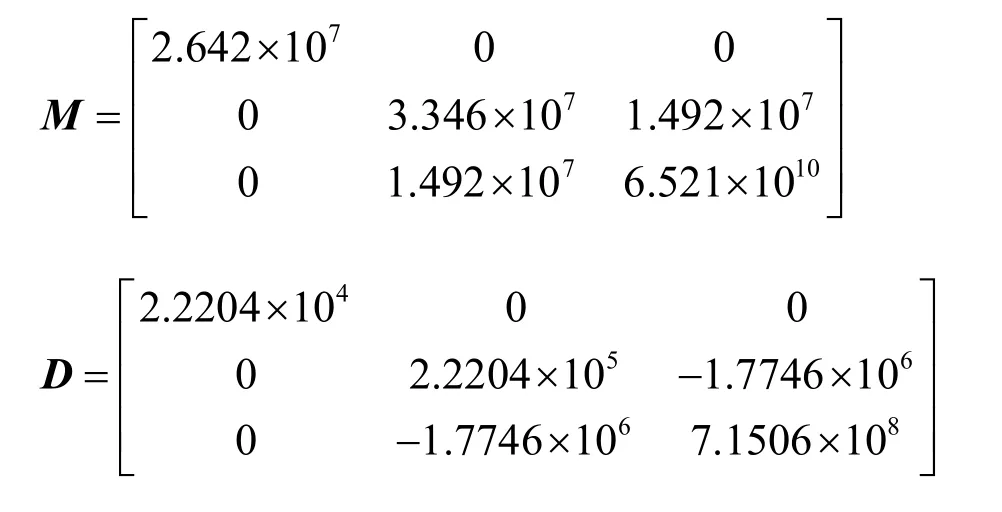
在仿真中，设定船的目标位置为ηd=[15m 10m 80]T，初始位置为η0=[0m 0m 00]T，初始速度为v=[0 0 0]T。外界环境(风浪流)对系统造成的干扰力(矩)可描述如下，即常值干扰信号叠加正余弦时变干扰信号[8]：

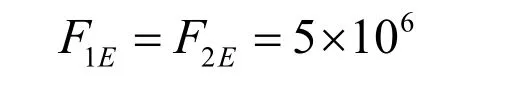
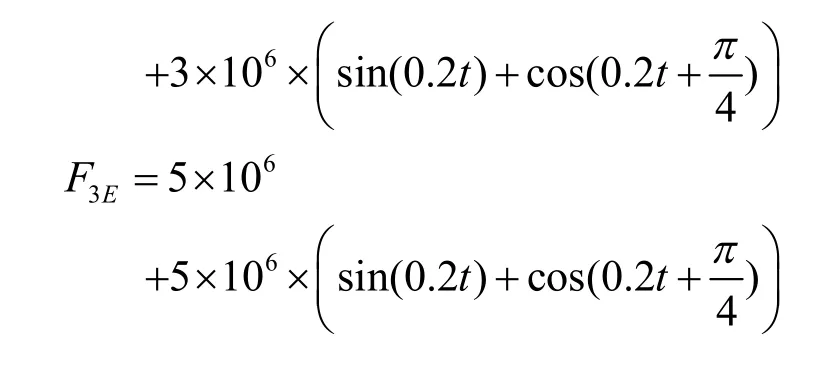
控制系统仿真结果如图2、3和4所示。

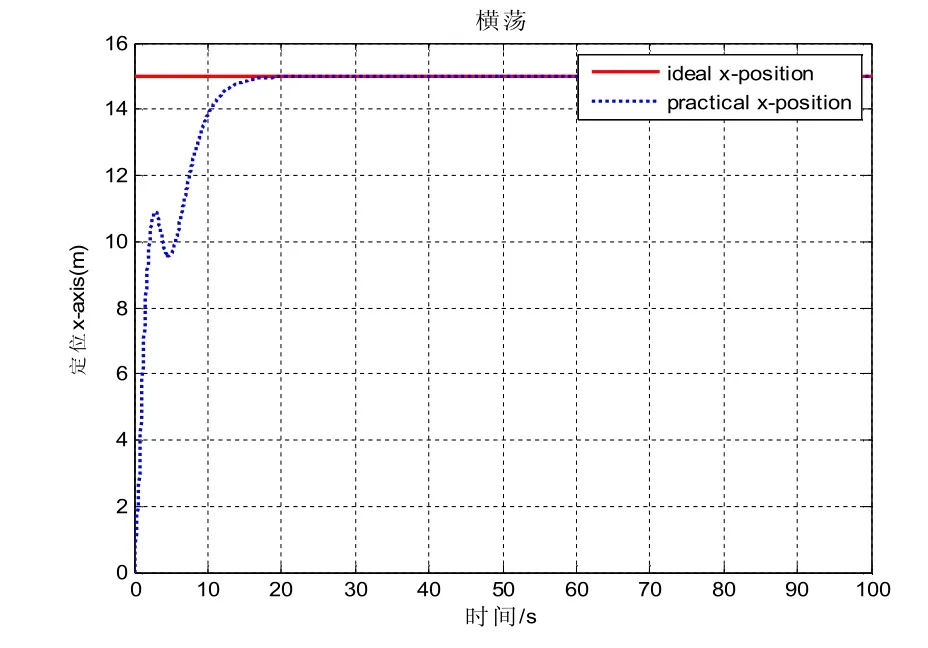
图2 船舶横荡仿真曲线

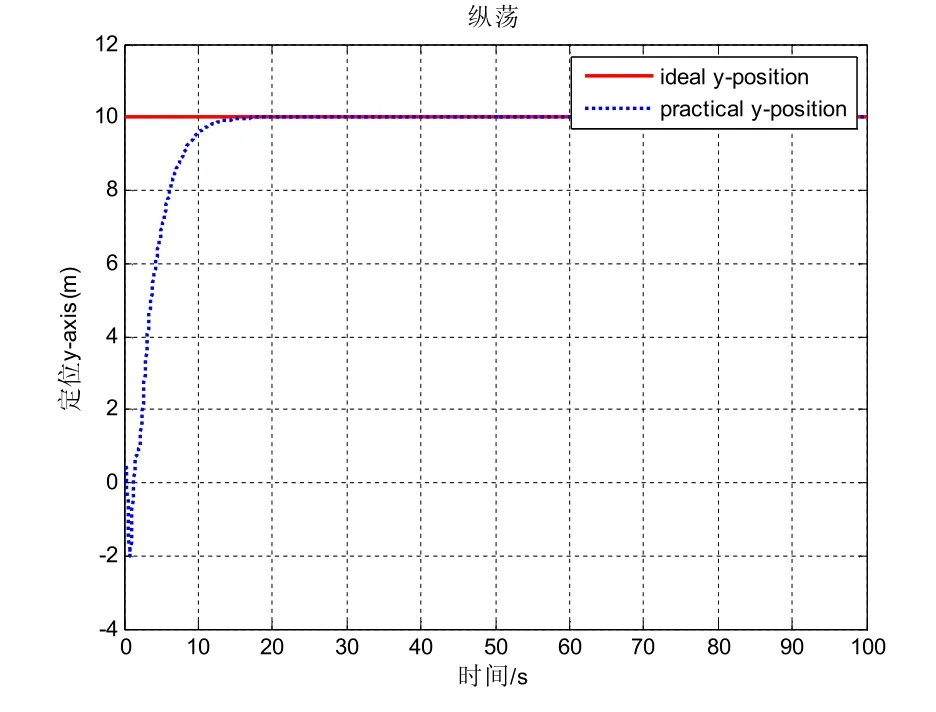
图3 船舶纵荡仿真曲线

图4 船舶艏摇仿真曲线

4 结论

本文将滑模控制算法应用于船舶动力定位系统中，并通过MATLAB对控制器进行了设计仿真。由仿真结果可知，基于滑模控制算法设计的控制器，可使船舶在25 s内准确地从坐标原点到达目标定位点(15m 10m 80)，在纵荡、横荡和艏摇方向上都有很好的控制效果，达到了进行实时控制的目标，控制精度较高，且滑模控制系统具有较好的鲁棒性和稳定性，对于实际工程项目具有很高的应用价值。

[6] 李郡, 肖健梅, 王锡淮. 基于预测函数算法的船舶动力定位系统控制 [J].中国水运(下半月), 2014.5.

[7] 边信黔, 付明玉, 王元慧. 船舶动力定位 [M]. 北京∶科学出版社, 2011.

[1] Fossen T. Guidance and control of ocean vehicles [M].New York∶ Wiley, 1994.

[2] 余培文, 陈辉, 刘芙蓉. 船舶动力定位系统最优控制器的仿真设计[J]. 船海工程, 2009,38(4)∶ 118-120.

[3] E.A. Taannuri. Dynamic positioning systems∶ An experimental analysis of sliding mode control[J]. Control Engineering Practice, 2010.

[4] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京∶清华大学出版社, 2012.10.

[5] Swarup Das. Applicability of sliding mode control in autopilot design for ship motion control [C]. IEEE International Conference on Recent Advances and Innovations in Engineering, 2014.5.

[6] 杜佳璐. 基于动态面控制的船舶动力定位控制律设计[J]. 交通运输工程学报, 2014.10.

[7] 孟浩. 基于终端滑模的欠驱动船舶航迹跟踪鲁棒控制[C]. 第三十二届中国控制会议论文集, 2013.7.

Simulation of Ship's Dynamic Positioning Systems Control Based on Sliding Mode Control

Sun Haohao, Xiao Jianmei, Wang Xihuai

(School of Logistics Engineering College, Shanghai Maritime University, Shanghai 201306, China)

Ship's dynamic positioning system is nonlinear and difficult to be optimized, and its performance varies with environmental or loading conditions. To solve the problem, a sliding mode control is proposed in ship's dynamic positioning system. Firstly, the selection of mathematical model of ship's dynamic positioning system is discussed. Then, the principle of sliding mode control method in detail and concrete algorithm is introduced. Finally, the algorithm is verified through Simulink. Simulation results verified the effectiveness of the control system of dynamic positioning system.

sliding mode control; nonlinearity; dynamic positioning; mathematical model

TP273

A

1003-4862(2015)08-0029-03

2015-04-09

孙好好（1990-），男。研究方向：复杂系统的控制与优化；肖健梅（1962 -），女，教授。研究方向：智能控制、粗糙集理论、物流系统优化、智能交通系统等；王锡淮（1961 -），男，教授。研究方向：复杂系统建模与控制、系统优化、系统仿真、交通控制工程等。