高超声速数值模拟平台转捩模型的标定
张毅锋,雷净,张益荣,毛枚良,陈坚强
高超声速数值模拟平台转捩模型的标定
张毅锋1,雷净2,张益荣1,毛枚良1,陈坚强1
(1.中国空气动力研究与发展中心计算空气动力研究所,四川绵阳621000; 2.北京临近空间飞行器系统工程研究所,北京100076)
基于CARDC的高超声速流动数值模拟软件平台Chant-2.0,以典型低速平板转捩算例为参考,对γ-Reθ转捩模型的经验关系式进行了标定,并且对压力梯度函数进行了高马赫数修正,在高超平板和尖锥的转捩算例中进行了初步检验,计算结果表明:在高超计算平台上标定的转捩模型,较好地模拟了低速平板流动的转捩起始位置和转捩区长度,经过高马赫数修正后在高超流动转捩模拟中表现出较大的潜力。
高超声速流动;数值模拟;转捩模型;标定
0 引言
Menter等根据低速平板转捩风洞试验,在2002年提出了一种可避免非局部信息的γ-Reθ转捩模型[1-4],该模型没有考虑转捩过程的物理机理,而是依据风洞实验数据将局部湍流度和压力梯度等物理量与转捩动量厚度雷诺数相关联,根据局部涡量雷诺数和临界动量厚度雷诺数的比值判断转捩,在流场中任意一个涡量雷诺数超过局部转捩雷诺数的地方,间歇方程源项被激活并产生湍流。该模型优点是:严格意义上基于局部变量的转捩模型,与现代CFD方法兼容,如非结构网格和大规模并行计算,可以方便地融于一般数值模拟软件中。目前,γ-Reθ模型已经被成功地用于低速翼型、航空器和涡轮流动的转捩数值模拟中[1-5]。
γ-Reθ转捩模型包含三个关键的经验关系式:转捩动量厚度雷诺数Reθt、转捩区长度Flength、临界动量厚度雷诺数Reθc。Reθt关系式是通过低速平板试验得到的Reθt和局部湍流度、压力梯度参数的关系建立的。Menter和Langtry等最初仅给出了Reθt经验关系式,而Flength和Reθc的具体形式则被作为商业秘密直到2009年才在文献[2]中公开。实际上,由于各种CFD计算平台的数值特性不同,Flength和Reθc的具体形式和参数会有所不同,例如Srensen[6]、Suluksna[7]、Martin[8]、张玉伦[9]、牟斌[10]等分别采用不同的经验关系式也都较好地模拟了T3系列低速平板转捩,而为了得到理想的计算结果通常需要在所用计算平台上进行细致的数值标定。
鉴于γ-Reθ模型在低速流动转捩模拟中的成功,如何将该模型用于高超声速流动的转捩模拟正在吸引众多学者研究,例如,Martin等(2008)[8]考虑来流湍流度构造了Flength和Reθc关系式,较好地模拟了M∞=8.3的双楔壁面压力分布。Gray等(2009)[11]对压力梯度和转捩长度关系式进行修正,对M∞=8的尖锥进行了轴对称计算,研究了来流湍流度和网格间距对转捩模拟结果的影响。Khalil等(2012)[12]模拟了轴对称高超圆锥转捩流动,转捩区热流和实验值符合较好。国内,张晓东(2010)[13]、颜培刚(2011)[14]等也进行了类似的数值模拟。
本文以CARDC自主研发的高超声速数值模拟软件平台Chant-2.0为基础,采用γ-Reθ转捩模型和kω SST湍流模型,通过T3系列低速平板数值试验标定了γ-Reθ模型的Reθc和Flength经验关系式,并对转捩模型了进行压力梯度函数的高马赫数修正,在M∞= 4.5平板和M∞=7.93的尖锥转捩流动模拟中进行了初步验证,计算结果表明,高马赫数修正后的转捩模型较好地预测了高速边界层转捩位置,适合高超声速边界层流动转捩的模拟,值得进一步探讨γ-Reθ模型在工程实际中的应用。
1 模型简介
γ-Reθ转捩模型由两个变量输运方程构成:间歇因子γ方程和当地转捩起点动量厚度雷诺数珘Reθt方程。γ表示流动处于湍流和层流的时间比例,γ方程用来触发当地转捩,珘Reθt方程用来捕捉湍流强度的非局部影响和避免经验关系式中所用物理量带来的非局部计算。珘Reθt方程是γ-Reθ模型的核心,它起到将经验公式和间歇方程中转捩起点标准相联接的作用。输运方程的无量纲形式如下:
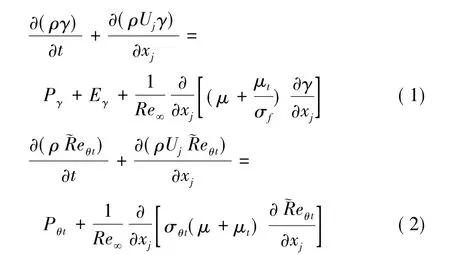
其源项及系数具体见文献[2]。
γ-Reθ模型包含三个关键的经验关系式:转捩动量厚度雷诺数Reθt、转捩区长度Flength、临界动量厚度雷诺数Reθc。Reθt是湍流度Tu和压力梯度参数λθ的函数,本文采用Menter等[2]给出的Reθt经验关系式。Flength和Reθc对数值计算平台的依赖性很强,特别是计算格式,它们通过数值试验标定获得,下一节详细介绍标定过程。
γ-Reθ模型和k-ω SST湍流模型的结合,是通过有效间隙因子对湍动能k方程生成项和耗散项的作用来实现,转捩模型效果最终由涡粘系数来实现。
计算边界条件为,物面:γ和珘Reθt的法向通量为零;自由流入口:γ=1,珘Reθt通过Reθt经验公式计算,取λθ=0;出口外插。
2 经验关系式的标定
γ-Reθ模型经验关系式标定是依靠数值计算和风洞试验结果的比对来进行的。Menter等建立γ-Reθ模型时的应用对象主要是低速流动,例如涡轮叶片、机翼等,模型经验关系式标定算例是T3系列不可压低速平板试验,来流湍流度涵盖了自然转捩和Bypass转捩。本文将γ-Reθ转捩模型应用到Chant-2.0软件中的目的是实现高超声速边界层转捩的数值模拟,模型标定理应选用高超风洞试验结果,但由于高超声速静音风洞的试验数据比较少,尤其缺乏包含马赫数、湍流度等系列变化的试验结果,所以直接通过高超风洞试验数据进行模型标定是不现实的。因此,本文首先以低速平板试验为参考标定出Reθc和Flength关系式,然后对转捩模型进行高马赫数修正,最终建立高超声速边界层转捩模型。本节首先介绍低速试验的标定过程,参考Menter等提供的平板试验数据,试验条件见表1,S-K和T3A-试验为低湍流度自然转捩,T3A和T3B为高湍流度Bypass转捩。

表1 平板转捩试验的入口条件Table 1Inlet condition for flat plate test case
计算网格见图1,来流入口边界距离平板前缘0.3m,法向远场边界距离平板0.3m,网格规模为291× 121(流向×法向),平板上分布251个点,流向最小间距Δxmin=1.0×10-3m,法向最小间距Δymin=1.0×10-5m,网格y+min<0.1。
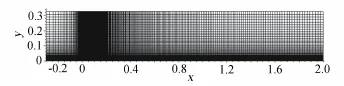
图1 平板计算网格Fig.1Computational grid for flat plate
来流湍流度会随流动而衰减,涡粘性比(μt/μ)∞越小湍流度衰减越快,为保证平板前缘处的湍流度(表1),按照Langtry给出的自由流湍流衰减率计算入口处的湍流度,见下式:

Reθc和Flength是通过数值试验得到的,其形式并不唯一,不同学者出发点不同所采用的函数变量和系数也不相同,比如,Langtry等[2]采用的Reθc为:

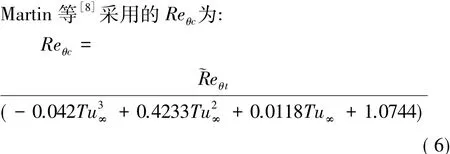
本文采用Langtry等的多项式函数形式,认为Reθc和Flength仅是珘Reθt的函数,标定过程如下:1)将Reθc和Flength作为常数,指定一系列的数值对4个平板算例进行初步试算,观察计算结果的变化规律,当计算摩阻和试验值匹配较好时确定转捩位置处珘Reθt的值,对应的Reθc和Flength就作为这个珘Reθt的函数值,见表2; 2)以珘Reθt为自变量,将4个平板算例最优的Reθc和Flength值拟合成多项式,建立Reθc(珘Reθt)和Flength(珘Reθt)的函数关系式;3)将函数关系式代入模型中进行测试,适当调整系数使得4个平板算例都能给出较好的计算结果。最后标定出的关系式见曲线图2。
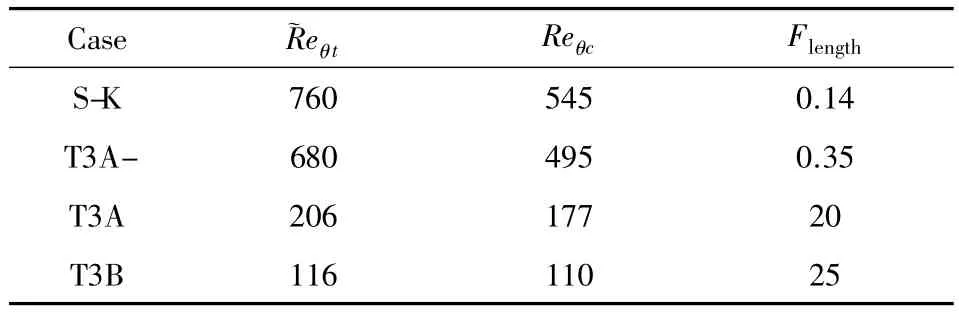
表2Reθc和Flength的数值试验优化参数Table 2Numerical test results for Reθcand Flength

图2拟合后的Reθc~珟Reθt、Flength~珟Reθt函数曲线图Fig.2Reθc~珟Reθt,Flength~珟Reθtfunction curve
图3 为S-K算例边界层中转捩起点动量厚度雷诺数珘Reθt和间歇因子γ的分布图。可以看到,珘Reθt从自由流中逐渐扩散到边界层中,并且沿流向逐渐减小,间歇因子γ在边界层中逐渐增长直到转捩,γ值的分布图与张玉伦等[9]低速软件平台Trip的计算结果相类似。
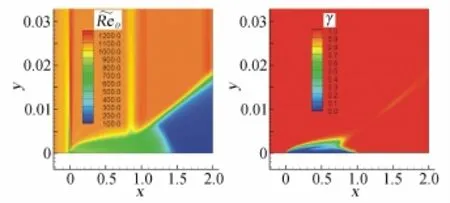
图3S-K算例的珟Reθt和γ的分布图Fig.3珟Reθtand γ distribution for S-K case
经验关系式标定后的平板计算结果见图4,摩阻与风洞试验值和Menter的计算结果进行了比较,同时给出了全层流和全湍流的计算值。本文计算的转捩起点位置和转捩区长度都与试验结果吻合得很好,说明经验关系式的标定很成功。T3B算例转捩前摩阻比试验值高,这可能和来流涡粘性较高有关。
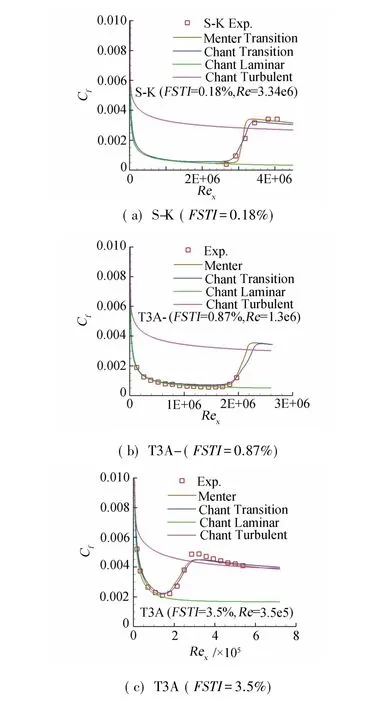
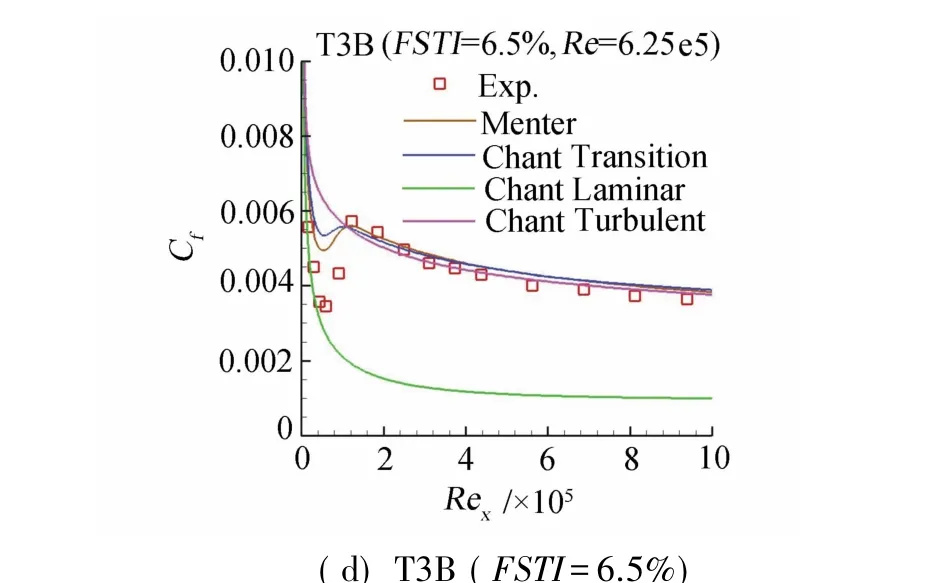
图4 平板摩阻分布的比较Fig.4Distribution of skin friction coefficient
3 高马赫数修正
高超声速流动和低速流动相比,一个显著特征是流动马赫数很高,由此带来高超声速流动所特有的激波、熵层、边界层增厚等一系列物理问题,其中由于边界层变化带来的粘性干扰对压力梯度的影响较大,而边界层转捩对压梯度十分敏感,逆压梯度促发转捩,顺压梯度延缓转捩。
前面进行的经验关系式标定是基于低速风洞试验数据,如果直接用于高超流动转捩模拟是不合适的,比如,转捩模型中的Reθt经验关系式包含了压力梯度的信息,在高马赫数条件下压力梯度参数λθ会受到马赫数的影响,因此γ-Reθ模型在用于高超转捩模拟中应该适当考虑高马赫数效应。Gray等[11]在高超转捩计算中对压力梯度函数F(λθ)进行了马赫数修正,计算表明马赫数修正对高超尖锥转捩位置的正确预测很关键。我们根据可压缩流动边界层理论,分析了压力梯度参数λθ与速度梯度、动量厚度以及马赫数的关系,近似得到了与Gray类似的压力梯度参数的马赫数修正:
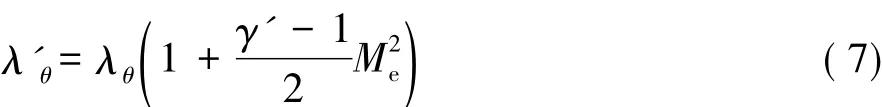
其中:γ'为比热比,Me为边界层外缘马赫数,实际使用中Me取M∞,该方法在下面计算中进行了初步检验。
4 算例验证
算例一为文献[15]中的高超平板流动,来流马赫数M∞=4.5,来流雷诺数Re∞=6.433×106/m,来流温度T∞=61.1K,来流湍流度0.1%。计算网格221× 201,壁面上分布200个点,绝热壁条件。图5为压力梯度参数马赫数修正后的γ和μt分布,与低速平板的分布相似。图6给出了马赫数修正前、后的摩阻分布,并与文献中k-ω-γ转捩模型和DNS结果[15]进行了比较。马赫数修正前预测的转捩位置比较靠后,与k-ω-γ和DNS的结果相差很大,修正后转捩位置前移,转捩起始位置接近于DNS的结果,但转捩后的摩阻与参考值相比偏小,转捩区略长。
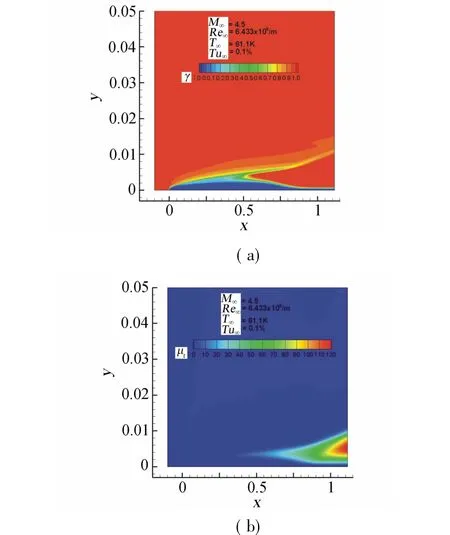
图5 高超声速平板γ和μt的分布Fig.5γ and μtdistribution for hypersonic flate plate
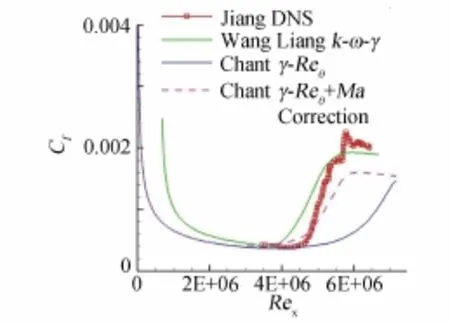
图6 高超声速平板摩阻分布Fig.6Skin friction distribution for hypersonic flate plate
算例二为Kimmel在AEDC B常规风洞中进行的高超尖锥转捩实验[16],模型为半锥角7°的尖头直锥(straight cone,名义压力梯度DPDX=0)和裙锥(flared cone,DPDX=4),来流马赫数M∞=7.93,来流雷诺数Re∞=6.6×106/m,来流温度T∞=53.18K,壁面温度Twall=303.24K,来流湍流度取Tu∞=1%,攻角0°。计算网格:145×201×31。图7和图8分别为直锥和裙锥的壁面压力和热流分布。裙锥在x>0.5以后出现较大逆压梯度。通过与实验[16]、计算[11-12]的St数比较,可以看到,马赫数修正前直锥和裙锥的模拟都没有出现转捩,修正后才能模拟出转捩过程,转捩起始位置和转捩区大小与实验比较接近。

图7 高超声速直锥壁面压力和热流分布Fig.7Pressure and heat transfer distribution for hypersonic straight cone(DPDX=0)
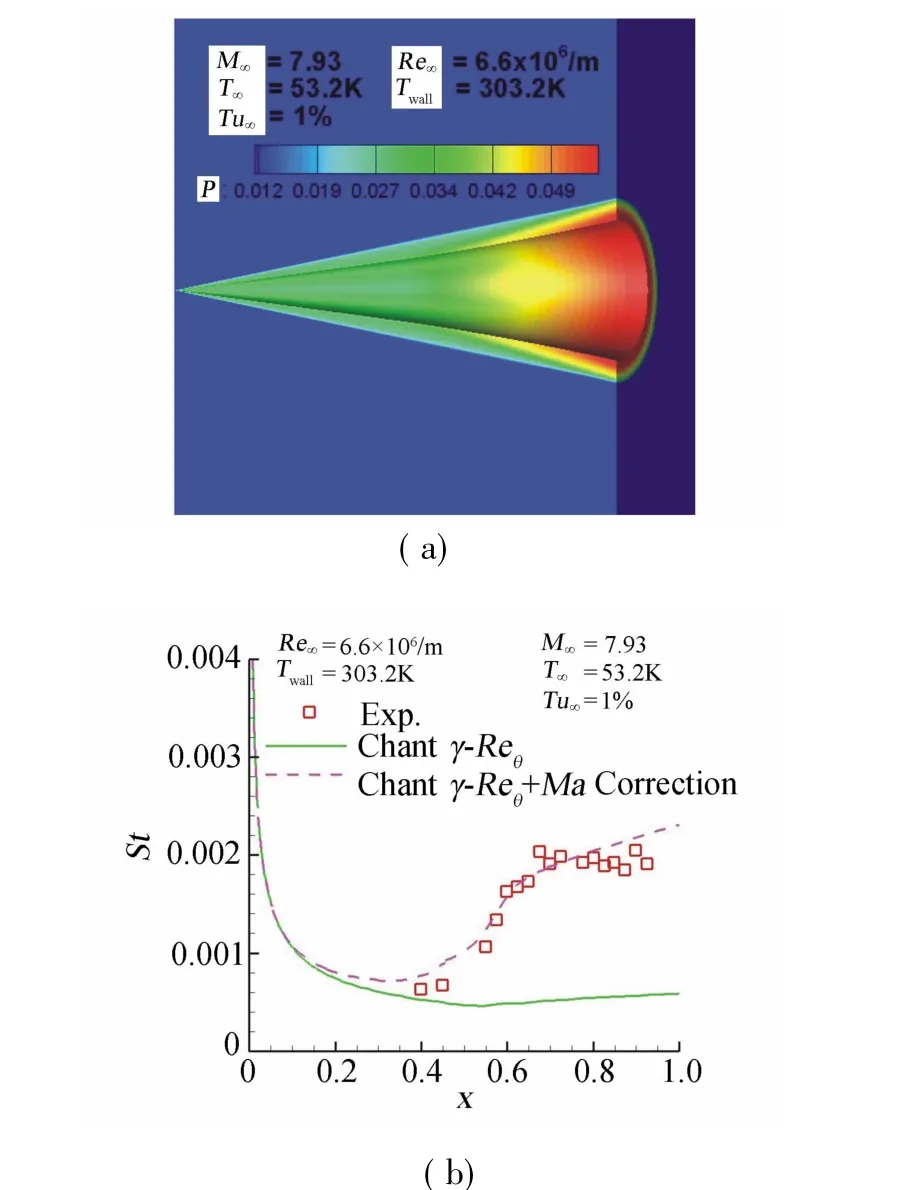
图8 高超声速裙锥壁面压力和热流分布Fig.8Pressure and heat transfer distribution for hypersonic flare cone(DPDX=4)
5 结论
通过不同来流条件下低速平板算例的大量数值试验,我们以高超声速数值模拟软件平台Chant-2.0为基础,对γ-Reθ转捩模型的经验关系式Reθc和Flength进行了成功的标定,取得了与试验数据符合较好的计算结果,并且针对高超声速转捩问题,对原有模型进行了高马赫数修正,在M∞=4.5平板和M∞=7.93的尖锥上进行了初步验证,较好地模拟了转捩位置,说明修正后的γ-Reθ模型具有模拟高超声速转捩的能力,值得进一步深入研究。下一步,我们将在三维高超流动转捩上继续开展转捩模型的修正研究,希望能够使γ-Reθ模型在复杂高超声速转捩模拟中具有工程实用价值。
[1]Menter F R,Langtry R B,Likki S R,et al.A correlation-based transition model using local variables—part I:model formulation[J].Journal of Turbomachinery,2006,128:413-422.
[2]Langtry R B,Menter F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamic codes[J].AIAA Journal,2009,47(12):2894-2906.
[3]Langtry R B,Menter F R.Transition modeling for general CFD application in aeronautics[R].AIAA 2005-522.
[4]Langtry R B,Menter F R,Volker S.Transition modeling for general purpose CFD codes[J].Flow Turbulence Combust,2006,77:277-303.
[5]Atsushi Toyoda,Takashi Misaka,Shigeru Obayashi.An application of local correlation-based transition model to JAXA high-lift configuration model[R].AIAA 2007-4286.
[6]Niels N Srensen.CFD modeling of laminar-turbulent transition for airfoils and rotors using the γ-Reθmodel[R].AIAA 2008-7323.
[7]Keerati Suluksna,Pramote Dechaumphai,Ekachai Juntasaro.Correlations for modeling transitional boundary layers under influences of freestream turbulence and pressure gradient[J].International Journal of Heat and Fluid Flow,2009,30:66-75.
[8]Martin Krause,Marek Behr,Josef Ballmann.Modeling of transition effects in hypersonic intake flows using a correlation-based intermittency model[R].AIAA 2008-2598.
[9]张玉伦,王光学,孟德虹,等.γ-Reθ转捩模型的标定研究[J],空气动力学学报,2011,29(3):295-301.
[10]牟斌,江雄,肖中云,等.γ-Reθ转捩模型的标定与应用[J].空气动力学学报,2012,31(1):103-109.
[11]Gary Cheng,Robert Nichols,Kshitij D Neroorkar,et al.Validation and assessment of turbulence transition models[R].AIAA 2009-1141.
[12]Khalil Bensassi,Andrea Lani,Patrick Rambaud.Numerical investigations of local correlation-based transition model in hypersonic flows[R].AIAA 2012-3151.
[13]张晓东,高正红.关于补充Langtry的转捩模型经验修正式的数值探讨[J].应用数学和力学,2010,31(5):544-552.
[14]颜培刚,韩万金,严红明.应用γ-Reθ湍流模型模拟超声速进气道流动[J].哈尔滨工业大学学报,2011,43(1):95-98.
[15]Wang L,Song Fu.Development of an intermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition[J].Flow Turbulence Combust,2011,87:165-187.
Calibration of transition model for hypersonic numerical simulation platform
Zhang Yifeng1,Lei Jing2,Zhang Yirong1,Mao Meiliang1,Chen Jianqiang1
(1.Computational Aerodynamics Institute of China Aerodynamics Research and Development Center,Mianyang621000,China; 2.Beijing Institute of Nearspace Vehicle’s Systems Engineering,Beijing100076,China)
Based on CARDC hypersonic numerical simulation platform Chant-2.0,applications of γ-Reθmodel to hypersonic boundary layer transition are investigated preliminarily.The transition onset and length are predicted by solving two transport equations for turbulence intermittency factor and momentum thickness Reynolds number.Firstly,γ-Reθtransition model using local correlation functions is calibrated through four cases of low speed flat flows,and in the process freestream turbulence intensities have a wide range from low level natural transition to high level bypass transition.Then,taking account of flow properties of hypersonic boundary layer,the pressure gradient function used in the transition model's Reθtcorrelation is properly modified for high Mach number flows.Finally,by adopting the new model functions,hypersonic boundary layer transitions of flat and sharp cone are calculated and compared with referrence data.The simulation results indicate that the specially calibrated correlations for hypersonic platform software can accurately predict the onset and length of transition region in low speed cases,and high Mach number correction shows good performance in hypersonic simulations.
hypersonic flow;numerical simulation;transition model;calibration
V211.3
Adoi:10.7638/kqdlxxb-2014.0110
0258-1825(2015)01-0042-06
2014-09-18;
2014-09-30
张毅锋(1975-),男,副研究员,研究方向:高超声速流动数值模拟、高精度数值方法.E-mail:zyf63867@163.com
张毅锋,雷净,张益荣,等.高超声速数值模拟平台转捩模型的标定[J].空气动力学学报,2015,33(1):42-47.
10.7638/kqdlxxb-2014.0110.Zhang Y F,Lei J,Zhang Y R,et al.Calibration of transition model for hypersonic numerical simulation platform[J].Acta Aerodynamica Sinica,2015,33(1):42-47.

