变质量振动系统的求解与分析
杜妍辰, 高 雷, 周燕瑜, 秦 婧
(上海理工大学医疗器械与食品学院,上海 200093)
变质量振动系统的求解与分析
杜妍辰, 高 雷, 周燕瑜, 秦 婧
(上海理工大学医疗器械与食品学院,上海 200093)
对变质量碰撞振动系统进行求解分析,研究系统参振质量变化时对系统动力学的影响.采用渐近法对变质量振动方程进行近似解析求解,并运用龙哥库塔法进行数值计算.结果表明,渐近解析法与数值法响应一致,渐近法对于解非线性系统动力行为是有效的;且由计算结果可知,变质量会使系统响应产生一定的突变.振动方程中的参振质量变化系数和质量变化频率分别影响系统突变的振幅和周期.当参振质量变化系数为零时,系统响应平稳;该系数越大,系统响应的突变振幅也越大.激振频率与质量变化频率比值越大,响应突变的周期越大.
振动;变质量;渐近法;响应突变
日常生活中,大多数系统为多参数非线性系统.若在系统运动过程中,某些参数会随时间变化而变化,该系统则被称为时变系统[1].例如,飞机的整机质量会随燃油的消耗而减小,起重机的吊绳会随其升高而缩短,这些便是参数时变系统.碰撞振动是日常生活中常见的一种现象,其涉及的科学领域非常广泛,如数学、物理、化学、机械工程,甚至生理学和医学.通常,由于参振质量为多体组成,则碰撞振动过程中的参振质量会随时间变化而变化.时变系统的振动问题在理论上和工程应用中都具有重要的研究价值,但国内对于变质量振动系统的研究甚少.
变质量碰撞振动系统多为强非线性动力系统,对于非线性系统周期解的传统解析方法有:传统小参数法、平均法、渐近法、多尺度法等.近似解析法虽然便于分析系统参数对振动系统的影响,但如果要获得高精度解,一般结合解析法和数值法进行计算.常用的数值计算方法是基于Matlab的龙哥库塔法.
对于变参数系统所能采用的近似解析方法有渐近法和平均法[2].平均法是将系统中的解的振幅和相位角看作随时间缓慢变化,将振幅和相位展开成富氏级数,并在一个周期内取平均值进行求解.该方法简单,但精确度不高.本文采用渐近法对方程进行近似求解.渐近法也称三级数法或KBM法,是由前苏联学者包戈留包夫和米特罗波尔斯基提出的[3-4].该方法将方程的解、振幅和相位表示为参振质量变化系数ε的幂级数函数,然后用分离变量法求出这些幂级数函数的未知系数[5].
1 动力学方程及求解
1.1 动力学方程
描述变质量振动系统的动力学方程为
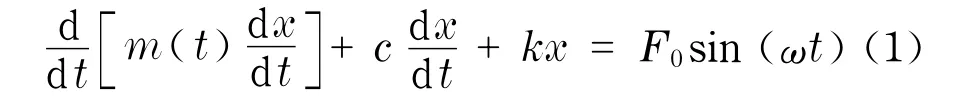
式中,m(t)为系统参振质量;c为阻尼系统;k为刚度系数;ω为激振频率;F0为激振力幅值.
m(t)是一个时变函数,随时间发生变化.对碰撞系统来说,碰撞质量引起的非线性力的变化是缓慢的,因此为了简便计算,m(t)可以用其在一个振动周期中的平均值来代替[6],这里只计入常数项和亚谐波项,省略谐波项部分.可以认为质量围绕某一数值上下波动,其频率常常是系统激振频率的整约数[7-8],并简化得

式中,ε为参振质量变化系数,也称之为小参数;ωa为质量变化频率,ωa=ω/n,n为整数.
对式(2)求导得

1.2 方程的近似求解
对动力学方程采用渐近法求解,式(4)可简化为以下形式


a.振幅A将随着时间t变化;
b.相位角ψ是时间t的非线性函数;
c.方程的解中含有高次谐波成分,有时还含有次谐波.
考虑到非线性作用力的影响,假设式(5)的解为以下形式
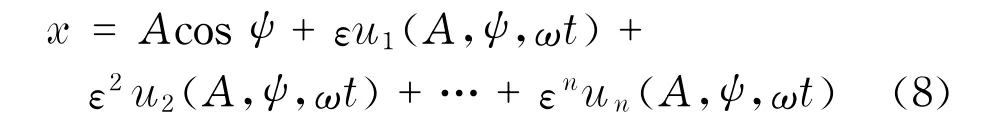
其中,A和ψ是时间t的周期函数,u1(A,ψ,ωt), u2(A,ψ,ωt),…,un(A,ψ,ωt)是以振幅A、相位角ψ及激振频率ω为参数的函数.
假设对非线性系统中的阻尼比δε和固有频率ωε表示为小参数ε的幂级数的形式

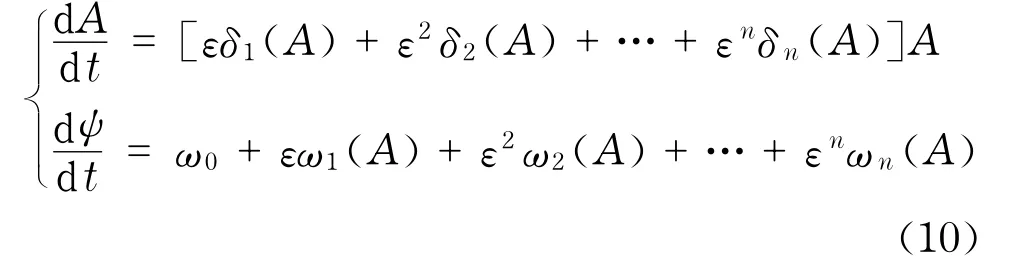
此时,A和ψ对时间的导数不是常数,A和ψ满足
可见,当δ1,δ2…,ω1,ω2…求得后,便可求出A和ψ.
方程的精确度是由求解过程的阶次来决定的,一次近似解有如下形式,只须计算出δ1和ω1即可.

其中,fx′和fx′′是函数f关于位移x和速度x′的一阶导数.令方程两边ε的同一阶的系数相等,可得以下方程
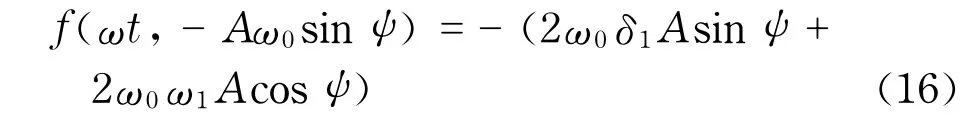
非线性函数f(ωt,-Aω0sinψ)是关于两个变量ψ和ωt且周期为2π的周期函数,将其展开为富氏级数的形式
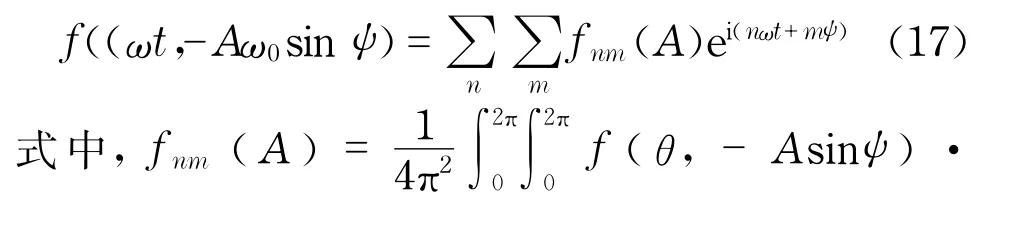

按照三角函数形式展开的傅里叶级数为

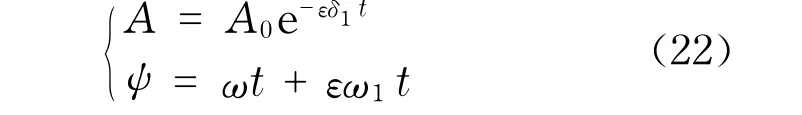
δ1和ω1可由式(20)求出,然后代入式(22)求出A和ψ,把A和ψ的值代入式(11)的第一式,求出响应方程.
1.3 数值求解
采用龙哥库塔法对系统进行数值求解.龙哥库塔法是间接使用泰勒级数展开时的方法,在积分区间内多预设几个点的斜率,然后进行加权平均,作为计算下一点的依据,从而构造了高精度数值计算方法.
记步长H=xk+1-xk,根据微分中值定理有
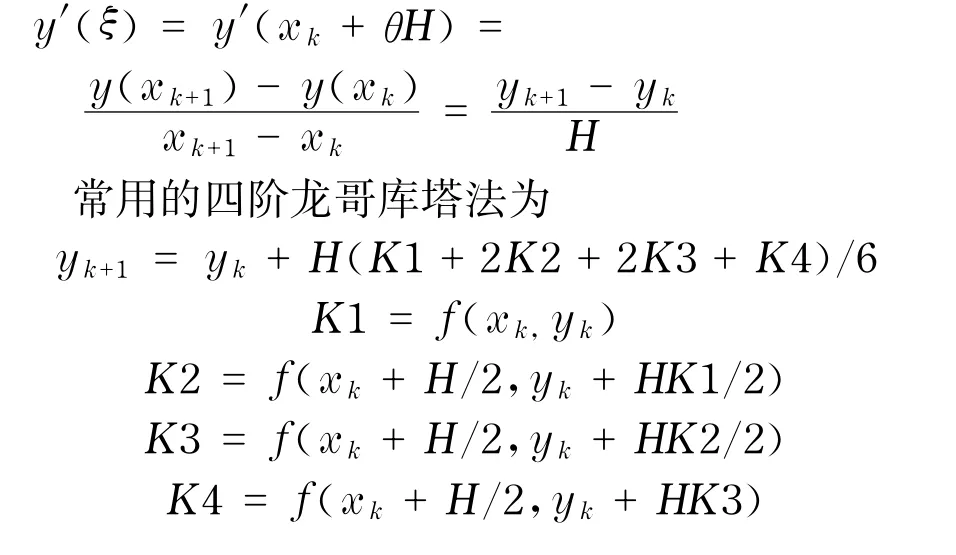
把式(6)带入式(20),并取A的初始值为A0,则由式(21)可求出
按照以上各式,可以从初值(x0,y0)出发计算出y1,y2,…,yk的具体数值.
将变质量振动系统的运动微分方程(5)进行降阶,得到以下等价的二维一阶振动系统

其中,系统的参数值m0=0.1 kg;F0=1.91 N;c= 1.57 N/m;k=37.8 N/m;ω=110.6 rad/s;ωa=ω/ 4;φ=π/4.
2 计算结果
当小参数ε为0.1和0.2时的解析求解和数值求解结果如图1—2所示.
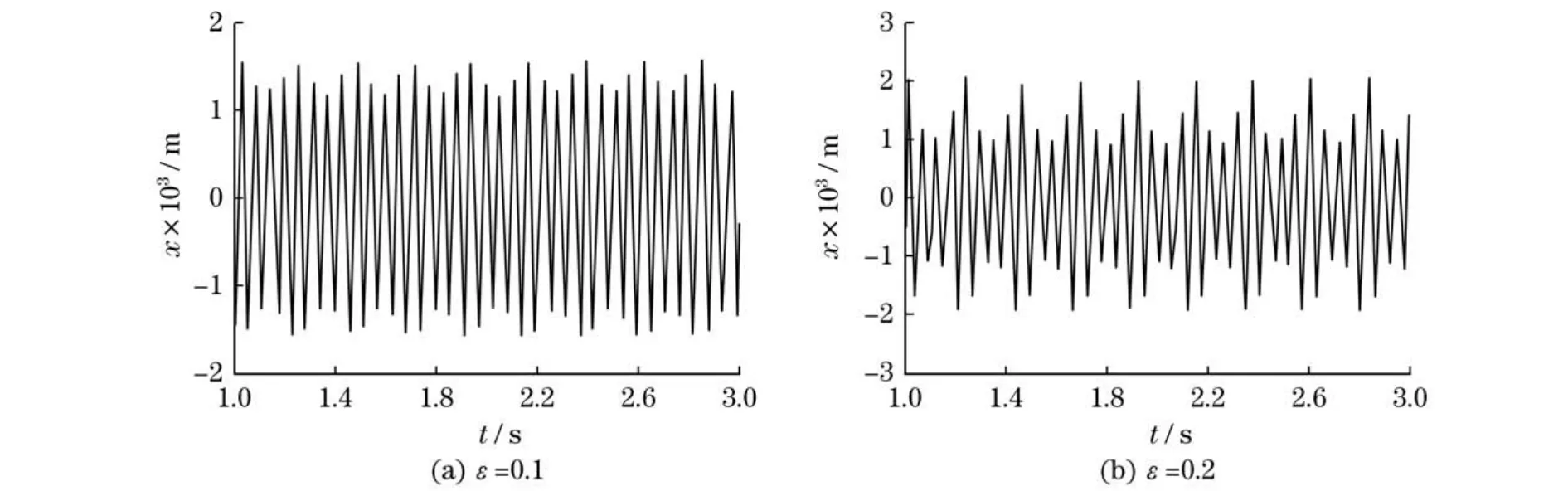
图1 解析计算结果Fig.1 Analytical calculation results
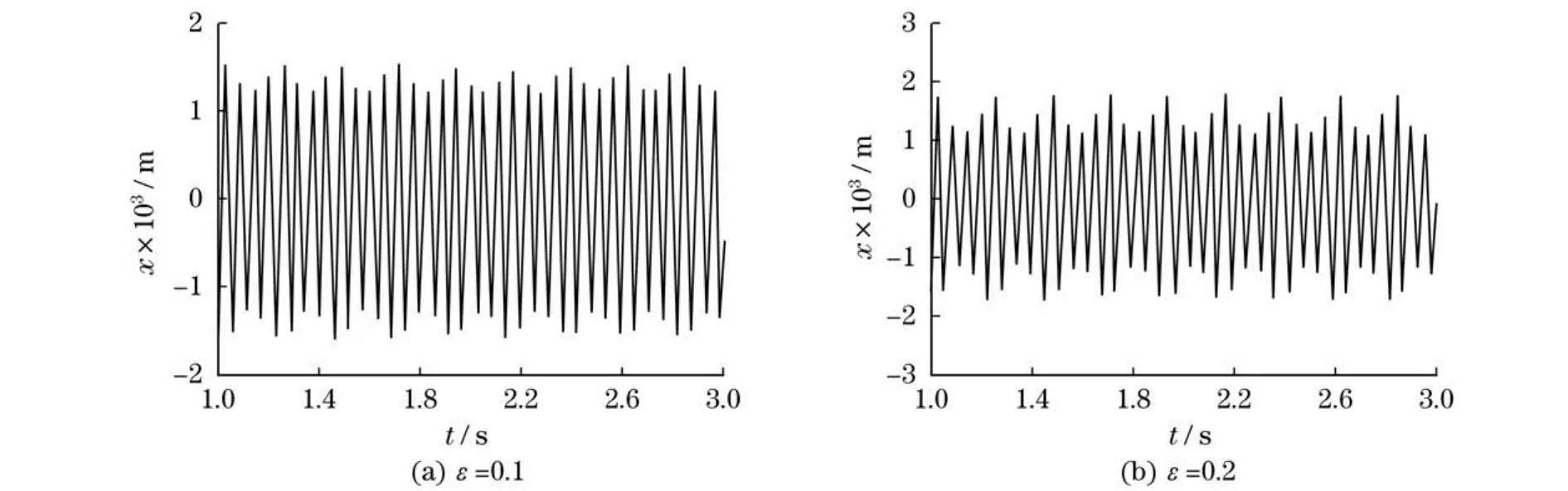
图2 数值计算结果图Fig.2 Numerical calculation results
可以看出,采用渐近法对变质量振动系统进行解析求解所得的振动响应与采用数值法计算的结果是一致的.因此,渐近法用于解决变质量振动问题是有效的.另外,图3给出了ε=0,0.1,0.3时系统中质量变化幅值对系统的影响情况.
以上计算结果表明,变质量振动系统的响应具有一定的周期,参振质量变化系数ε只对系统的突变振幅有影响.ε越大,振动突变幅度越大;ε越小,振动越平稳;当ε为零时,突变振幅为零.所以,为了得到较为平稳的振动响应,应减小式(5)中ε的取值,这和文献[9]得到的结论一致.如果ε过大,在实际运用中将会发生工程事故[10].因此,关于变质量振动的分析对工程实践和理论研究具有重要意义.图4给出了在不同的激振频率与质量变化频率比值下的振动系统响应情况.

图3 振动系统的响应与ε的关系Fig.3 Relation between the system resopne andε
可见,变质量振动系统振动响应的周期随系统激励频率与质量变化频率比值(ω/ωa)的增大而增大,ωa只影响周期,不影响响应振幅的大小.当ωa= ω,周期为零;当质量变化幅值系统一定时,系统振动响应周期与n成正比,即等于参振质量变化的周期.

图4 振动系统响应的时域波形图Fig.4 Diagram of time domain waveform of vibration system response
3 结 论
采用渐近法对变质量振动系统进行解析求解,并与数值计算结果进行比较,所得振动响应一致,说明渐近法用于变质量振动系统是可行的.
变质量振动响应具有周期性,参振质量变化系数ε和质量变化频率ωa分别对系统响应的振幅和周期产生影响.当质量时变方程中的频率一定时,ε取值的不同只影响振动系统响应的幅值,不影响其周期.ε取值越大,振动系统响应的突变性越强;ε越小,系统响应越平稳.当ε一定时,ωa的不同将对振动系统的响应周期有影响.ω/ωa越大,响应周期越大.
[1] 胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000.
[2] Nayfeh A H,Mook D T.Nonlinear oscillations[M]. New York:Wiley,1979.
[3] 包戈留包夫H H,米特罗波尔斯基ЮA.非线性振动理论中的渐近方法[M].金福临,译.上海:上海科学技术出版社,1963.
[4] Minorsky N.Nonlinear oscillations[M].Princeton, New Jersey:Van Nostrand Co.Inc,1962.
[5] 闻邦椿,李以农,韩清凯.非线性振动理论中的解析方法及工程应用[M].沈阳:东北大学,2000.
[6] 王树林,刘美清,胡沂清,等.振动棒磨机非线性振动试验研究[J].机械工程学报,1997,33(4):19-25.
[7] 王树林,李巨光,胡沂清,等.振动棒磨机非线性碰撞振动的建模与分析[J].青岛海洋大学学报,1998,28 (3):157-164.
[8] 卢寿慈.粉体技术手册[M].北京:化学工业出版社, 2004.
[9] Wang S L.Impact chaos control and stress release——a key for development of ultra fine vibration milling[J]. Progress in Natural Science,2002,12(5):336-341.
[10] Huang M H,Thambiratnam D P.Dynamic response of plates on elastic foundation to moving loads[J]. Journal of Engineering Mechanics,2002,128(9): 1016-1022.
(编辑:董 伟)
Solution and Analysis of Vibration System with Variable Mass
DU Yanchen, GAOLei, ZHOUYanyu, QIN Jing
(School of Medical Instrument and Food Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
The solution and analysis of a collision vibration system with variable mass were focused and the influence of vibration mass varying with time on the dynamic behaviors of the collision vibration system was discussed.The asymptotic method was used to solve the vibration equations with variable mass,and the method of Runge Kutta was used for numerical calculation.The results show that the responses calculated by the analytical method and the numerical method are in consistency and the asymptotic method is effective for the solution of the dynamic behaviors of nonlinear systems.The calculation also shows that variable mass will make the system response produce a certain mutation.The variation coefficient and the changing frequency of vibration mass will affect the mutation’s period and the amplitude of system respectively.When the variation coefficient is zero,the system response is stationary.The greater the variation coefficient is,the greater the mutation is.The greater the ratio of vibration frequency to mass varying frequency is, the longer the cycle of response mutation is.
vibration;variable mass;asymptotic method;response mutation
O 328;TB 53
A
1007-6735(2015)05-0462-05
10.13255/j.cnki.jusst.2015.05.009
2014-06-17
国家自然科学基金资助项目(51475308)
杜妍辰(1976-),女,副教授.研究方向:振动控制与应用.E-mail:duyanchen@hotmail.com

