壁面局部振动的二维管内流动分析

许成骅, 王宏光, 朱志文

(上海理工大学上海市动力工程多相流动与传热重点实验室,上海 200093)

壁面局部振动的二维管内流动分析

许成骅, 王宏光, 朱志文

(上海理工大学上海市动力工程多相流动与传热重点实验室,上海 200093)

通过求解二维雷诺时均Navier-Stokes方程,对壁面局部振动的二维管内流场进行数值模拟,分析边界条件在不可压缩计算及可压缩计算情况下对壁面局部振动流动状态的不同影响.研究表明,在不可压缩计算情况下,总压入口条件相对于速度、质量流量入口条件限制少,壁面振动可同时影响振动壁面上、下游的流动参数.在壁面振动管道内,尽管马赫数Ma＜0.3,可压缩流体的流动现象是完全不同于不可压缩流体的.边界条件对于高频振动计算结果的影响比低频振动计算结果的小.因此,在模拟燃气轮机小幅高频振动叶栅的实际工程问题中,必须采用可压缩计算.在相对平缓、充分的入口段条件下,仍然可以采用常规模拟叶片绕流时的速度入口边界条件进行计算.

随着燃气轮机燃气初温的增高,叶片冷却技术研究受到重视.在实际工作中,涡轮动叶片由于高速旋转,并受到静叶尾迹、转子不平衡等因素影响,涡轮动叶片工作在小幅高频的振动状态[1-4],叶片振动会造成流体的扰动,影响流体与振动体表面的传热效果[5-7],因此,认识和掌握振动叶片表面的流动规律,对分析涡轮动叶片的热负荷与可靠性具有重要意义[8].

本文将振动的叶片表面流动问题简化为壁面局部振动的二维管道流动模型,采用Fluent软件进行数值模拟,研究壁面局部振动管道的流动现象,分析计算边界条件在不可压缩及可压缩流动模型情况下对壁面局部振动流动状态的不同影响.

1 壁面局部振动的二维管道计算模型

二维管道流动区域高1 m、长5 m,BF=2 m,振动区域FG=1 m,如图1所示.图2为计算网格,采用全结构化网格,网格总数20万,第一层网格高度0.000 5 m,用标准壁面函数进行近壁处理.

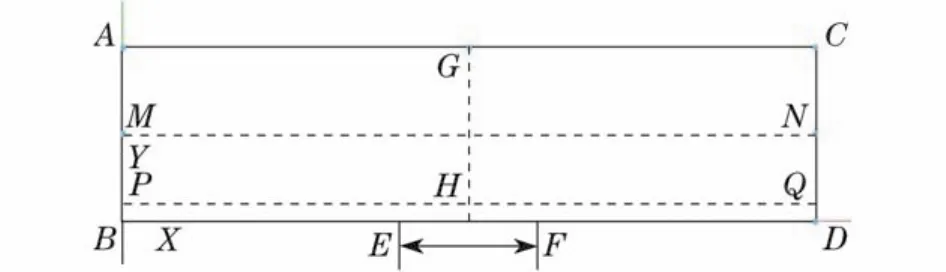
图1 计算区域Fig.1 Calculating area

图2 近壁面计算网格Fig 2 Mesh near the vibrating wall

上下壁面给定无滑移条件.出口边界CD给定静压P1=101 325 Pa.振动区域EF的位移和速度边界条件采用UDF控制[9-11],垂直于主流方向作简谐振动,振型如式(1)所示.

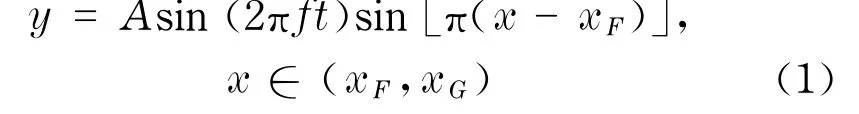
式中,A为壁面振动的振幅;f为振动频率;t为振动时间,x表示以B点为原点的x轴坐标值.

取振动频率f=100 Hz、振幅A=2 mm,选择二阶迎风格式,采用Simple算法.

计算过程中分别对流场中轴线MN以及纵轴线GH进行监控.其中,G,H坐标分别为(2.5,1), (2.5,0).各算例的计算条件如表1所示.

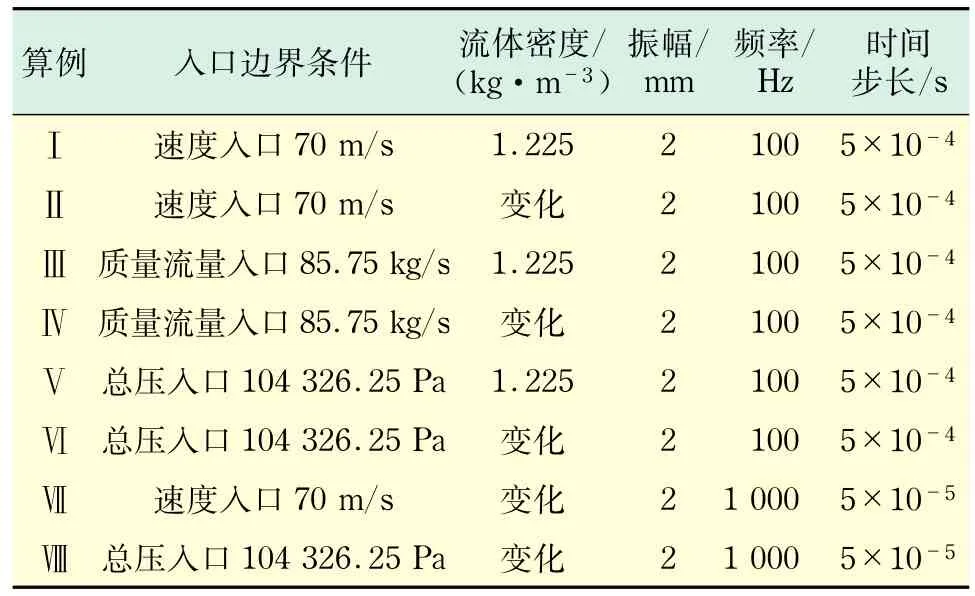
表1 各算例计算条件Tab.1 Boundary condition in each case

2 计算结果与分析

2.1 不可压缩情况入口边界条件的影响

算例Ⅰ,Ⅲ,Ⅴ的入口边界条件不同,其相对静压P分布如图3所示(见下页),可以看出,算例Ⅰ给定速度入口,与算例Ⅲ给定质量流量入口时中轴线上静压分布形态相似,在相同相位下对应的静压值有所不同.算例Ⅴ为给定总压入口,其静压分布明显与算例Ⅰ,Ⅲ不同,呈进口、出口大致对称的形状,这是由于总压入口条件对于入口的流速没有限制.因此,壁面的局部振动对整个管道的静压分布都有影响,且管内流体静压值的波动相对于算例Ⅰ,Ⅲ中管内流体静压值的波动更低.

图4(见下页)为算例Ⅰ,Ⅲ,Ⅴ的中轴线速度分布图,算例Ⅰ,Ⅲ振动壁面上游处中轴线速度基本不变,这是由入口边界条件限制的;振动壁面下游变化规律也基本类似.而采用总压入口的算例Ⅴ,由于对入口速度没有限制,因此,振动壁面对其上、下游都有影响,且速度波动呈左右对称的趋势.当管道向内挤压(0～90°,270～360°),管内上游速度相对于壁面不振动状态时更低,下游速度相对增大;反之,管道向外扩张(90～270°),管内上游速度相对于壁面不振动状态时更大,下游速度减小.同样,管道处于原型时(180°,360°),中轴线MN上速度变化幅度达到极值.

采用总压入口时的静压云图如下页图5所示,

振动壁面下游的流体静压变化规律,与采用速度入口(图6)及质量流量入口时类似;而振动壁面上游的静压变化与下游的变化规律相反,即云图呈左右对称状.当振动相位使管道处于向内压缩时(0～180°),振动处上游段流体相对管道平衡状态时更难流入管道,由于流体惯性有使其保持现有状态的作用,产生正压梯度推动流体流入,所以,振动处上游段静压由左向右递减;振动处下游段流体相对管道平衡状态时更易从出口流出,由于惯性产生逆压梯度阻碍流体向出口流出,因此,下游段静压由左向右递增.

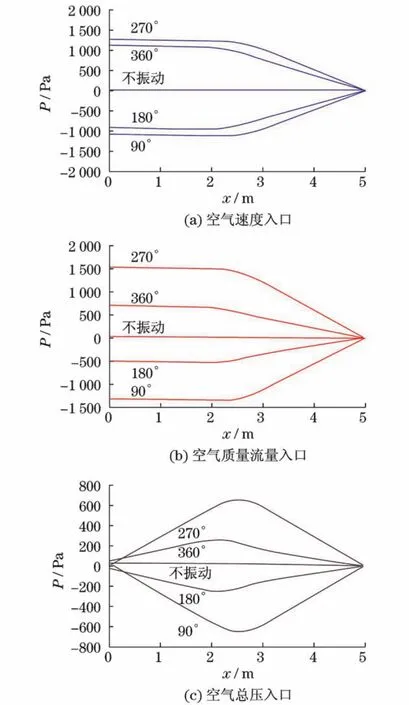
图3 算例Ⅰ,Ⅲ,Ⅴ中轴线相对静压分布Fig.3 Static pressure on the MN of caseⅠ,Ⅲ,Ⅴ

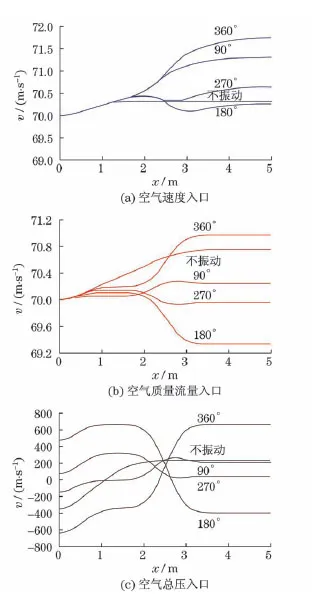
图4 算例Ⅰ,Ⅲ,Ⅴ中轴线速度分布Fig.4 Velocity on the MN of caseⅠ,Ⅲ,Ⅴ

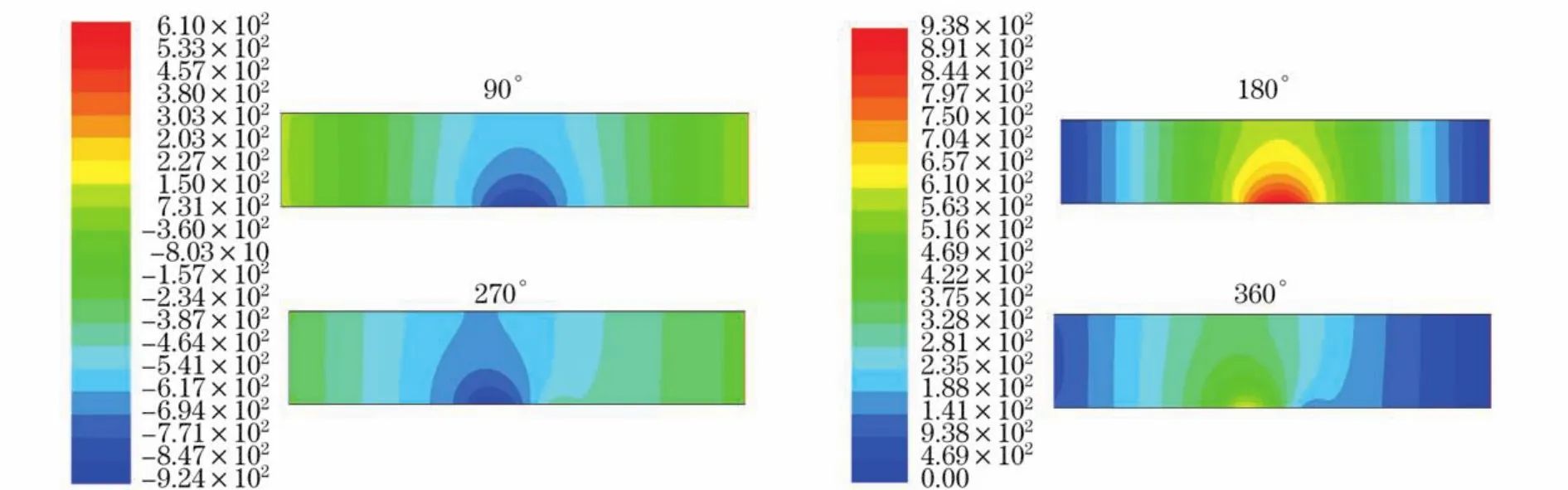
图5 算例Ⅴ90°,180°,270°,360°相位静压云图Fig.5 Static pressure contours of caseⅤin 90°,180°,270°,360°

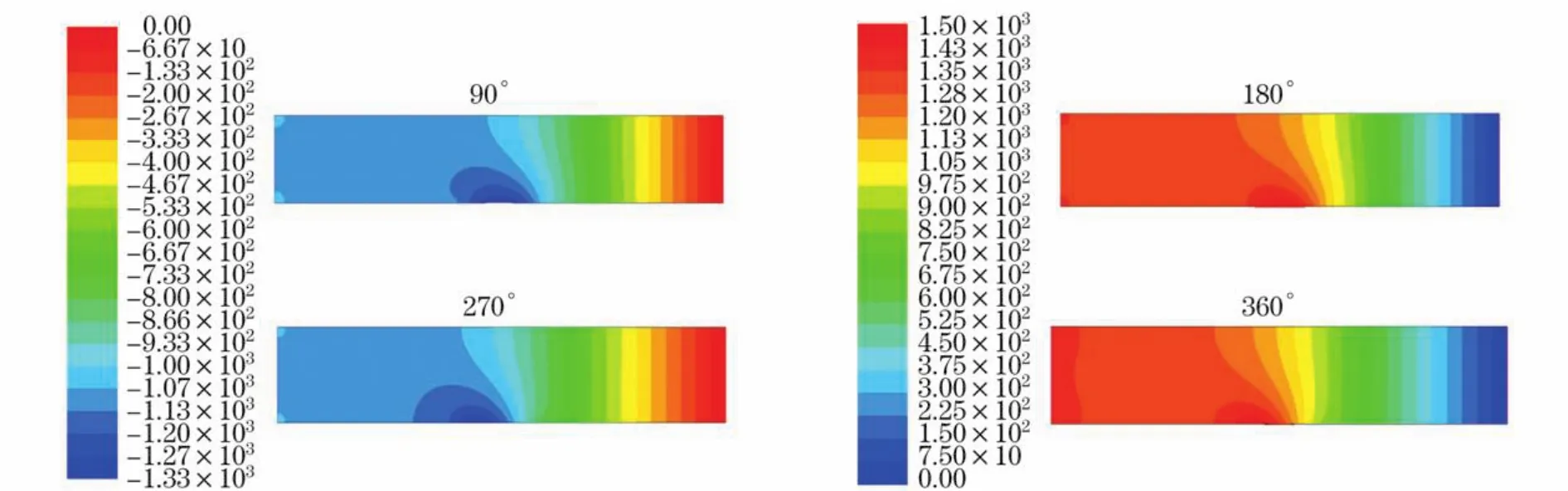
图6 算例Ⅰ90°,180°,270°,360°相位静压云图Fig.6 Static pressure contours of caseⅠin 90°,180°,270°,360°

综上所述,在不可压缩计算条件下,给定速度入口与质量流量入口时管道内物理量变化趋势大致相同,且前者所得物理量波动较小.给定总压入口条件时,振动壁面会同时影响管道上、下游物理量.

2.2 可压缩计算情况入口边界条件的影响

2.2.1 低频振动状况下

算例Ⅱ,Ⅳ,Ⅵ采用空气可压缩气体模型计算,管道入口温度取300 K,管道出口边界给定静压P1=101 325 Pa,采用理想气体状态方程,管道壁面为绝热.由图7可知,在振动壁面的作用下,可压缩流体中的静压和速度分布规律与不可压缩流体相比有很大的不同,静压和速度都呈波动状分布,这是因为在可压缩流体中压力波的传播速度是有限的.静压分布在振动处于90°与270°, 180°与360°相位时基本互相对称.由图7-9(见下页)中轴线相对静压分布可见,可压缩计算体现了压力波的传递过程,且马赫数分布随之变化.由静压云图(下页图10)可知,静压分布更不均匀,而且振动区域上、下游的静压分布明显不同,这与不可压缩流动现象有较大区别.

同时在可压缩流动模型的低频计算情况下,3种边界条件对于中轴线MN相对静压及马赫数的影响比不可压缩情况下的小(图11-13),这是由于压力波的传播速度有限,入口边界条件对于整个流场的影响比不可压缩情况下的限制少.采用速度与质量流量入口边界条件时流场的入口边界、纵轴线、中轴线上的相对静压几乎完全一致,而采用总压入口边界条件,由于入口总压已经给定,因此,在上述3条监控线上的物理量与另两种边界条件的仍有区别,相对采用速度、质量流量入口时的物理量波动更小,这点与采用不可压缩流动模型进行计算时的结果是一致的.

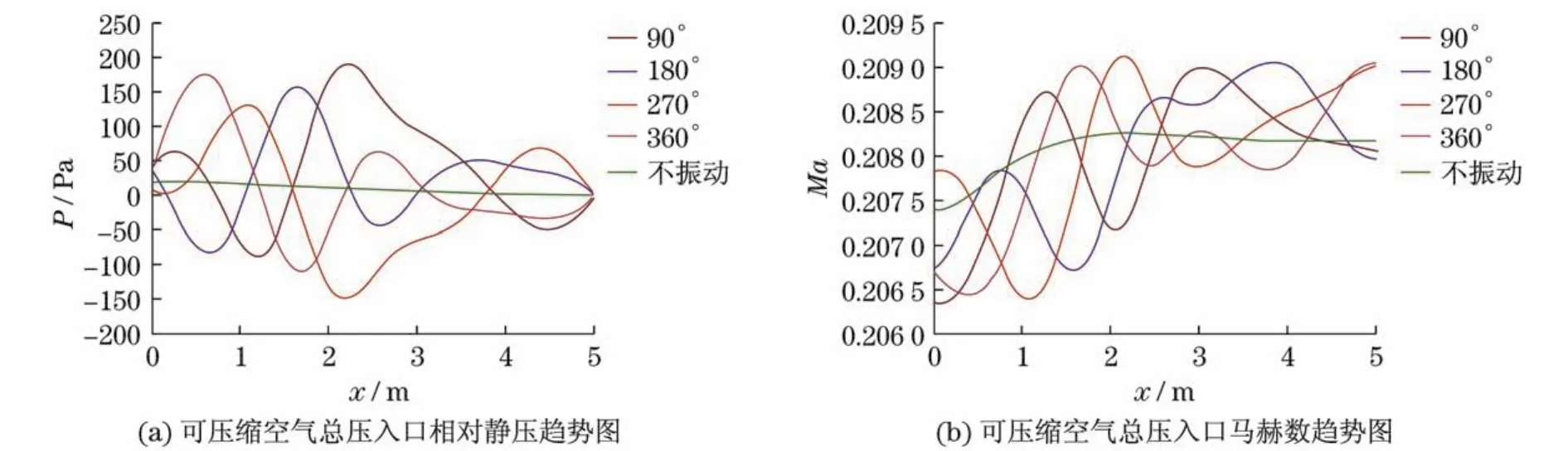
图7 算例Ⅱ中轴线相对静压、马赫数分布Fig.7 Static pressure&Mach number on the MN of caseⅡ

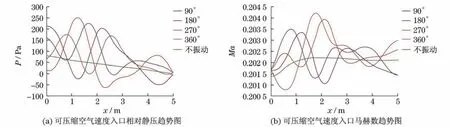
图8 算例Ⅳ中轴线相对静压、马赫数分布Fig.8 Static pressure&Mach number on the MN of caseⅣ

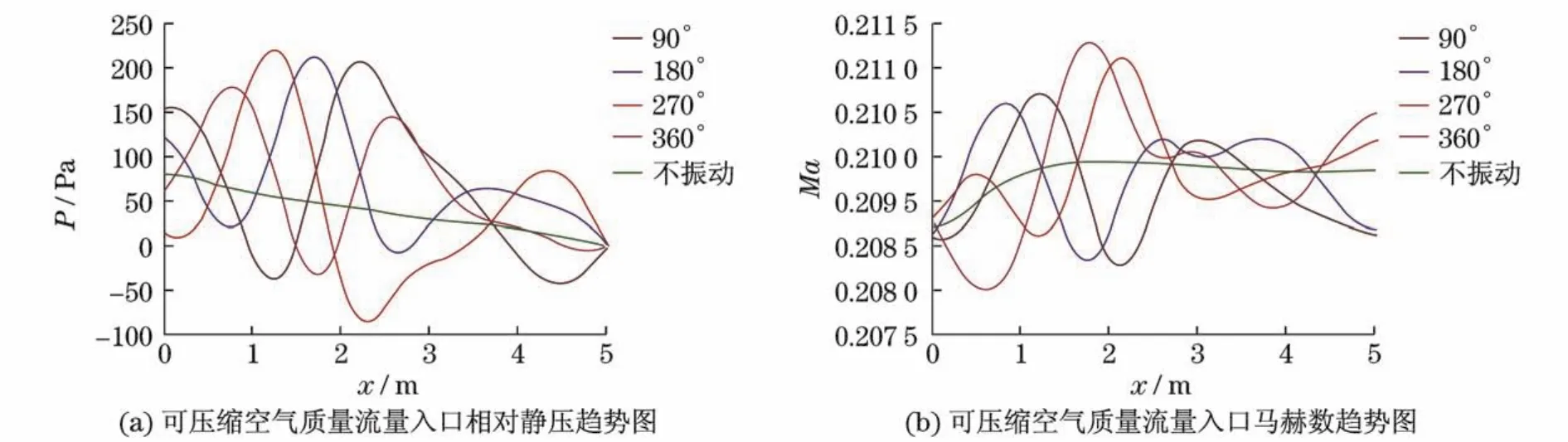
图9 算例Ⅵ中轴线相对静压、马赫数分布Fig.9 Static pressure&Mach number on the MN of caseⅥ

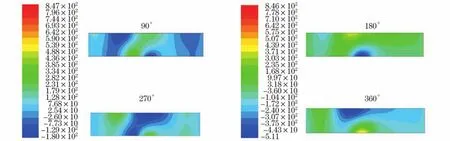
图10 算例Ⅱ90°,180°,270°,360°相位静压云图Fig.10 Static pressure contours of caseⅡin 90°,180°,270°,360°

采用可压缩流体模型计算时,尽管管道进口Ma=0.2,但其压力和速度分布完全不同于不可压缩流动模型.因此,在振动壁面的气体流动计算中,不可以采用不可压缩气体模型进行简化计算,而应该采用可压缩气体模型.

2.2.2 高频振动状况下

在低频振动计算情况下,虽然3种边界条件对于流场的影响已趋于类似,但采用压力入口时仍与采用速度入口及质量流量入口有区别(图11-13).算例Ⅶ,Ⅷ是振动频率为1 000 Hz的高频振动计算.计算结果表明,高频振动情况下,采用速度入口边界时,流场相对静压与采用压力入口边界时相差不大(图14-16).而由于上、下壁面的黏性作用,在附面层区域,采用速度入口边界时的入口段相对静压分布图与采用压力入口边界时的有较大不同,而主流区域大致相同(图14).另外,在纵轴线GH相对静压分布图15中,两者仅在靠近振动壁面附近时有细微差别,采用速度入口边界的壁面处相对静压值较采用压力入口边界的壁面处相对静压值小约420 Pa,同样是由于压力入口边界在入口段忽略了边界层所导致的.在图16中,可见速度入口边界条件与压力入口边界条件在中轴线MN的静压分布图中区别不大.

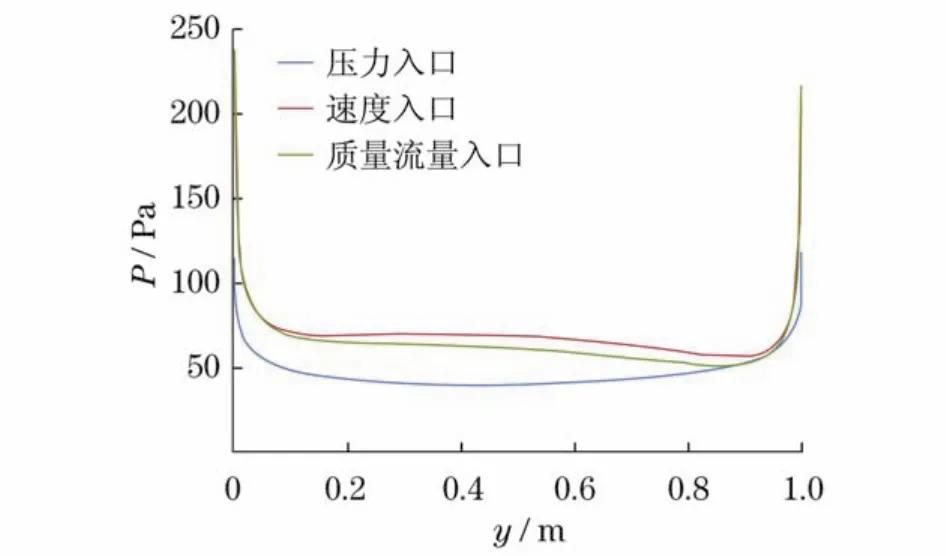
图11 低频振动工况下不同入口边界条件时入口边界AB静压分布Fig.11 Static pressure on the inlet boundary AB of different cases in low frequency circumstance

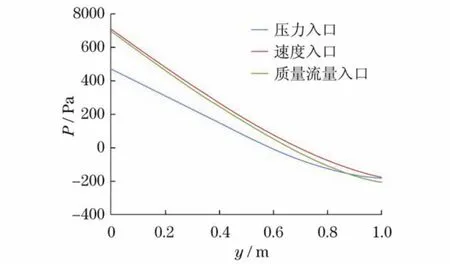
图12 低频振动工况下不同入口边界条件时纵轴线GH相对静压分布Fig.12 Static pressure on the longitudinal axial line GH of different cases in low frequency circumstance

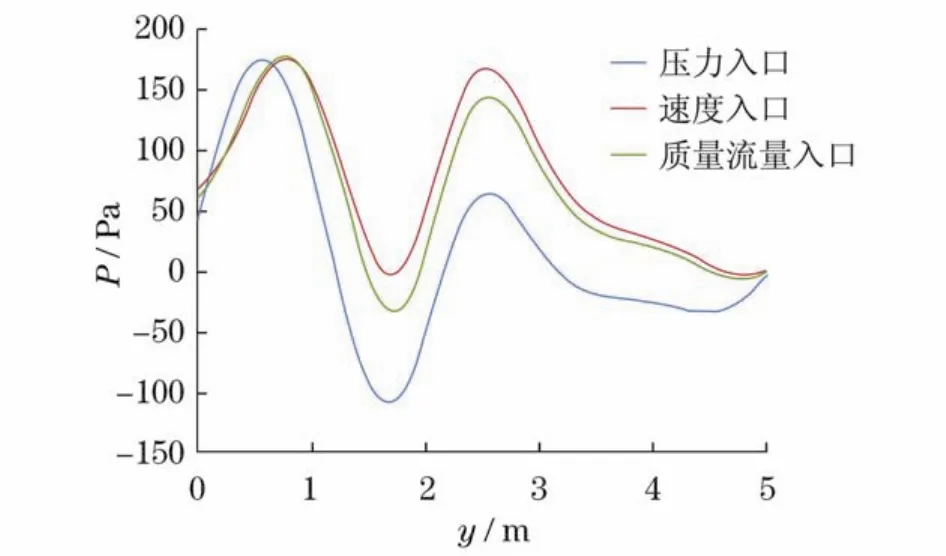
图13 低频振动工况下不同入口边界条件中轴线MN相对静压分布Fig.13 Static pressure on the MN of different cases in low frequency circumstance

因此,在高频小幅振动的可压缩计算情况下,入口边界条件对于振动处流场的影响很小.在相对平缓、充分的入口段条件下,仍然可以采用常规模拟叶片绕流时的速度入口边界条件,它与压力入口边界条件的计算结果相差不大.

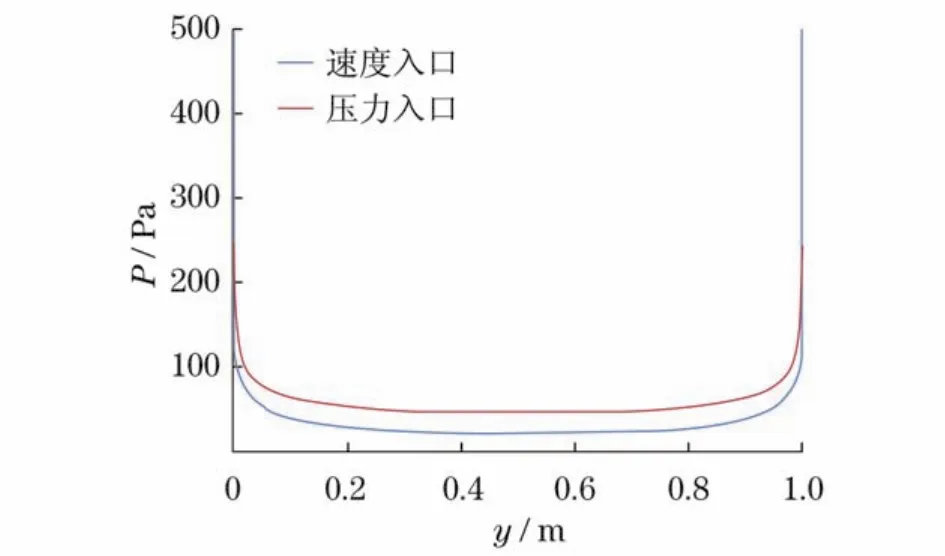
图14 高频振动工况下不同入口边界条件时入口边界AB相对静压分布Fig.14 Static pressure on the inlet boundary AB of different cases in high frequency circumstance

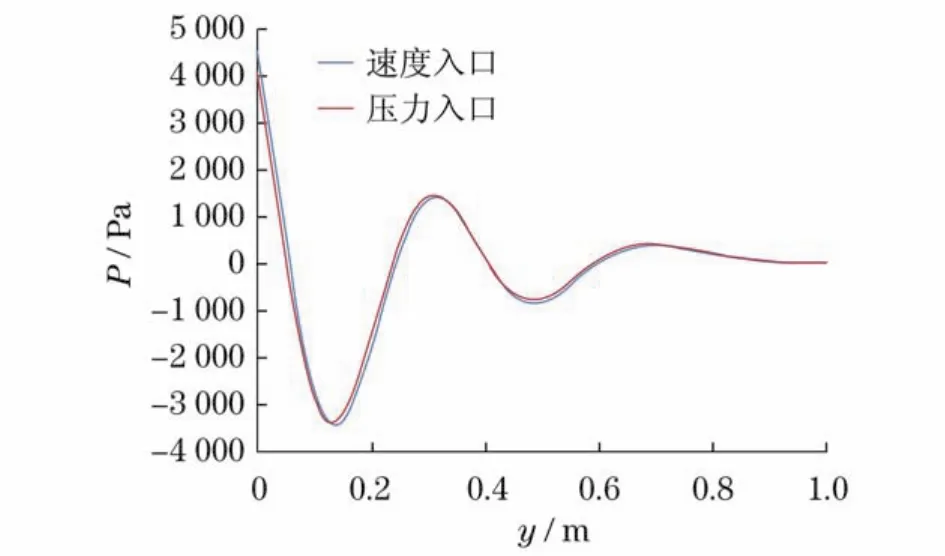
图15 高频振动工况下不同入口边界条件时纵轴线GH相对静压分布图Fig.15 Static pressure on the longitudinal axial line GH of different cases in high frequency circumstance

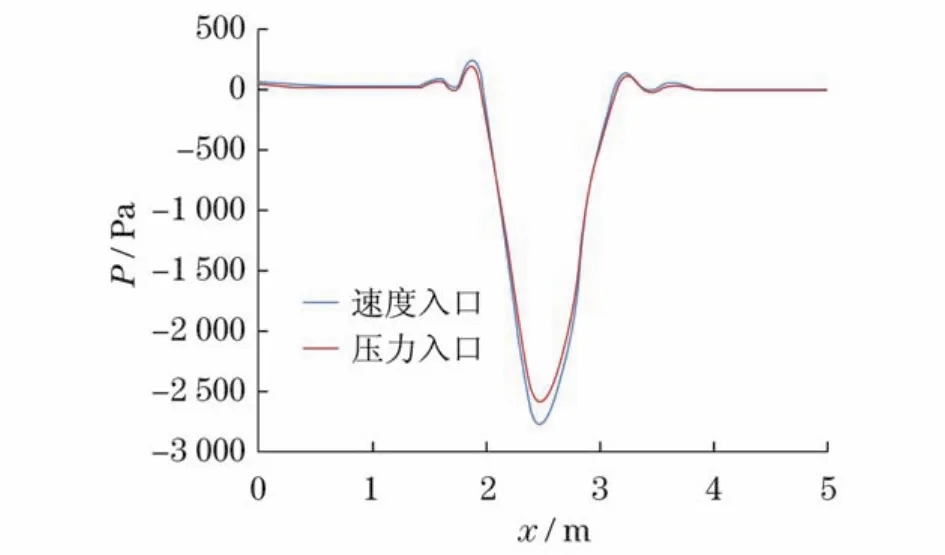
图16 高频振动工况下不同入口边界条件中轴线MN相对静压分布图Fig.16 Static pressure on the MN of different cases in high frequency circumstance

3 结 论

综合以上8个壁面局部振动二维管道算例,得到以下结论:

a.采用不可压缩计算模型时,给定进口速度和给定进口质量流量这两种边界条件对计算结果的影响趋势基本一致,数值有所差异.在振动区域的上游,速度沿中轴线变化不大,静压沿中轴线保持为常数,但该常数随振动相位变化;在振动区域的下游,静压逐步过渡到给定的出口静压值,速度随振动相位变化.采用总压入口条件时,在振动区域的上游,速度随振动相位而变化.进口静压基本不变,静压在管道内的分布随相位变化.

b.采用可压缩计算模型时,静压和速度都呈波动状分布,这是因为在可压缩流体中压力波的传播速度是有限的.相对于不可压缩计算模型情况,采用可压缩计算模型时不同的入口边界条件对流场影响差异小得多.同时,随着振动频率上升,不同的入口边界条件对于流场的影响越来越小.由于基于密度的可压缩计算,低马赫数确实会产生刚性问题,相关系数无限大,导致无法收敛,已经有许多文献作出讨论与设想[12-13],本文的重点是研究振动对流场的影响,这类数值模拟方法本身带来的缺陷就不讨论了.

c.采用可压缩流体模型计算时,尽管管道进口Ma=0.2,但其压力和速度分布完全不同于不可压缩流动模型,因此,在振动壁面的气体流动计算中,不可以采用不可压缩气体模型进行简化计算,而应该采用可压缩气体模型.

[1] 欧阳德,孔瑞莲,宋兆泓,等.带冠和冷却小孔涡轮叶片振动特性分析[J].航空动力学报,1997,12(3): 235-238.

[2] 林垲,高庆,黄维娜.Ⅰ级涡轮叶片振动特性研究[J].燃气涡轮试验与研究,2002,15(3):28-32.

[3] Fan YC,Ju M S,Tsuei Y G.Experimental study on vibration of a rotating blade[J].Journal of Engineering for Gas Turbines and Power,1994,116 (3):672-677.

[4] Wu C M,Tian R,Chen Y Y.Turbine blade design based on optimal vibration performance[J].Journal of Engineering Thermophysics,2008,29(11):1857-1860.

[5] 林宗虎.强化传热及其工程应用[M].北京:机械工业出版社,1987:105-114.

[6] 程林.换热器内流体诱发振动[M].北京:科学出版社,1995:39-42.

[7] 过增元.场协同原理与强化传热新技术[M].北京:中国电力出版社,2004.

[8] 崔天福,丁晓红,侯丽园.基于密度法的传热结构拓扑优化设计[J].上海理工大学学报,2014,36(6): 548-555.

[9] 宿艳彩,葛培琪,闫柯,等.流体绕流不同方向振动圆柱换热特性数值分析[J].振动与冲击,2011,30(10): 221-223.

[10] 裘进浩,李大伟,聂瑞,等.增加翼型升力的局部振动流动控制技术[J].南京航空航天大学学报,2012,44 (5):638-644.

[11] Anderson J D.计算流体力学基础及其应用[M].吴颂平,译.北京:机械工业出版社,2007:15-30.

[12] 王涛.适用于可压缩和不可压缩流动的NS方程预处理数值解法[J].水动力学研究与进展,2009,24(4): 519-526.

[13] 曹宁,吴颂平.低速流预处理Roe格式中的数值黏性[J].北京航空航天大学学报,2010,36(8):904-908.

(编辑:石 瑛)

Two-Dimensional Flow Analysis of Locally Vibrating Wall Tube

XUChenghua, WANGHongguang, ZHUZhiwen
(Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

By solving the two dimensional RANS Navier-Stokes equations,the partially vibrating wall in the two-dimensional tube flow field was simulated and the impact of different boundary conditions in the calculation of incompressible and compressible situations on the partially vibrating wall was analysed.The results show that:compared with the total pressure inlet condition,the velocity inlet and mass flow inlet conditions have less restriction on the flow in the case of incompressible calculation,so,the wall vibration can affect the up and down stream flow parameters simultancously.Moreover,even if the Mach number Ma＜0.3,the compressible fluid flow phenomena are completely different from those under the incompressible fluid calculation conditions.Meanwhile,compared with low-frequency vibration conditions,the influence of boundary conditions on the calculation results of high-frequency vibrations is even smaller.Therefore,to simulate the actual gas turbine with a small high-frequency vibrating cascade,in the calculation the compressibility of fluid should be taken into account.Under relatively gentle and sufficient inlet conditions,a conventional analogic velocity inlet in the calculation of the flow around the blade can still be used.

pipeline flow;wall vibration;boundary conditions;compressible flow

管道流动;壁面振动;边界条件;可压缩流动

TK 124

A

1007-6735(2015)05-0450-07

10.13255/j.cnki.jusst.2015.05.007

2014-09-16

高等学校博士学科点专项科研基金联合资助课题(20123120110009)

许成骅(1991-),男,硕士研究生.研究方向:燃气轮机叶片冷却技术.E-mail:xchxch_turbine@163.com

王宏光(1962-),男,教授.研究方向:流体机械、动力机械.E-mail:1352048859@qq.com