0709号台风影响下粤东后江湾海滩地形动力过程研究

于吉涛，丁圆婷，程璜鑫，陈子燊

(1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000; 2.中国地质大学(武汉) 环境学院，湖北 武汉 430074;3.中国地质大学(武汉)艺术与传媒学院，湖北 武汉 430074；4.中山大学 地理科学与规划学院，广东 广州 510275)

0709号台风影响下粤东后江湾海滩地形动力过程研究

于吉涛1，2，丁圆婷1，程璜鑫3，陈子燊4*

(1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000; 2.中国地质大学(武汉) 环境学院，湖北 武汉 430074;3.中国地质大学(武汉)艺术与传媒学院，湖北 武汉 430074；4.中山大学 地理科学与规划学院，广东 广州 510275)

基于0709号台风“圣帕”影响下粤东后江湾的现场实测海滩前滨地形资料和水动力、风等资料，采用典型相关分析方法识别了台风影响下海滩前滨地形不同的变化过程，揭示了这些不同变化过程的主要控制因子，并尝试给出了物理解释。研究结果表明：(1)台风影响下海滩前滨地形的主要变化过程是水上滩肩被破坏—水下岸坡略有堆积—水下沙坝泥沙向海搬运，控制这一过程的主要动力因子是风速东向量、最大波高和碎波尺度参数；(2)海滩前滨地形的次要变化过程是海滩前滨泥沙向海搬运而形成水下沙坝，控制这一过程的主要动力因子是最大波周期和海滩地下水位；(3)海滩前滨地形也表现出前滨上部地带堆积、下部侵蚀的变化过程，控制这一过程的主要动力因子是沿岸流、海滩地下水位和最大波高。这些研究结果进一步揭示了台风影响下海滩前滨地形动力过程是由多个不同的地形-动力过程耦合作用而组成。

地形动力过程；海滩；台风；典型相关分析

1 引言

海滩演变涉及波浪、潮汐、风等动力因素在不同时空尺度下的地形动力过程。因此，海滩地形与动力是泥沙粒度、破波波候(包括波高和周期)、潮差和主要地形单元的函数[1]。偶尔发生的风暴、飓风和热带气旋形成的极端事件在短时间内也会对海滩地形动力过程产生巨大影响，导致严重的侵蚀、波浪越顶和海滩系统的不稳定，产生灾难性的后果[2—6]。通常，具有较大波高的风暴能够造成更大的危害，而其他风暴特征如风暴持续时间、方向、峰波周期和水位(潮汐和浪涌)也发挥了重要的作用。许多研究指出，海滩对风暴的响应是海滩类型和风暴特征的函数[7]。

常况下，近岸波浪与海滩剖面响应之间的关系本身就是一个高度复杂的现象，因为其中包含了不同时空尺度下不同的过程[8—9]。除非在明确的情况下只有几个过程控制海滩剖面的响应(如物理模型)，否则很难用简单的、确定性的方程或模型来研究波浪与海滩剖面之间的关系[10]，这就需要借助更高级的统计模型，以识别数据中的模式并将其与物理过程联系起来。有关研究人员使用典型相关分析(Canonical Correlation Analysis，CCA)，研究了海滩剖面与波浪之间的关系，得到了较好的结果[10—12]。但是目前，研究海滩剖面变化与波浪之间的关系只是取得了有限的进步，究其原因是在大部分研究中缺乏时间上密集的同步海滩地形和近岸波浪数据[12—13]，进而限制了CCA法的应用。

在风暴(台风)影响下，海滩地形与动力因子之间的关系更加复杂，近岸数据的获取更加困难，国内外研究中鲜见风暴(台风)作用下海滩地形与波浪、潮汐、风等多个动力因素同步观测数据。本文将基于0709号台风影响下粤东后江湾现场实测海滩前滨地形数据和波浪、潮汐、风等动力数据，拓展CCA法的应用，将常况下海滩剖面与近岸波浪之间的关系研究拓展至极端波况下海滩剖面与近岸波浪、潮汐、风等多个动力因素之间的关系研究，识别台风影响下海滩前滨地形不同的变化过程；通过研究海滩前滨剖面不同部位与近岸动力因子之间的关系，揭示海滩前滨地形变化不同变化过程的主要控制因子，并尝试给出物理解释，研究成果将有助于认识、理解华南砂质海滩时空演变特征与侵蚀机制。

2 研究区概况与台风情况

研究区位于粤东碣石湾西南的岬间海湾——后江湾(图1)，湾口向东偏南方向开敞，海岸地形由海湾西南的遮浪角和东北部的施公寮两个基岩岬角和连接两者的海成沙堤构成。该海湾主要位于潮间带的前滨区，岸滩宽约50～60 m，滩肩、滩角与陡滩面是前滨地形的主要特征。据当地海洋站长期观测结果，湾口外开阔海区平均波高约1.3 m，平均周期4.6 s；风速、风向及波向变化都较大。海区潮汐为不正规日潮混合潮类型，平均潮差小于1 m，属波控弱潮海岸[14]。

0709号台风“圣帕”是2007年最强的一个台风，也是近年来强度最强的台风之一，并为台湾、福建及浙江带来严重损失。其形成过程与路径(图2)为：一个低压区于2007年8月12日在马尼拉以东约1 600 km增强为一个热带低气压，初时向西南偏西移动；8月13日凌晨增强为热带风暴，日本气象厅将其命名为“圣帕”，当晚迅速增强为强热带风暴；8月14日进一步增强为台风。“圣帕”增强为台风后于8月15日转向西北偏西移动，8月16日下午转向西北偏北移动。台风“圣帕”于当晚达到颠峰程度，每小时风速高达200 km，同时“圣帕”亦出现拥有双重眼壁并进一步逼近台湾。“圣帕”于2007年8月18日凌晨减弱为强台风，5时40分前后在中国台湾花莲秀姑峦溪口附近沿海登陆。“圣帕”穿越台湾及台湾海峡，并于8月19日凌晨减弱为强热带风暴。当日早上在福建泉州市登陆并减弱为热带风暴，当晚进一步减弱为热带低气压，8月20日清晨减弱为一个低压区。“圣帕”台风对本文研究区的影响时间为2007年8月14-17日。

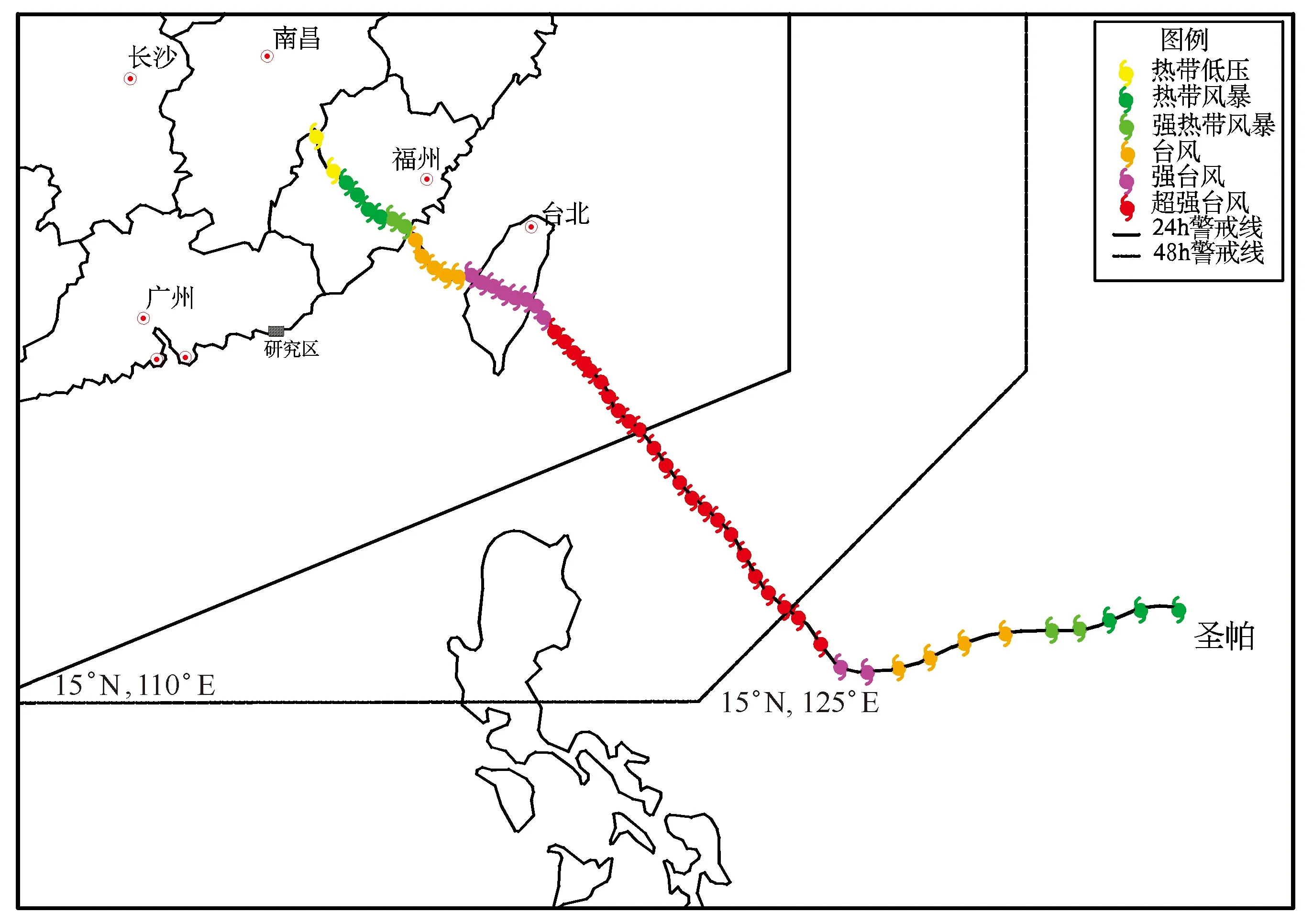
图2 台风“圣帕”路径图Fig.2 The typhoon “Sepat” track

3 数据与方法

3.1 现场数据

3.1.1 海滩剖面数据

现场观测自2007年8月12日14时至21日18时，共221 h。在海滩上布设两条观测剖面A与剖面B(见图1)。剖面A布设7根铁桩(a1～a7)，剖面B布设8根铁桩(b1～b8)，铁桩间距为4 m，向陆侧大致到高潮时波浪最大上冲处，向海侧至平均水下约1 m处，包括了整个海滩前滨区域。剖面A靠岸一侧有人工石堆拦沙堤。对剖面上各桩点高度变化进行昼夜连续观测，时间间隔为1 h，剖面A与剖面B分别连续测量221次，剖面形态如图3所示。由剖面A与剖面B的布设位置可知(见图1)，剖面A的地形变化除了遭受入射波作用之外，还受到其右侧人工石堆拦沙堤的影响。本文关注的是自然条件下海滩前滨地形的演变，故选用剖面B所观测的剖面数据。

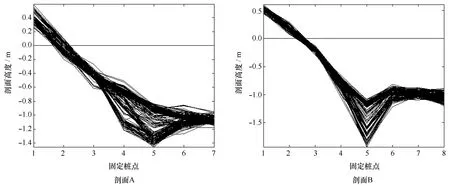
图3 实测剖面A、B的形态图Fig.3 Shapes of the observed profiles A and B

3.1.2 近岸动力数据与预处理

在现场剖面观测期间，同时在水下沙坝海侧斜坡和岸侧的凹槽内(见图1)分别安置一部美国InterOcean公司生产的S4ADW型测波仪采集波浪数据，采样频率为2 Hz。对观测期间的波浪数据进行处理，得到221 h逐时的最大波高H和最大波周期T(图4)；并于剖面B的右侧挖一探井，井底安置DIK-610A-CI水位计记录海滩地下水位，采样间隔为1 min，海滩地下水位的变化将指示潮汐的作用过程。对观测期间的海滩地下水位数据进行处理，得到221 h逐时的地下水位数据ζ(图4)；现场同步获取的风速的数据W(图4)，对221 h风速的数据进行预处理，分解为风速东分量Wu和风速北分量Wv(图5)。风速东分量Wu指示近岸沿岸流的作用过程，风速北分量Wv指示近岸离岸流的作用过程。

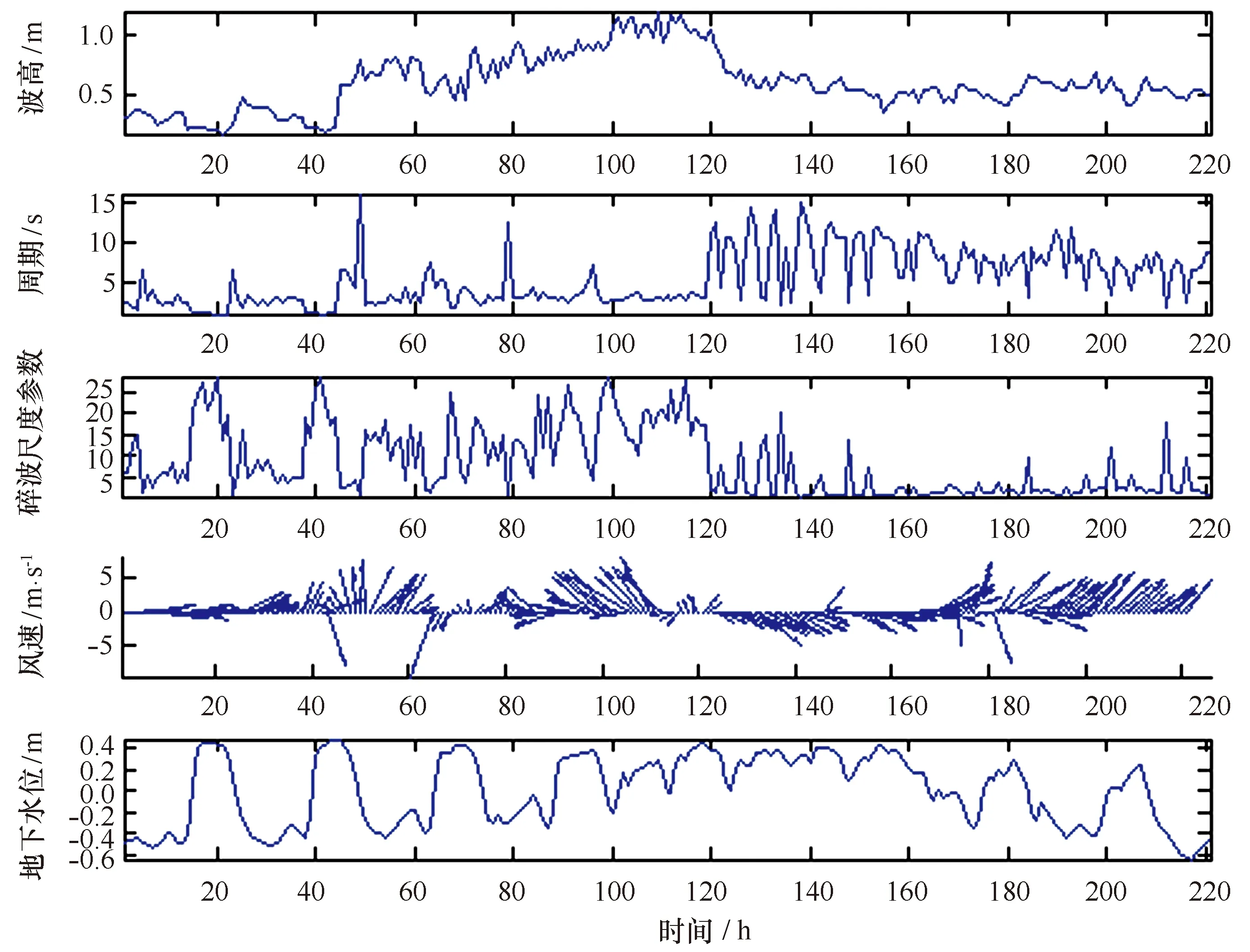
图4 实测的波高、周期、碎波尺度参数、风速、风向、海滩地下水位过程Fig.4 Observed field wave heights，periods，surf scaling parameters，wind speed，wind direction and beach waver tables

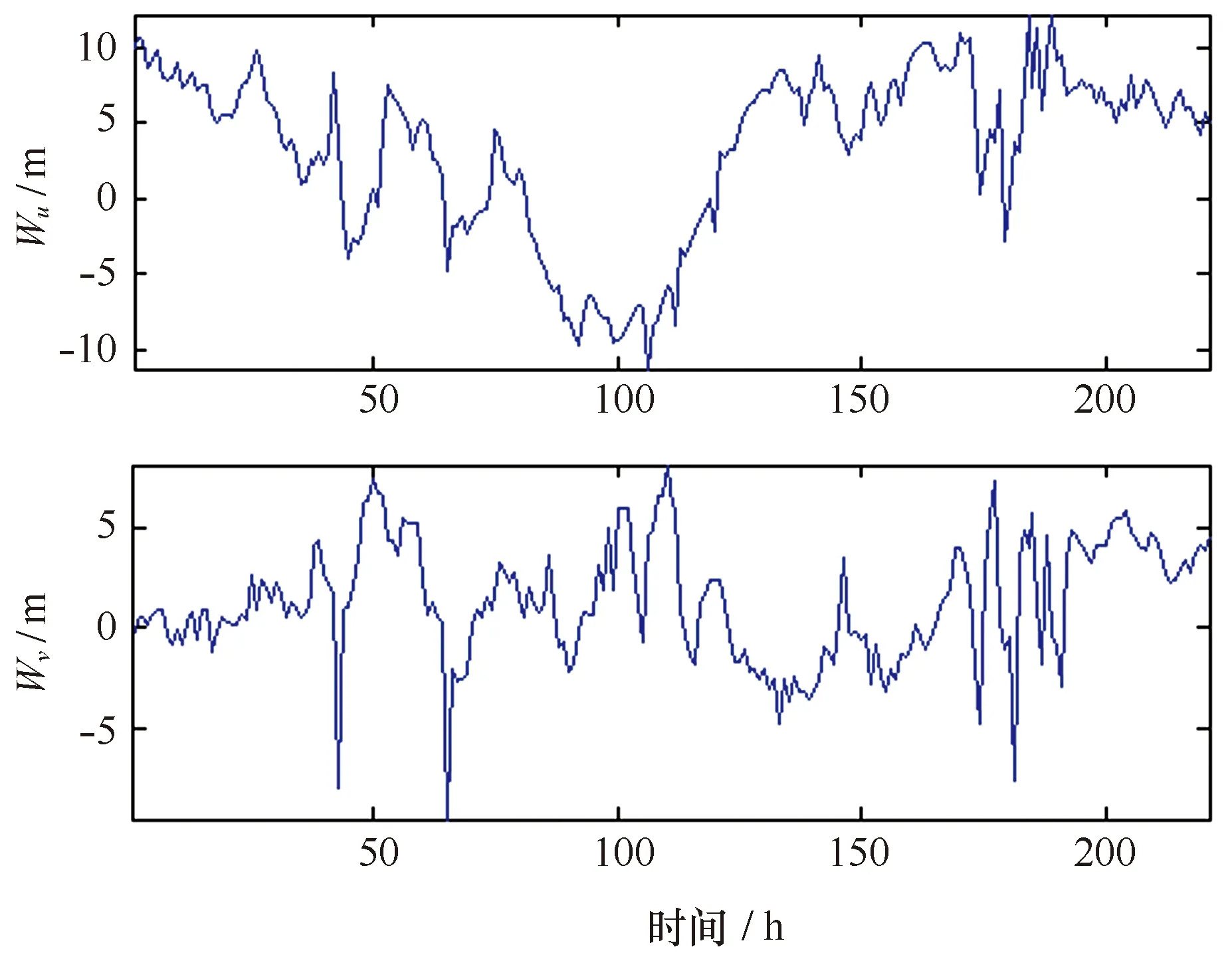
图5 221 h连续时序风速东分量Wu和风速北分量WvFig.5 Eastern component Wu and northern component Wv of the wind speed within 221 hours

3.1.3 碎波尺度参数

Guza和Inman认为波能对海滩作用的强度可通过海滩反射性与碎波类型来表征，通过实验室和理论调查，提出了描述碎波带破波类型的参数——碎波尺度参数(surf scalling parameter)[15]：

(1)

式中，ai为破波振幅，ω为入射波频率(ω=2π/T，T为周期)，g为重力加速度，β为海滩坡度。根据这一公式，破波类型可被划分为激破波(εs<2.5)、塌破波和卷破波(2.5<εs<20)和溢破波(εs>20)。Wright和Short通过对澳大利亚不同海滩和碎波带环境进行了现场研究，将海滩状态与碎波尺度参数联系起来，采用碎波尺度参数来表征海滩对入射波的反射性，判别海滩的水动力特征，识别出海滩状态的两种极端状况：完全消散型和高度反射型。他们提出：反射型海滩(εs<2.5)、中间状态海滩(2.5<εs<20)和消散型海滩(εs>20)[16]。已有的研究指出，消散型海滩更常见于风暴作用下的风浪环境中，波高大、周期短的风暴浪作用于极细砂海滩[17—20]。本文引入这一参数，识别台风作用下海滩类型的变化，通过同步测量的海滩坡度数据与波浪数据，得到221 h逐时的碎波尺度参数εs(见图4)。

3.2 研究方法

典型相关分析是研究两组变量之间相关关系的一种多元统计方法，由Hotelling于1936在社会学中提出[21]。这一方法在海岸演变方面最早的应用是Larson等调查波浪和剖面响应之间的关系研究[10]。随后，Horrillo-Caraballo和Reeve使用CCA法研究了英国南部海岸Christchurch Bay的卵石-沙混合型海滩和美国东海岸北卡罗莱纳州沙质海滩，通过海滩剖面与波高分布之间显著相关性，提出CCA方法可用来预测海滩剖面[12]。另外，Rózyński也使用CCA法研究了多列沿岸沙坝的演变形式和它们之间的相互作用[22]。在目前海岸演变与预测方面依然更多偏重统计方法的背景下，CCA法作为一种高级的统计方法，可以确定两个数据组的主要模式和其中的关系，因此可以更好的揭示海滩演变的过程与主要的控制因子。主要计算过程为：设有变量场X、变量场Y分别由p个空间地形高程点，q个海滩动力因子构成，样本容量为N。对两组要素分别加以标准化处理，然后分别寻找X和Y中诸个变量的线性组合

(2)

(3)

式中，Ui,Vj称作典型变量，要求它们有如下性质：

(1)所有的Ui或Vj之间彼此正交；

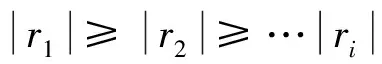
(3)各Ui或Vj的均值都为0，方差都为1。

典型相关分析的优越之处在于分析上述两个线性组合中各项组合系数(可视为该项变量的权重系数)绝对值的大小和正负号可以揭示各项典型变量的物理意义。对所得典型相关系数采用巴特莱特(Bartlett)关于大样本的χ2检验，显著水平取α=0.05，当经χ2检验求得的统计量P小于α值时，该典型变量显著[23]。

本文聚焦于台风影响下海滩前滨剖面地形与近岸动力因子之间的相互关系，那么剖面B的8个固定桩点(b1～b8)为剖面地形高程组x1～x8(X变量组)；基于前文获得的波浪、海滩地下水位、风的数据，首先通过对各波列组的偏度、峰度、波高和周期、入射波频带波高、入射波频带周期、长重力频带波高、长重力频带周期、沿岸流分量、垂岸流分量、波能、波能流、海滩潜水位等近岸动力因子做常态相关分析，最终选取最大波高y1、最大波周期y2、风速东分量y3、风速北分量y4、海滩地下水位y5和海滩碎波尺度参数y66个近岸动力因子，组成海滩动力因子组(Y变量组)；X、Y组样本数N等于221(逐时过程)。

4 结果与分析

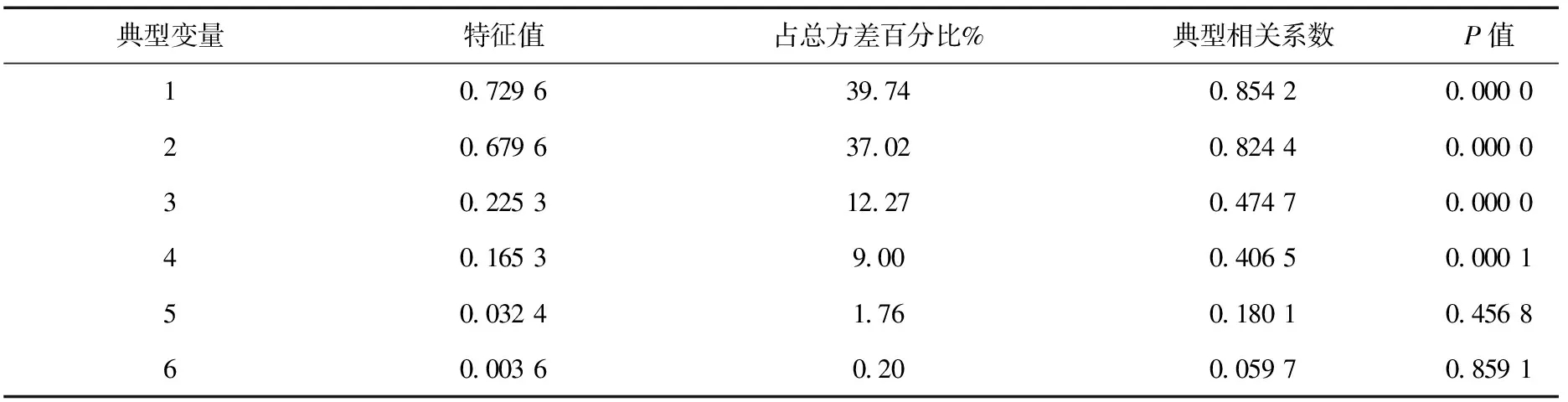
典型相关分析结果如表1和图6。表1显示前4个典型变量累计总方差达到98.04%，统计量P值小于显著水平0.05，属于显著典型变量。从图6也可以看出，前4个典型特征变量所对应的Ui、Vj之间相关系数较强(i=1，2，…，8；j=1，2，…，6)，典型相关系数r1～r4介于0.406 5～0.854 2。结果与具体分析如下：

(1)由表1可得出第1典型变量占总方差的39.74%，U1与V1的典型相关系数r1为0.854 2，说明海滩前滨剖面地形变化与近岸动力因子之间具有高度的相关关系。由表2、表3可知所对应的第1对标准化的典型变量的线性组合为：

U1=-0.873 2x1-0.497 2x2+0.003 7x3+

0.091 7x4+0.175 7x5-0.064 8x6-

0.520 9x7-0.619 3x8，

(4)

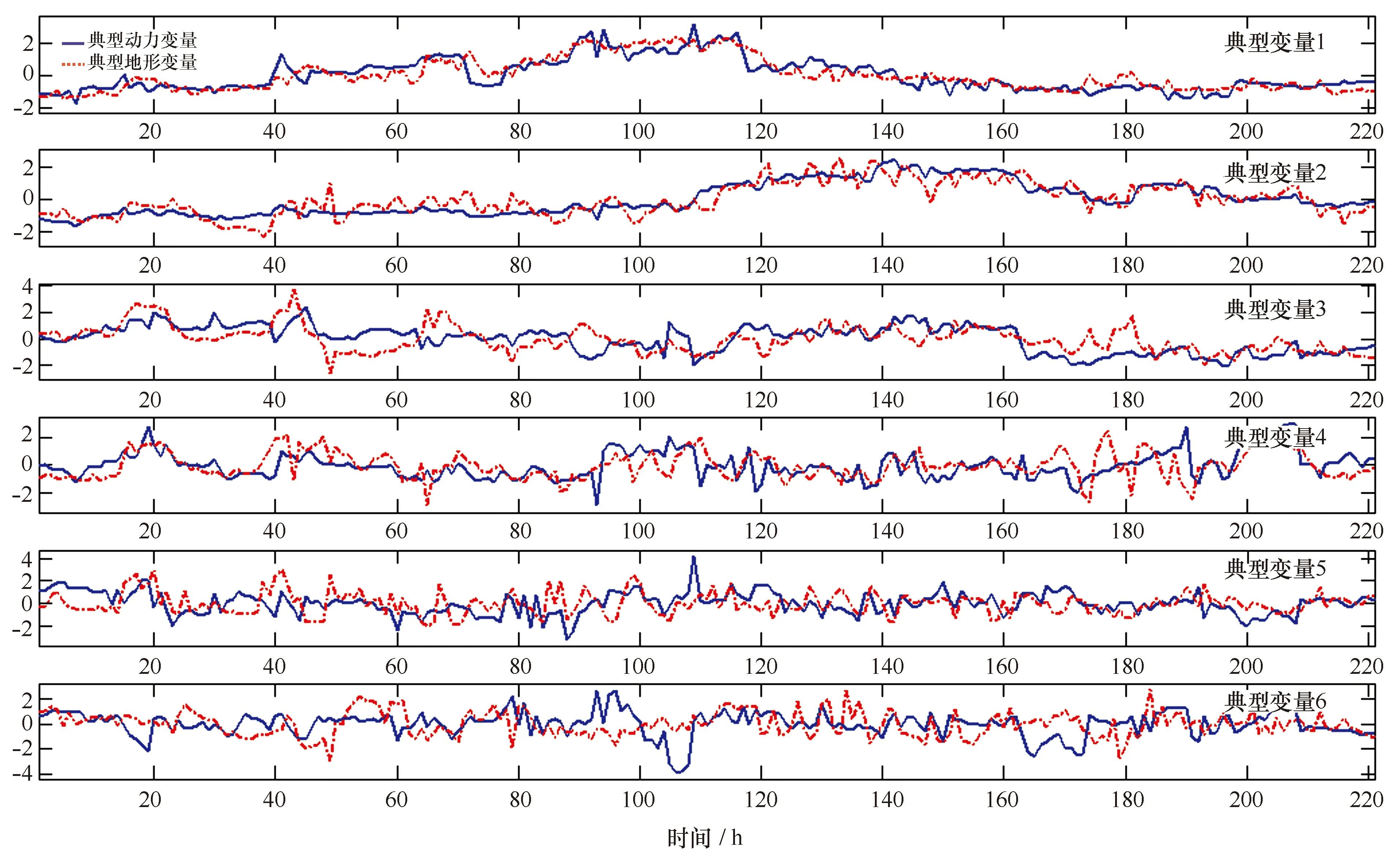
图6 6个典型相关变量时间过程Fig.6 Temporal processes of six canonical correlation variables

表1 6个典型变量的特征值、相关系数和统计P值

Tab.1 Eigenvalues，correlation coefficients and statistic values of six canonical correlation variables

典型变量特征值占总方差百分比%典型相关系数P值10 729639 740 85420 000020 679637 020 82440 000030 225312 270 47470 000040 16539 000 40650 000150 03241 760 18010 456860 00360 200 05970 8591

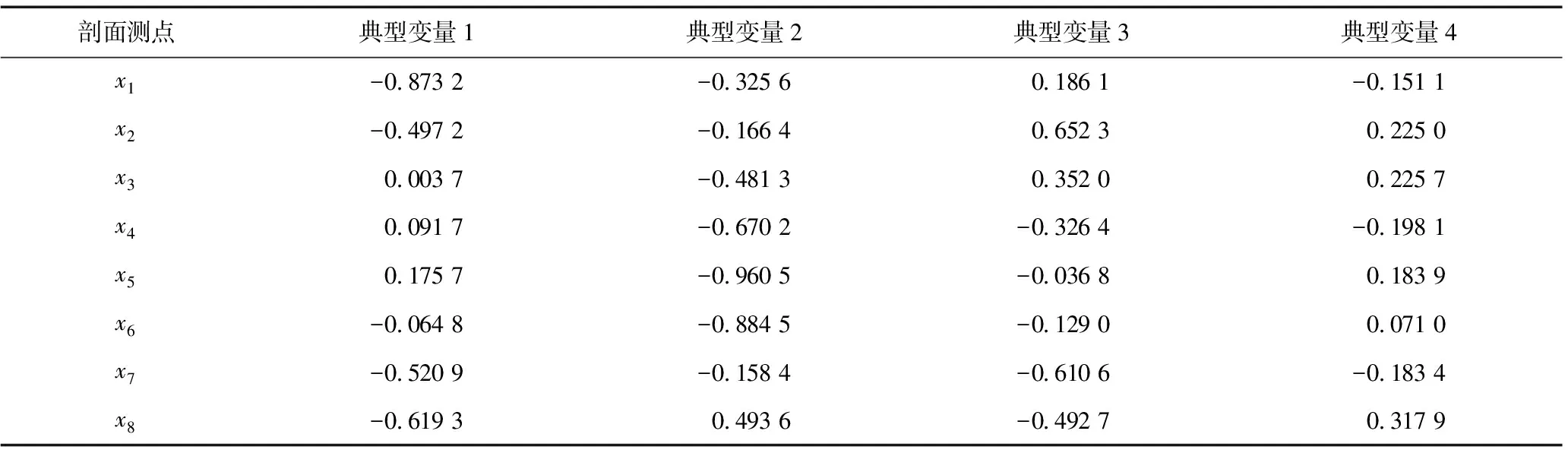
表2 4个显著典型相关变量和8个剖面高程点之间的相关系数

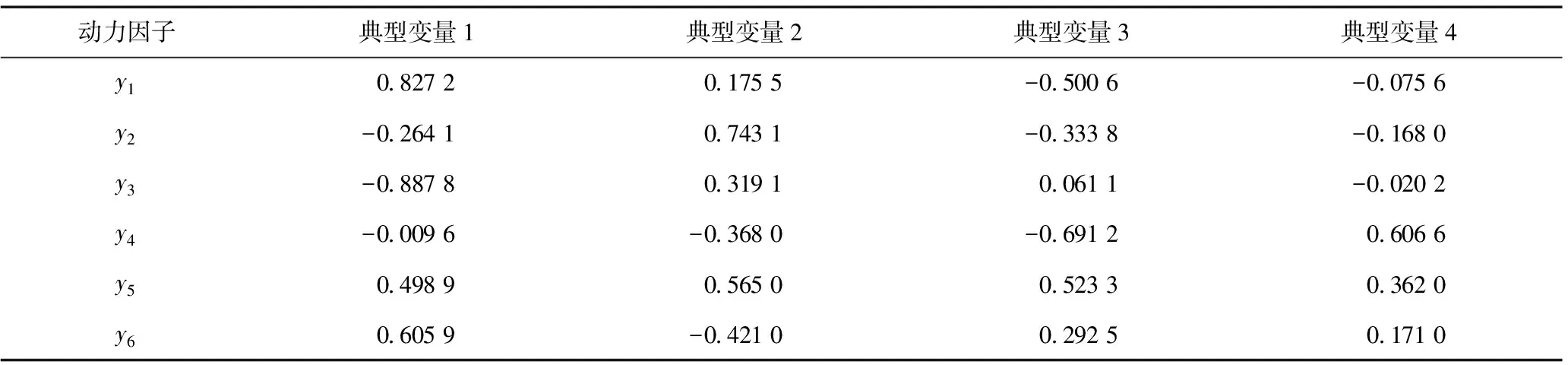
表3 4个显著典型相关变量和6个近岸动力因子之间的相关系数

V1=0.827 2y1-0.264 1y2-0.887 8y3-

0.009 6y4+0.498 9y5+0.605 9y6，

(5)

由式(4)、(5)可知，第1典型变量与桩点b1、b2呈负相关，与桩点b3、b4、b5呈正相关，与桩点b6、b7、b8又呈负相关，对照图3可得出在台风作用下，海滩水上地形(滩肩破坏)发生侵蚀，沿岸坡向水下搬运，使岸坡区域略有堆积，从水上搬运的泥沙将在岸坡下部形成水下沙坝，并向海侧搬运而发生侵蚀，这是海滩前滨剖面地形变化的主要模式。整个过程体现了台风作用下海滩前滨地带的侵蚀过程，反之当台风过后，整个地带又会经历相反的过程向陆搬运泥沙而重塑海滩。其中，第1典型变量与海滩前滨剖面桩点b1、b8关系更加紧密(相关系数分别为-0.873 2和-0.619 3)，都呈负相关关系，体现了台风作用下对这两个地带的扰动更强，共同指示了台风作用下海滩遭受侵蚀的事实。

第1典型变量与近岸动力因子最大波高y1、海滩地下水位y5和海滩碎波尺度参数y6呈正相关，与最大波周期y2、风速东分量y3和风速北分量y4呈负相关。其中相关关系显著的3个近岸动力因子分别为风速东向量y3、最大波高y1、碎波尺度参数y6，说明这3个动力因子对海滩前滨剖面地形变化主要模式的控制。第1典型变量与风速东向量y3关系最密切，相关系数为-0.887 8，风速东向量指示了近岸区域的离岸流情况，且该动力因子与海滩前滨剖面变动最强烈的b1、b8桩点呈正相关关系。结合图5，在台风影响本海区期间(即开始观测后约40～120 h)，风速东分量Wu为负值，因此实际上在台风影响期间风速东向量指示了向岸流，且为表面向岸流，底部则为离岸流[24]，而导致前滨剖面桩点b1、b8处的泥沙向海搬运。第1典型变量与入射波最大波高的相关系数为0.827 2，但这一动力因子与海滩前滨剖面变动最强烈的b1、b8桩点呈负相关关系，指示了随着台风大浪所致的波浪增水，波能的增加(如图4最大波高H的变化情况)，波浪越顶而导致桩点b1较大的侵蚀；波高增高，破波点更加向海侧，崩破波扰动桩点b8地带的泥沙，在底部离岸流作用下向海搬运。由图4、图5，向岸流与最大波高之间相关性显著，反映了台风致风浪环境下，波高增高，波能增加，而致沿岸流的增强。第1典型变量与海滩碎波尺度参数y6的相关关系较显著，相关系数为0.605 99，这一因子与海滩前滨剖面变动最强烈的b1、b8桩点呈负相关关系，反映了随海滩碎波尺度参数的增加(如图4碎波尺度参数εs的变化情况)，同样反映了海滩前滨水上和水下发生泥沙离岸搬运的事实。实际上，正是由于台风作用期间海滩泥沙向海搬运才导致海滩碎波尺度参数的增加，海滩更加消散。这一现象已被Wright和Short[25]、Short[1]所证实。

(2)由表1可得出第2典型变量占总方差的37.02%，U2与V2的典型相关系数r2为0.824 4，同样说明了海滩前滨剖面地形变化与近岸动力因子之间具有高度的相关关系。由表2、表3可知所对应的第2对标准化的典型变量的线性组合为：

U2=-0.325 6x1-0.166 4x2-0.481 3x3-

0.670 2x4-0.960 5x5-0.884 5x6-

0.158 4x7+0.493 6x8，

(6)

V2=0.175 5y1+0.743 1y2+0.319 1y3-

0.368 0y4+0.565 0y5-0.421 0y6，

(7)

由式(6)、(7)可知，第2典型变量与桩点b1～b7都呈负相关，与桩点b8呈正相关，指示了在近岸动力因子作用下海滩前滨泥沙向海搬运而形成水下沙坝的过程，这是海滩前滨剖面地形变化的次要模式。其中，第2典型变量与桩点b4、b5、b6关系密切(相关系数分别为-0.670 2、-0.960 5和-0.884 5)，尤其与桩点b5的相关系数高达-0.960 5，反映了近岸动力因子对海滩岸坡底部的强烈冲刷(冲刷成凹槽)。

第2典型变量与近岸动力因子最大波高y1、最大波周期y2、风速东分量y3、海滩地下水位y5呈正相关关系，与风速北分量y4和碎波尺度参数y6呈负相关关系。其中，第2典型变量与海岸动力因子组中的最大波周期(相关系数为0.743 1)和海滩地下水位(相关系数为0.565 0)这两个因子关系密切。最大波周期与桩点b1～b7都呈负相关关系，指示了随着波浪周期的增加，海滩前滨遭受更大的侵蚀。但实际情况是，在风暴致风浪环境中，波高大、周期短(如图4最大波周期T的变化情况)的风暴浪作用于消散型海滩，但为何发生了海滩前滨的强烈侵蚀？这一“矛盾”的自然现象早已引起研究人员的关注，并促进了近岸长重力波(波浪周期界于20～200 s)变化的研究。相关研究指出，入射波能在暴风浪时，内碎波带内的波能变化与正常海况相同，暴风浪只是使入射波浪(周期小于20 s)的破波波高增大，破波点向海侧转移，破波带范围加大[26—29]。在消散型海滩上，长重力波频段的波能在总波能中占据主导地位[27]。Short指出，在风暴作用下，波能增加，并向长重力波频转移，表现为岸线处的波浪增水与减水[1]。其中桩点b5变动最为强烈的原因，正是在这种长重力频带周期波浪作用下，海滩底部才造成更大的侵蚀[14]。海滩地下水位对海滩前滨剖面地形变化的次要模式的影响与最大波周期比较相似，同样桩点b1～b7呈负相关关系，海滩地下水位的变动指示了潮汐对海滩前滨剖面地形的影响。潮汐水位波动可拓展入射波对海滩前滨地形(b1～b7)的影响，尤其是台风作用下会导致海岸发生更大的波浪增水，抬升海滩地下水位。落潮阶段海滩地下水面向海倾斜，从海滩内抬升的地下水位中渗出的水量将加强后退流对前滨地形的冲刷强度，尤其在桩点b5处，使泥沙向海搬运。

(3)第3典型变量占总方差的12.27%，U3与V3的典型相关系数r3为0.474 7，相关关系较显著。由表2、表3可知所对应的第3对标准化的典型变量的线性组合为：

U3=0.186 1x1+0.652 3x2+0.352 0x3-

0.326 4x4-0.036 8x5-0.129 0x6-

0.610 6x7-0.492 7x8，

(8)

V3=-0.500 6y1-0.333 8y2+0.061 1y3-

0.691 2y4+0.523 3y5+0.292 5y6，

(9)

由式(8)、(9)可知，第3典型变量与桩点b1、b2、b3呈正相关，与桩点b4～b8呈负相关，指示了在近岸动力因子作用下，海滩前滨上部堆积、下部侵蚀的过程。其中第3典型变量与桩点b2、b7关系密切，但与桩点b2呈正相关关系，相关系数为0.652 3；而与桩点b7呈负相关关系，相关系数为-0.612 6。

第3典型变量与近岸动力因子最大波高y1、最大波周期y2、风速北分量y4呈负相关关系，与风速东分量y3、海滩地下水位y5、碎波尺度参数y6呈正相关关系。其中，第3典型变量与风速北向量、海滩地下水位和最大波高关系等动力因子关系密切。第3典型变量与风速北向量呈负相关关系，相关系数为-0.691 2。风速北向量指示了近岸泥沙的沿岸流搬运，这一动力因子与海滩前滨上部区域(b1～b3)呈负相关关系，与海滩前滨下部区域(b4～b8)呈正相关关系，反映了在沿岸流加强情况下(如图5风速北分量Wv的变化情况)海滩前滨上部将发生侵蚀，下部淤积。沿岸流作为碎波带内与岸线平行的水体流动，流速可达到1.5 m/s而使泥沙输运，它们与海滩长期侵蚀和海港、潮汐通道变浅有关[30]。沿岸流不仅取决于入射波，也取决于风和潮汐。有关研究指出，在强风沿岸吹刮的情况下，风对沿岸流的作用力的确很显著，尤其是坡度较缓的海滩上[31-32]。第3典型变量与海滩地下水位呈正相关关系，相关系数为0.523 3，这一动力因子与海滩前滨上部区域(b1～b3)呈正相关关系，与海滩前滨下部区域(b4～b8)呈负相关关系，体现了涨潮过程对海滩前滨地形的影响。涨潮时，海滩地下水位向岸倾斜，上冲流携带的部分流量渗入海滩内部使得上冲流作用强度减弱，海滩前滨上部地形趋于加积。第3典型变量与最大波高的关系较紧密，相关系数为-0.500 6，这一动力因子与海滩前滨上部区域(b1～b3)呈负相关关系，与海滩前滨下部区域(b4～b8)呈正相关关系，反映了台风作用下海滩前滨上部侵蚀而下部淤积的情况，与第1典型变量中最大波高所控制的前滨地形变化过程明显不同，进一步佐证了海滩地形动力过程是一个复杂的非线性耦合机制。

(4)第4典型变量占总方差的9.00%，U4与V4的典型相关系数r4为0.406 5，相关关系较显著。由表2、表3可知所对应的第4对标准化的典型变量的线性组合为：

U4=-0.151 1x1+0.225 0x2+0.225 7x3-

0.198 1x4+0.183 9x5+0.071 0x6-

0.183 4x7+0.317 9x8，

(10)

V4=-0.075 6y1-0.168 0y2-0.020 2y3+

0.606 6y4+0.362 0y5+0.171 0y6，

(11)

由式(10)、(11)可知，第4典型变量与剖面各高程点的相关系数都不大，最大相关系数的绝对值仅为0.32，与桩点b1、b4、b7呈负相关关系，与桩点b2、b3、b5、b6、b8呈正相关关系。而第4典型变量与风速北分量呈正相关关系，相关系数的绝对值大于0.6，尽管统计检验结果表明第4典型变量属于高置信水平的显著典型变量，但沿岸流增强如何导致海滩前滨剖面地形发生侵蚀—淤积—侵蚀—淤积—侵蚀—淤积这样的过程，从海岸地形动力过程的角度难以给出较明确的解释。

5 结论

本文基于0709号台风“圣帕”影响下粤东后江湾的现场实测海滩前滨地形资料和水动力、风等因子资料，采用典型相关分析海滩前滨剖面不同部位与近岸动力因子之间的关系，识别出台风影响下海滩前滨地形不同的变化过程，揭示了这些变化过程不同的控制因子，并给出了物理解释，得到如下的结论：

(1)台风影响下后江湾海滩前滨地形的主要变化过程是水上滩肩被破坏—水下岸坡略有堆积—水下沙坝泥沙向海搬运；控制这一地形变化过程的主要动力因子是风速东向量、最大波高和碎波尺度参数。实测台风影响下风速东向量方向为向岸，实为表面向岸流，底部为离岸流。台风影响下近岸增水，波高增高，波能增加，加强了向岸流，波浪越顶作用于海滩前滨水上地带，破波点向海移动，崩破波扰动水下岸坡海侧地带泥沙，在底部离岸流的作用下，使这两个地带发生侵蚀。海滩碎波尺度参数则是上述两个动力因子作用的结果，而导致台风影响下海滩更加消散。

(2)台风影响下后江湾海滩前滨地形的次要变化过程是海滩前滨泥沙向海搬运而形成水下沙坝。控制这一地形变化过程的主要动力因子是最大波周期和海滩地下水位，增加的波浪周期实际上是长重力波对这一过程的直接控制；台风影响下，岸线波浪增水抬升地下水位，落潮阶段加强的后退流也加强了这一过程。

(3)台风影响下后江湾海滩前滨地形的变化过程也表现出前滨上部地带堆积、下部侵蚀的变化过程。控制这一地形变化过程的主要动力因子是沿岸流、海滩地下水位和最大波高。沿岸流对这一过程主要是通过沿岸流所致泥沙的沿岸输运；海滩地下水位主要是通过涨潮时的上冲流对这一过程进行控制。最大波高又一次对这一过程进行作用，佐证了海滩地形动力过程是一个复杂的非线性耦合机制。

(4)上述3条结论进一步揭示了台风影响下海滩前滨地形动力过程是由多个不同的地形—动力过程耦合作用而组成。同时，也表明CCA法是理解海岸地形动力过程较好的研究方法。

[1] Short A D. The role of wave height，period，slope，tide range and embaymentisation in beach classification: a review[J]. Revista Chilena de Historia Natural，1996，69: 589-604．

[2] Birkemeier W A. The effects of the coastal storm on beaches in North Carolina and New Jersey[J]. Shore and Beach，1979，47: 7-15．

[3] Dolan R，Davis R E. Coastal storm hazards[J]. Journal of Coastal Research，1994，SI(12): 103-114．

[4] Lee G H，Nicholls R J，Birkemeier W A. Storm-driven variability of the beach-nearshore profile at Duck，North Carolina，USA，1981-1991[J]. Marine Geology，1998，148(3/4): 163-177．

[5] Forbes D L，Parks G S，Manson G K，et al. Storms and shoreline retreat in the southern Gulf of St. Lawrence[J]. Marine Geology，2004，210: 169-204．

[6] Karunarathna H，Pender D，Ranasinghe R，et al. The effects of storm clustering on beach profile variability[J]. Marine Geology，2014，348：103-112．

[7] Qi H S，Cai F，Lei G，et al. The response of three main beach types to tropical storms in South China[J]. Marine Geology，2010，275: 244-254．

[8] De Vriend H J. Mathematical modelling and large-scale coastal behavior: Part 1. Physical processes[J]. Journal of Hydraulics Research，1991，29(6): 727-740．

[9] Larson M，Kraus N C. Prediction of cross-shore sediment transport at different spatial and temporal scales[J]. Marine Geology，1995，126(1/4): 111-127．

[10] Larson M，Capobianco M，Hanson H. Relationship between beach profiles and waves at Duck，North Carolina，determined by canonical correlation analysis[J]. Marine Geology，2000，163(1/4): 275-288．

[11] Horrillo-Caraballo J M，Reeve D E. An investigation of the link between beach morphology and wave climate at Duck，North Carolina，USA[J]. Journal of Flood Risk Management，2008，1(2): 110-122．

[12] Horrillo-Caraballo J M，Reeve D E. An investigation of the performance of a data-driven model on sand and shingle beaches[J]. Marine Geology，2010，274(1/4): 120-135．

[13] Hansen J E，Barnard P L. The observed relationship between wave conditions and beach response，Ocean Beach，San Francisco，CA[J]. Journal of Coastal Research，2009，SI(56): 1771-1775．

[14] 陈子燊，李志龙，陈建耀，等. 常波况下前滨剖面地形动力过程分析[J]. 海洋通报，2007，26(3): 12-18.

Chen Zishen，Li Zhilong，Chen Jianyao，et al. Analysis on Morphodynamic processes of foreshore profile under normal wave conditions[J]. Marine Science Bulletin，2007，26(3): 12-18．

[15] Guza R T，Inman D L. Edge waves and beach cusps[J]. Journal of Geophysical Research，1975，80(21): 2997-3012．

[16] Wright L D，Short A D. Morphodynamic of beaches and surf zones in Australia[M]// Komar P D. Handbook of Coastal Processes and Erosion. Florida: CRC Press，1983: 35-64．

[17] Short A D. Beach systems of the central Netherlands coast: Processes，morphology and structural impacts in a storm diven multi-bar system[J]. Marine Geology，1992，107(1/4): 103-137．

[18] Short A D. Multiple offshore bars and standing waves[J]. Journal of Geophysical Research，1975，80: 3838-3840．

[19] Aagaard T. Infragravity waves and nearshore bars in protected，strom-dominated coastal environments[J]. Marine Geology，1990，194(1/4): 181-203．

[20] Bowman D，Goldsmith V. Bar morphology of dissipative beaches: an empirical model[J]. Marine Geology，1983，51(1/4): 15-33．

[21] Hotelling H. Relations between two sets of variants[J]. Biometrika，1936，28(3/4): 321-377．

[22] Rózyński G. Data-driven modelling of multiple longshore bar evolution and interactions[J]. Coastal Engineering，2003，48 (3): 151-170．

[23] 魏凤英. 现代气候统计诊断预测技术[M]. 北京: 气象出版社，1999．

Wei Fengying. Modern Climatic Statistical Diagnosis and Prediction Technology[M]. Beijing: China Meteorological Press，1999．

[24] Dean R G. Heuristic models of sand transport in the surf zone[C]//Proceeding of Conference on Engineering Dynamics in the Surfzone. New York,Soc of Civ Eng，1973: 208-214．

[25] Wright L D，Short A D. Morphodynamic variability of surf zones and beaches: A synthesis[J]. Marine Geology，1984，56(1/4): 93-118．

[26] Homan R A. Infragravity Energy in the Surf Zone[J]. Journal of Geophysical Research，1981，86(C7): 6442-6450．

[27] Gaza R T，Thornton E B. Swash Oscillations on a Natural Beach[J]. Journal of Geophysical Research，1982，87(C1): 483-491．

[28] Holman R A，Sallenger A H. Setup and Swash on a Natural Beach[J]. Journal of Geophysical Research，1985，90(C1): 945-953．

[29] Holman R A. Extreme value statistics for wave run-up on a natural beach[J]. Coastal Engineering，1986(9): 527-544．

[30] Short A D. Handbook of Beach and Shoreface Morphodynamics[M]. John Wiley & Sons，LTD，1999: 94-96．

[31] Nummedal D，Finley R J. Wind-generated longshore currents[C]//Proceedings 16th International Conference on Coastal Engineering. ASCE，1978: 1428-1438．

[32] Whitford D J，Thornton E B. Comparison of wind and wave forcing of longshore currents[J]. Continental Shelf Research，1993，13(3):1205-1218．

Study on beach morphodynamic processes of Houjiang Wan in East Guangdong under the influence of the typhoon (No. 0709)

Yu Jitao1，2，Ding Yuanting1，Cheng Huangxin3，Chen Zishen4

(1.SchoolofSurveyingandLandInformationEngineering，HenanPolytechnicUniversity，Jiaozuo454000，China; 2.SchoolofEnvironmentalStudies，ChinaUniversityofGeoscience(Wuhan)，Wuhan430074，China; 3.ArtsandMediaSchool,ChinaUniversityofGeosciences(Wuhan),Wuhan430074,China;4.GeographyandPlanningSchool，SunYat-senUniversity，Guangzhou510275，China)

Based on the foreshore topography，water dynamics and wind data on Houjiangwan beach in East Guangdong，this paper used the method of canonical correlation analysis to identify different morphodynamic foreshore processes under the influence of the typhoon “Sepat” (No. 0709)，and revealed some primary dynamic factors controlling these foreshore processes and attempted to present the physical interpretations. The analytical results included that (1) the primary foreshore process consisted of the eroded subaerial zone with the destroyed berm，the slightly depositional submarine slope zone and the bar zone with sediment movement offshore，and the process was controlled by several factors such as the eastern component of the wind speed，the maximum wave heights and the surf scaling parameter; (2) the secondary terrain process was the formation of submarine bar due to the sediment being transported from the foreshore to offshore，and the process was dominated by two dynamic factors such as the maximum wave periods and the beach underground water levels; and (3) the foreshore morphology was also characterized by the accumulation of the upper zone and the erosion of the lower zone of the foreshore，and the process was controlled by the following factors，i.e.，the longshore currents，the beach underground water levels and the maximum wave heights. Finally，this study proposed that the morphodynamic processes of the foreshore are coupled by many different morphological and dynamic processes．

morphodynamic processes; foreshore; typhoon; canonical correlation analysis

10.3969/j.issn.0253-4193.2015.05.008

2014-03-19；

2014-09-05。

国家自然科学基金资助项目(41301005)；中国博士后科学基金资助项目(2014M552118)。

于吉涛(1981—)，男，山东省威海市人，博士，讲师，研究方向为自然地理学。E-mail：ddyjt@163.com

*通信作者：陈子燊，教授，从事海岸环境演变与工程应用研究。E-mail：eesczs@mail.sysu.edu.cn

P737.1

A

0253-4193(2015)05-0076-11

于吉涛，丁圆婷，程璜鑫，等. 0709号台风影响下粤东后江湾海滩地形动力过程研究[J]. 海洋学报，2015，37(5)：76-86，

Yu Jitao，Ding Yuanting，Cheng Huangxin，et al. Study on beach morphodynamic processes of Houjiang Wan in east Guangdong under the influence of the typhoon (No. 0709)[J]. Haiyang Xuebao，2015，37(5)：76-86，doi：10.3969/j.issn.0253-4193.2015.05.008