矩形巷道围岩散热规律数值模拟研究

刘彦青，宇 星

(中国矿业大学(北京) 资源与安全工程学院， 北京 100083)

矩形巷道围岩散热规律数值模拟研究

刘彦青1，宇 星1

(中国矿业大学(北京) 资源与安全工程学院， 北京 100083)

针对矩形巷道围岩散热规律，建立二维巷道围岩散热模型，采用有限体积法对巷道围岩温度场进行解算，计算模型中考虑了构成巷道围岩的不同岩层的物性差异。利用计算数据拟合曲线方程方法得到巷道围岩散热速率公式，该式可适用于煤巷与岩巷，最后推导得出整段巷道围岩散热速率公式,包括掘进巷道与使用中巷道，对制定井下热害防治措施具有一定的指导意义。

数值模拟；围岩温度场；物性差异；围岩散热速率

0 引 言

前人在围岩温度场数值模拟研究过程中将围岩视为具有各向同性单一的均质介质[1-6]，数学模型比较理想化，没有考虑到地层中不同岩层之间的物理性质差别，致使围岩温度场解算结果偏离实际围岩温度场。其中煤体与岩体的物理性质差别较大，包括密度、比热、导热系数等，煤巷围岩散热与岩巷围岩散热存在一定差别。本文考虑了岩体与煤体的物理性质差异，以及沿层面方向与垂直于层面方向的导热系数差别，深入分析研究了煤巷与岩巷的围岩散热规律。

1 巷道围岩散热模型的建立

1.1 物理模型的建立

模型一为岩巷，作为参照模型，模型中煤层的顶底板岩层性质相同，重点分析煤层对于煤巷围岩散热的影响，针对3种煤巷形式分别建立了3个物理模型，模型二为半岩巷煤巷，煤层为薄煤层，模型三为全煤厚掘进煤巷，煤层为中厚煤层，模型四为沿煤层底板巷道，煤层为厚煤层。

模型中煤巷形状为矩形，实际情况中煤巷形状大多为梯形，前人研究[7,8]表明围岩温度场受巷道形状的影响范围仅限于靠近巷壁的很小一段距离，相对于整体围岩温度场而言，巷道形状的影响可忽略。

1.2 数学模型的建立

1.2.1 假设条件

(1) 煤层为单一均质的介质，沿层面方向导热系数大于垂直于层面方向导热系数，忽略煤层瓦斯运移的影响，不考虑煤层氧化放热影响；

(2) 顶底板为单一均质的介质，沿层面导热系数大于垂直于层面的导热系数；

(3) 未考虑巷道壁面水分蒸发影响。

1.2.2 控制方程及解算条件

围岩散热问题是二维导热问题，考虑了煤层与顶底板岩层为层状介质，其沿层面方向导热系数与垂直于层面方向导热系数差别较大，式(1)为二维的导热微分方程。

(1)

边界条件：计算区域边界处热流密度为0，即第二类边界条件(绝热边界条件)，见式(2)，巷壁处为第三类边界条件，见式(3)。

(2)

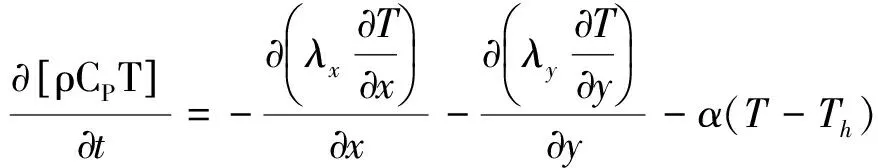
(3)

初始条件：巷道刚掘开时围岩各处温度均为原始岩温。

式中,T为温度，k;t为时间，s;λ为导热系数，W/(m·k)，ρ为围岩密度，kg/m3;Cp为围岩的比热容，J/(kg·k);α为对流换热系数，W/(m2·k);Th为巷道风流温度，k;

2 数值解算及结果分析

2.1 网格划分

巷道围岩散热物理模型具有对称型，计算区域采用结构式网格划分方式，易于实现非均质巷道围岩参数赋值,见图1。

图1 网格划分示意图

2.2 控制方程离散

根据计算区域网格划分形式，对导热方程采用基于有限体积法的C-N格式进行离散，每个节点离散方程中均包含10个温度值，即当前时刻与该节点相邻的四个温度值、前一时刻该节点温度值、前一时刻与该节点相邻的四个节点的温度值，其中当前时刻温度值为未知量，上一时刻温度值为已知量。通过求解方程组计算得到当前时刻计算区域内温度场。

该算法可以保证在计算过程中时刻满足质量守恒定律，解算结果具有物理真实性。

2.3 解算程序编制

利用vb语言编制了解算程序，程序结构流程见图2。

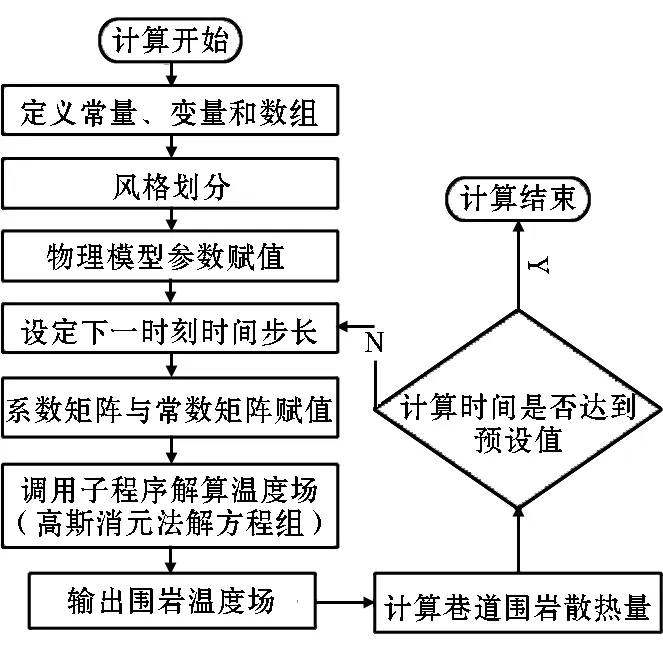
图2 程序流程图

2.4 解算结果

2.4.1 计算参数选取

数值模拟计算中基本参数设置见表1。

2.4.2 巷道围岩温度场分布

图3、图4为巷道围岩温度场解算结果图，模型一中围岩温度降低区域明显大于后三种模型，且模型四中围岩温度降低区域最小，说明煤层存在影响了巷道围岩温度场分布。

表1 数值模拟基本参数

图3 巷道暴露28 d后四种模型围岩温度场

图4 巷道暴露169 d后四种模型围岩温度场

2.4.3 掘进巷道围岩散热速率

图5为巷道巷壁散热速率-时间的对数图，从图中可看出厚煤层煤巷与岩巷的巷壁散热速率差别最大，即煤层愈厚，巷壁围岩散热愈小。

采用解算数据拟合方法可得到巷道围岩散热速率公式，拟合公式见式(4)，拟合系数见表2，式中a值、b值与巷道围岩条件(岩层导热系数、岩层厚度、岩层密度等)、巷道条件(巷道的形状、尺寸、风流大小等)密切相关：

由表中R2可知该式对各种条件下巷壁围岩散热速率曲线的拟合程度高，该式可用于描述巷道围岩散热速率。

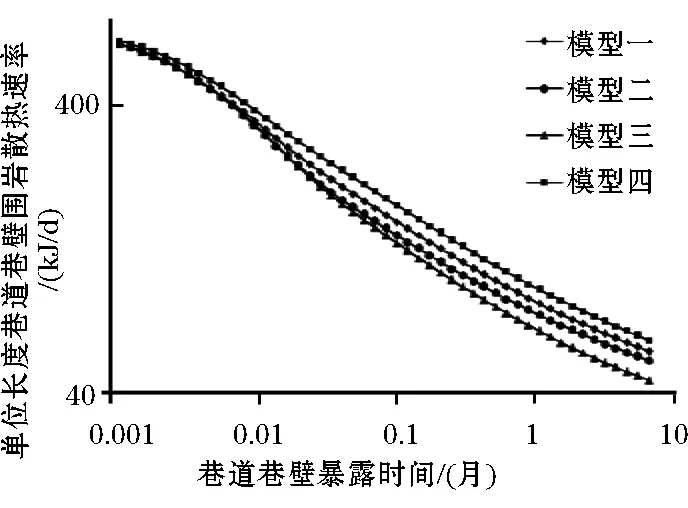
图5 巷道巷壁围岩散热速率(对数图)

(4)

表2 拟合式系数表

2.5 整段巷道围岩散热速率

2.5.1 掘进中巷道围岩散热速率

掘进巷道的已掘巷道巷壁围岩散热速率随着暴露时间增大而衰减。掘进巷道巷壁围岩散热速率可通过对各段巷道巷壁围岩散热速率进行积分求得，见式(5)。

(5)

式中，l为已掘巷道长度，m；v为巷道掘进速度,m/d。

2.5.2 使用中巷道围岩散热速率

已使用巷道的暴露时间为巷道掘进时间和巷道使用时间之和，其巷壁围岩散热速率较掘进巷道小，式(6)为t时刻整段巷道围岩散热速率。

(6)

式中，t为该巷道掘进时间与使用时间之和，单位为月；

2.5.3 整段巷道围岩散热速率公式参数求解

整段巷道围岩散热速率公式确定的关健之处在于如何得到a值、b值，而其他参数如掘进速度、巷道长度等为已知量。

上文已验证了不同条件下巷道围岩散热速率公式均可由式(4)表示，因此可根据式(4)，将数值模拟解算结果中任意两个不同时刻下的巷道围岩散热速率分别代入式(4)中联立可求解得一组a值与b值。

为了得到比较精确的a值与b值，可以选取多组巷道围岩散热速率结果求解得到多组a值与b值，然后分别对a值与b值求平均值。

在上述研究基础上，编制了巷道围岩散热速率解算软件，该软件主要包括围岩温度场求解模块与整段巷道围岩散热速率公式参数求解模块。

3 结 论

(1) 建立了非均质的、各向异性的、非稳态的二维巷道围岩散热模型，利用VB程序语言编制了计算软件，进行了数值解算，解算结果显示了煤巷与岩巷围岩散热具有明显差异性，说明将巷道围岩视为单一的均质的介质会造成一定程度偏差，研究巷道围岩散热必须考虑围岩的物性差异。

(2) 采用数据拟合曲线方式得到了巷道围岩散热速率公式，该公式对煤巷与岩巷围岩散热计算结果拟合程度极高，具有普遍适用性。

(3) 根据巷道围岩散热速率公式推导出整段巷道围岩散热速率公式、已使用巷道巷壁围岩散热速率公式，并给出如何确定公式参数的方法，编制了巷道围岩散热速率解算软件，具有现场实用性。

[1]樊小利，张学博.围岩温度场及调热圈半径的半显式差分法解算[J].煤炭工程,2011(7):82-84.

[2]秦跃平，王 健，郝永江等.基于有限体积法的巷道围岩散热无因次分析[J].矿冶工程，2013,33(3)：5-7.

[3]胡增辉,李晓昭,赵晓豹，等.隧道围岩温度场分布的数值分析及预测[J].地下空间与工程学报,2009,5(5):867-872.

[4]秦跃平，秦凤华，于明学．用有限单元法研究回采工作面围岩散热[J].辽宁工程技术大学学报(自然科学版)，1999,18(4):342-346．

[5]周西华，单亚飞，王继仁.井巷围岩与风流的不稳定换热[J].辽宁工程技术大学学报(自然科学版),2002,21(3):264-266.

[6]牛平安.利用 Fluent软件模拟跃进煤矿巷道风温变化规律[J].煤炭与化工，2013，36(4)：10-12.

[7]张习军, 姬建虎, 陆 伟.深热矿井巷道围岩的热分析[J].煤矿开采,2009,14(2):5-7.

[8]侯棋棕,沈伯雄.调热圈半径及其温度场的数值解算模型[J].湘潭矿业学院学报,1997,12(1):9-16.

2014-07-23)

刘彦青 (1989-)，男，山西忻州人，硕士研究生，Email：lyqing0906@163.com。