液晶动态响应实验研究

刘晓梦，布秀敏，秦 禹，孙艳梅，叶文江

（1．河北工业大学理学院，天津 300401；2．河北交通职业技术学院，河北石家庄 050091；3．河北工业大学信息工程学院，天津 300401；4．正定县第八中学，河北石家庄 050800）

液晶动态响应实验研究

刘晓梦1，布秀敏2，秦 禹3，孙艳梅4，叶文江1

（1．河北工业大学理学院，天津 300401；2．河北交通职业技术学院，河北石家庄 050091；3．河北工业大学信息工程学院，天津 300401；4．正定县第八中学，河北石家庄 050800）

为了分析液晶的响应时间并判断其响应速度，开发了液晶动态响应测试装置，并对强锚泊扭曲排列向列液晶的动态响应过程进行了测量。当脉冲信号施加于液晶盒上时，液晶的响应时间，即上升时间随电压的增大而减小；当脉冲信号撤消时，液晶的响应时间，即下降时间基本保持不变。与液晶动力学理论数值计算结果进行比较表明，实验结果和理论结果基本吻合。

液晶；动态响应；响应时间；扭曲向列相；动力学理论

液晶器件的动态响应时间是指在施加输入信号后，液晶显示由亮变暗再到亮，或者由暗变亮再到暗所用的时间［1］。响应时间分为上升时间和下降时间，一般情况下所说的响应时间为两者的总和。人在观测高速运动的画面时，大脑中会产生短暂的印象。动态显示的原理就是利用了人眼的这种视觉残留，使渐变的的图像连续显示，从而形成动态的影像。人的视觉能接受的画面播放速度为25个／s，即每个画面约40 ms。当液晶的响应时间过长时，显示画面就会出现残影和拖曳现象，观看者会明显感到画面停顿。因此，动态响应的快慢是衡量液晶显示质量的一个重要指标。对于液晶动态响应的研究，有利于降低液晶器件响应时间，提高响应速度［2］，减少显示动态画面时的迟滞，提高显示性能使画面更加完美。

液晶动态响应实验，主要研究在电压施加和撤去过程中，液晶分子位形变化的过程。分子位形变化导致液晶盒的透射光强发生变化，液晶的动态响应过程最终反映为液晶盒的光学透过率在电压变化过程中随时间的变化关系。本文开发了液晶动态响应实验装置，并利用该装置对强锚泊边界条件下的扭曲排列向列液晶的动态响应过程进行测量，得到了与理论上数值计算结果相吻合的液晶盒的光学透过率随时间的变化关系。

1 液晶动态响应实验装置

液晶动态响应实验装置如图1所示，由He－Ne激光器（632．8nm）、起偏器、液晶盒（TN）、检偏器、信号采集装置（硅光探测器、信号采集卡和单脉冲信号源等）构成。起偏器和检偏器正交放置，TN盒水平摩擦基板与起偏器对应，垂直摩擦基板与检偏器对应，且水平摩擦方向与起偏器的透光轴成45°角。

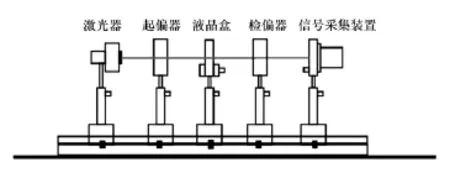
图1 液晶动态响应实验装置图

He－Ne激光器发出的激光经起偏器后变成沿其透振方向振动的线偏振光。对TN盒施加单脉冲信号，液晶分子由于本身具有电学性质，会在电场作用下定向排列。定向排列后的液晶具有和晶体一样的双折射效应，会使光的偏振状态发生变化。偏振光透过液晶盒再穿过检偏器，其光强也会发生变化。使用信号采集卡可以记录电场变化过程中透射光强随时间变化关系，由Origin绘图软件［3－4］可以得到TN盒动态响应实验曲线［5－6］。改变单脉冲信号源的幅度，可以测得不同电压下的动态响应实验曲线。

脉冲信号的产生主要由单片机最小系统［7］和模拟电压输出模块［8］两部分组成，其中模拟电压输出模块主要由LCD驱动电压幅值控制器、A路DA转换和B路DA转换3部分构成。电压脉冲信号产生原理：单片机最小系统经管脚传输一列数字信号给数模转换芯片DAC0832，数模转换芯片内部会依据此数字信号输出一电流量，再经由运算放大器和减法器电路，最终输出一个与数字信号相关连的模拟电压量，即是给液晶盒提供脉冲信号的电压参量。此电路可输出0～10．0 V的电压脉冲，最小步进值为0．04V，可精确输出任意幅值电压脉冲信号。本实验中脉冲信号的宽度为200ms，数据采集的时间为300ms。脉冲信号产生系统实物见图2。

2 液晶动态响应理论分析

2．1 扭曲向列相动力学方程

扭曲向列相（TN）液晶盒中液晶指向矢动力学响应由Erickson－Leslie方程描述［9］：

图2 脉冲信号产生系统实物图

其中：γ为液晶的转动黏滞系数；K11、K22和K33分别为液晶的展曲、扭曲和弯曲弹性常数；q＝2π／P，P为液晶的螺距；ε0为真空中的介电常数；Δε为平行与垂直于液晶分子长轴的介电常数之差，Δε＝ε／／－ε⊥；E为液晶层中的电场强度，E＝U／d，U为施加在液晶层上的电压，d为液晶层厚度；θ和分别为指向矢的倾角和方位角，都是盒厚位置（z）的函数。

对于上下基板均为强锚泊情形的扭曲向列相液晶盒，上下基本的扭曲角度固定，总扭曲角度为Φ。采用文献［10］中的处理方法，撤掉电压和施加电压时液晶指向矢的响应时间记为τoff和τon，有：

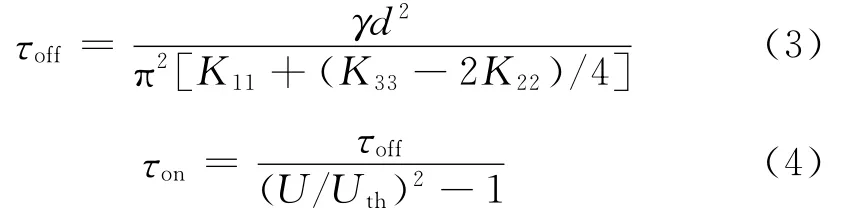
其中Uth为液晶盒的阈值电压，相应的阈值电场为［11－12］

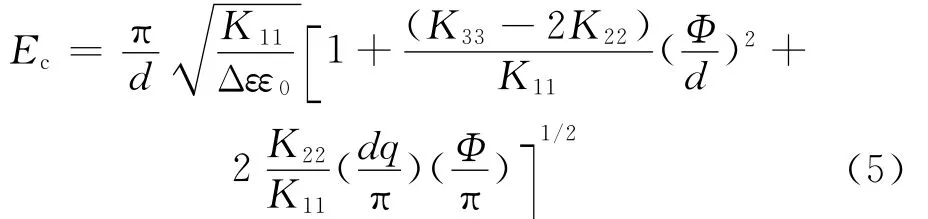
2．2 液晶指向矢的模拟

液晶指向矢的模拟见文献［13］。在很多液晶器件中，液晶指向矢分布只能得到数值解［14］，指向矢变化的动力学方程可以用来计算指向矢结构的数值解［15］。在平衡态下［16］，液晶盒系统总的自由能最小，指向矢倾角θ和方位角满足Euler－Lagrange方程［17］：

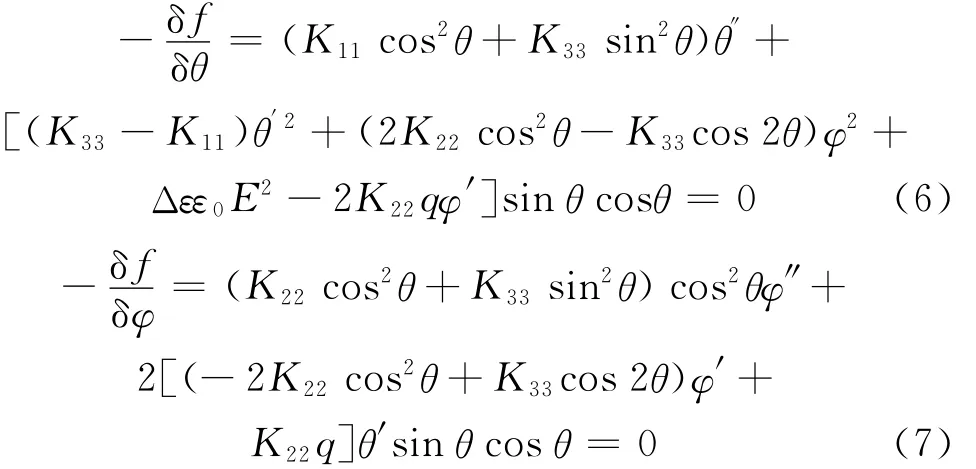
若起初系统不处于平衡态，其将向平衡态变化，动力学方程为：

式中f为自由能，u、w为变量。

利用上述方程，可以由t时刻液晶指向矢的角度计算出t＋Δt时刻液晶指向矢的角度：

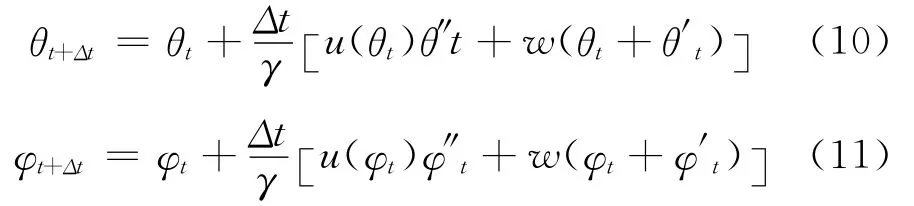
模拟过程中，将整个液晶层分为N个厚度非常薄的子层，每一子层对应的位置可以看作是节点，采用弛豫法［18］，第i个节点处液晶指向矢的角度可以通过下式计算［19］：

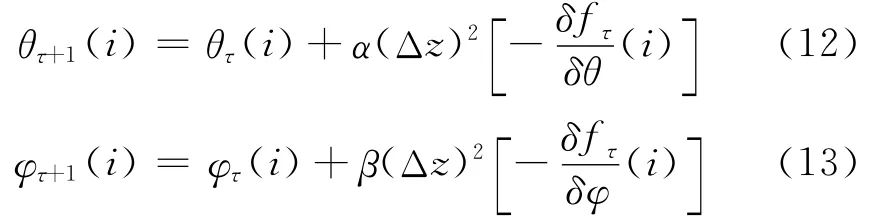
其中α和β是弛豫常数。

2．3 光学透过率的模拟

光学透过率的模拟见文献［20－21］。在模拟计算光学透过率时，与液晶指向矢计算相对应，同样将液晶层分为N个厚度非常薄的子层。第i个子层的琼斯矩阵为

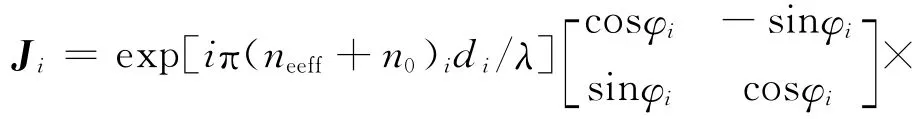
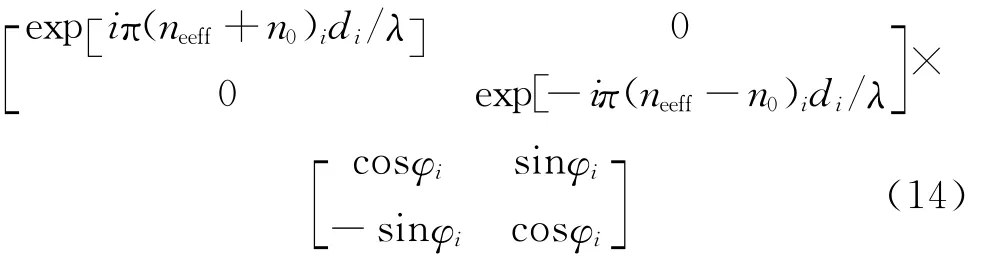
式中di为第i个小薄层的厚度，λ为入射偏振光的波长，neeff为非常光的折射率：

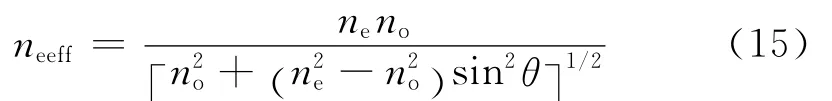
式中，no为o光折射率，ne为e光折射率。通过将各个光学元件的矩阵依次相乘，可以得到光线的出射偏振态

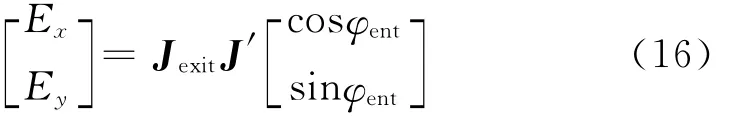
其中ent为起偏片的方位角。液晶盒的光学透射率表达式为

结合式（17）和上述指向矢分布，分层使用琼斯矩阵重复计算，即可模拟得到穿过液晶盒的光透过率与时间的变化曲线，即液晶动态响应的理论曲线。

3 理论与实验结果比较

通过图1所示的实验装置，对常白模式的TN盒的动态响应进行测定，并对采集到的实验数据进行归一化处理，得到了对应3、4、5、6V脉冲时液晶的动态响应实验曲线。理论计算时，液晶材料的参数：K11＝9．0pN、K22＝6．0pN、K33＝12．1pN、!"＝4．9、#!＝11．59、$＝0．08N·s／m2、ne＝1．616、no＝1．521、P＝2mm，液晶盒厚度为d＝5%m，起偏片的方位角ent＝45°，检偏片的方位角与起偏片方位角相互垂直，入射光的波长为&＝632．8nm。实验曲线和模拟得到的结果见图3。

通过分析在不同电压下的TN盒动态响应曲线，可以发现：随施加电压的增加，施加脉冲信号所对应的上升时间逐渐减小，而撤去脉冲信号所对应的下降时间基本保持不变，与动力学理论给出的结果保持一致。

4 结论

通过研究施加和撤去电压瞬间液晶的动力学响应，得出液晶形变随时间的变化关系，进而得到液晶盒的光学响应（透过率）随时间变化关系。通过实验测得的结果，可以得出强锚泊边界条件下的扭曲向列相液晶盒的响应时间随电压的增大而减少，响应速度随电压增大而加快。上述实验结果与理论计算得到的结果基本吻合。

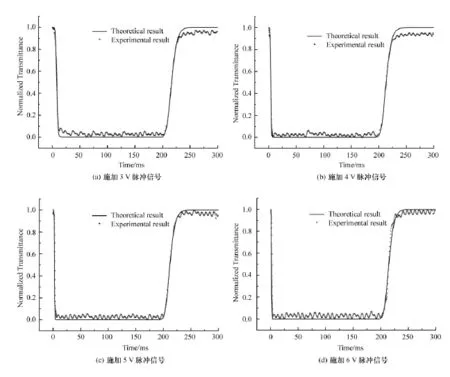
图3 施加不同电压脉冲信号时归一化透过率随时间的变化曲线

（References）

［1］范志新．液晶器件工艺基础［M］．北京：北京邮电大学出版社，2000：189－199．

［2］Bos P，袁军涛，石琳．显示器的快速响应液晶效应［J］．现代显示，2008（4）：9－14．

［3］易均辉，莫惠媚，龚福忠，等．巧用Origin软件处理物理化学实验数据［J］．实验室研究与探索，2009，28（8）：56－59．

［4］牟中飞，吴福根，胡义华，等．Origin软件在物理实验数据处理中的应用［J］．实验科学与技术，2009（4）：60－62．

［5］周璇，张志东，孙玉宝．有效粘滞系数对混合排列向列相液晶动力学的影响［J］．液晶与显示，2009，24（2）：168－173．

［6］张志东，范志新，黄锡珉．电控双折射液晶显示的动力学模拟计算［J］．液晶与显示，1998，13（1）：4－9．

［7］任晓荣．单片机系统可靠性设计［J］．计算机测量与控制，2003（8）：621－623，626．

［8］秦德明，徐启国．一种构思新颖的模拟数字转换电路［J］．计算机自动测量与控制，1995（1）：44－46．

［9］刘兰明．液晶动力学方程数学研究［D］．上海：复旦大学，2012．

［10］孙玉宝．液晶显示器动力学响应研究［D］．天津：河北工业大学，2010．

［11］Scheffer T，Nehring J．Twisted nematic and super－twisted nematic mode LCDs，in Liquid crystals applications and uses［M］．Bahadur：World Scientific，Singapore，1990．

［12］Raynes E P．The theory of super－twist transitions［J］．Mol Cryst Liq Cryst，1986（4）：1－5．

［13］王谦，何赛灵．液晶指向矢分布的模拟和比较研究［J］．物理学报，2001，50（5）：926－932．

［14］张志东，叶文江，邢红玉．液晶盒中挠曲电效应的计算［J］．计算物理，2004，31（2）：156－160．

［15］凌志华，蒋敏，黄锡珉，等．向列相液晶盒中液晶指向矢的分布及其显示特性的计算机模拟［J］．液晶通讯，1993，1（1）：17－22．

［16］关荣华．液晶平衡态方程计算方法的研究和比较［J］．华北电力大学学报，2004，31（2）：102－104．

［17］倪敏，冯承天．变分法的Euler－Lagrange方程及其应用［J］．上海师范大学学报：自然科学版，2000（2）：98－100．

［18］Zhao Chongbin，Peng Shenglin，Liu Lianging．Effective loading algorithm associated with explicit dynamic relaxation method for simulating static problems［J］．Journal of Central South University of Technology，2009（1）：125－130．

［19］Yang D K，Wu S T．Fundamentals of Liquid Crystal Devices［M］．Chichester：John Wiley ＆Sons Ltd，2006：186－190．

［20］邢红玉，叶文江，周璇，等．挠曲电效应对向列相液晶盒响应时间的影响［J］．计算物理，2013，30（5）：727－732．

［21］叶文江，邢红玉，杨国琛．向列相液晶盒中的挠曲电体积效应［J］．计算物理，2007，24（3）：337－341．

Experimental research on dynamic response of liquid crystal

Liu Xiaomeng1，Bu Xiumin2，Qin Yu3，Sun Yanmei4，Ye Wenjiang1
（1．School of Sciences，Hebei University of Technology，Tianjin 300401，China；2．Hebei Jiaotong Vocational ＆Technical College，Shijiazhuang 050091，China；3．School of Information Engineering，Hebei University of Technology，Tianjin 300401，China；4．Zhengding No．8Middle School，Shijiazhuang 050800，China）

In order to analyze the dynamic response time and then judge the problems about the response speed of liquid crystal，the experiment equipment using for testing the dynamic response of liquid crystal has been exploited．And the dynamic response process of twisted－nematic liquid crystal with strong－anchoring is also measured．When an impulse is applied on the liquid crystal cell，the response time，or the turn－on time，decreases with increasing voltage；when the applied impulse is removed，the response time，or the turn－off time，remains unchanged in general．By comparing with the numerical calculation getting from the kinetic theory of liquid crystal，it is found that the results of theoretical calculation and the ones from experiment consist with each other．

liquid crystal；dynamic response；response time；twisted nematic；kinetic theory

O753

A

1002－4956（2015）3－0077－04

2014－08－31 修改日期：2014－10－08

国家自然科学基金项目（11274088，11374087，11304074）；河北省自然科学基金项目（A2014202123）；河北省教育厅项目（QN2014130）；河北省高校重点学科资助课题

刘晓梦（1991—），女，河北衡水，学士，从事液晶器件物理方面的研究

叶文江（1976—），男，河北石家庄，博士，副教授，应用物理系副主任，从事液晶器件物理及实验室建设与管理方面的研究工作．

E－mail：wenjiang＿ye＠hebut．edu．cn