直剪试验剪切面积计算方法对抗剪强度的影响

董 云，王永存

（1．淮阴工学院建筑工程学院，江苏淮安 223001；2．重庆交通大学土木与建筑学院，重庆 400074）

直剪试验剪切面积计算方法对抗剪强度的影响

董 云1，王永存2

（1．淮阴工学院建筑工程学院，江苏淮安 223001；2．重庆交通大学土木与建筑学院，重庆 400074）

现行直剪试验抗剪强度计算中忽视了剪切过程中随剪切位移的增大、剪切面在不断减小的实际情况，没有考虑剪切面面积对抗剪强度的影响，使得试验结果偏离试样的真实强度。为了分析剪切面面积对抗剪强度的影响，该文重新建立数学模型，提出了3种剪切面面积计算方法，通过加装剪切位移量测系统对直剪仪进行改装并进行了试验验证，分析了剪切面面积对抗剪强度的影响。研究成果提高了直剪试验抗剪强度计算的精度，使得试验结果更接近试样的真实强度。

直剪试验；剪切面面积；内摩擦角；黏聚力

抗剪强度是衡量土的安全稳定性的一个重要指标，准确地确定土的抗剪强度指标关系到工程的安全性以及经济性。目前，测量土的抗剪强度指标的主要试验方法有直接剪切试验和三轴剪切试验。而直剪试验因其结构简单、易于操作，成为岩土工程领域最常使用的获得土体、节理以及特定材料强度的试验方法。因此，正确高效地进行直剪试验数据处理与分析，使得结果尽可能地接近土体真实值显得尤为重要。但是，目前直剪试验中使用的仪器和数据处理方法2个方面均存在明显缺陷。在仪器改进方面，一些学者［1－4］给出了合理的改进意见。但在计算方法中，一些学者仅对试验结果的影响因素进行了分析，提出了一些修正的方法［5－8］，而数据处理中剪切面面积变化对抗剪强度的影响很少考虑［9］。为揭示剪切面面积对抗剪强度的影响程度，提出改进直剪试验强度计算方法，本研究重新建立数学模型，在土样剪切破坏理论的基础上，推导出了抗剪强度与剪切面面积之间的关系，并且通过对比试验分析研究了改进后计算方法对抗剪强度的计算精度。

1 现行抗剪强度计算方法及存在的问题

1．1 现行抗剪强度计算方法

在直剪试验中，通常采用4个试样，分别在不同的垂直压力（通常取100、200、300、400kPa）下，施加水平剪切力进行剪切，求得破坏时的剪应力，然后根据库伦定律确定土的黏聚力和内摩擦角2个抗剪强度指 标。其试验原理如图1所示。

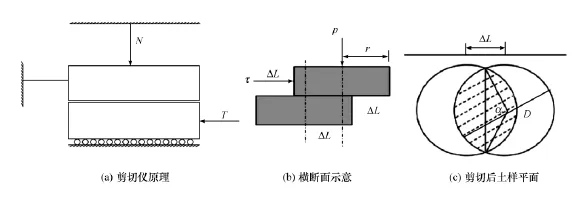
图1 常规直剪试验原理示意图

现行的计算方法认为土样的剪切破坏面面积为试样的横截面面积A，即：其中：D为试样的直径。并据此计算作用于土样上的剪应力τ和正应力σ分别为：

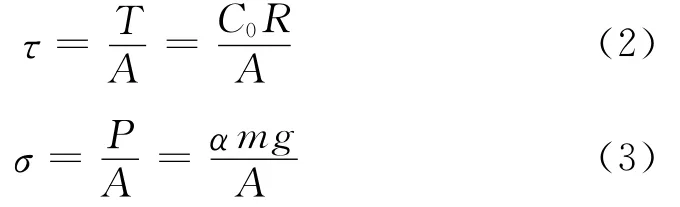
式中：C0为测力环系数；R为某荷重相应的百分表读数，0．01mm；P为垂直荷载，kN；m为砝码质量，kg；g为重力加速度，N／kg；α为直剪仪荷载传递系数。

根据不同σ作用下试样破坏时对应的τ及库伦原理（τ＝σtanφ＋c）确定土样的抗剪强度指标（内摩擦角φ和黏聚力c）。

1．2 现行抗剪强度计算中存在的主要问题

现行直剪试验抗剪强度计算中没有考虑剪切面积A的变化对抗剪强度的影响。不考虑剪切面面积变化影响将导致计算中出现2个方面问题：一是直接剪切试验中试样破坏时对应的正应力并非试验开始时设定的正应力，而是随实际的剪切面不断减小，正应力逐渐增大；二是在直接剪切试验中试样破坏时对应的剪应力并不是推力T除以试样截面积，而是剪切盒上下盒土样的接触面，如图1（c）所示。由于上述问题导致计算得到的试验结果存在较大误差，偏离了土样的真实强度。

2 剪切面面积的改进算法

2．1 考虑剪切位移且剪切面简化为平面时的面积计算方法

直剪试验实际剪切面的平面如图1（c）所示，图中阴影部分为剪切破坏时有效的剪切面积。考虑剪切位移且剪切面简化为平面时的面积计算方法（以下简称算法一）如下述。

实际剪切面积计算简图如图2所示。

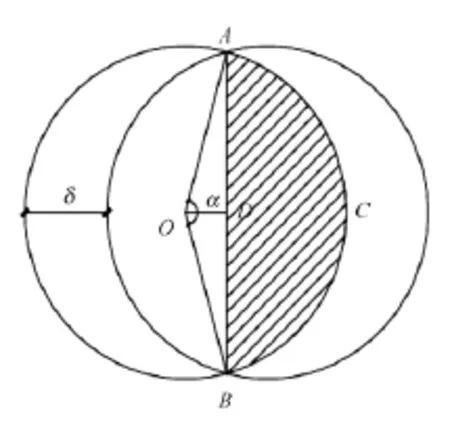
图2 剪切面为平面时的计算简图

由图2可知：如果剪切位移为δ，则

从而阴影部分区域ABDC部分面积S为

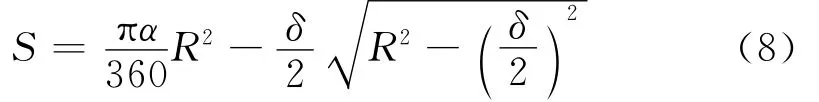
故真实剪切面的面积Ae为

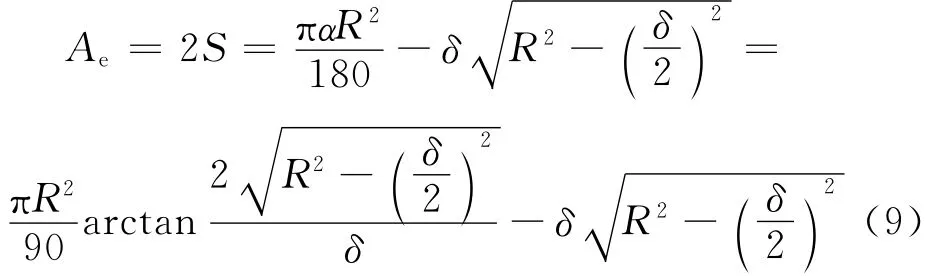
式中：R为量力环半径，mm；δ为为土体破坏时的剪切位移，mm。

2．2 考虑正应力偏心引起的剪切面起伏的面积计算方法

大量的试验表明，由于剪切过程中只有上盒或下盒在水平推力下移动，对应的下盒或上盒是固定的，加之剪切过程中竖向加载位置也没有随剪切面的变化而调整，导致剪切开始后，在试样的加载面上就开始出现偏心加载的情况，如图1（b）所示。且随着剪切位移的增加，偏心距也随之增大，造成试样剪切过程中的实际剪切面并非是平面，而是起伏曲面，如图3所示。

图3 应力偏心造成的实际剪切面

考虑正应力偏心引起的剪切面起伏的面积计算方法（以下简称方法二）为：试样剪切方向尺寸为b，若剪切位移为δ，波形面的起伏都为a，建立简化计算模型如图4所示。

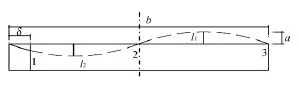
图4 波形剪切面面计算模型

作出波形线辅助计算圆如图5所示（图中D为辅助圆直径）。根据几何关系有：

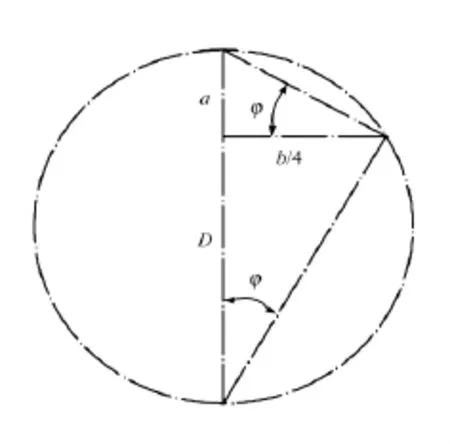
图5 辅助计算圆

2－3段的曲线长度l1为

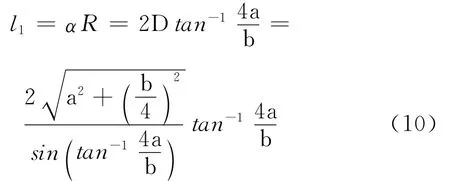
同理，1－2段的曲线长度l2为

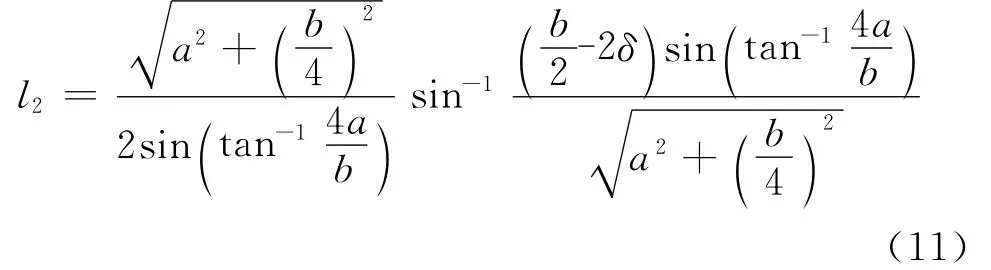
其中：根据试验破坏准则及试样尺寸，在大型直剪试验中δ＜b／4。

设想将图3（b）中的剪切面拉直，则可以得到如图6所示的计算简图。图6中阴影部分面积即为实际剪切曲面的面积。

图6 波形起伏面计算简图

此时土样受到的剪应力将沿着应力偏心造成的实际剪切面分布，正应力将沿着图4中2－3曲面的水平投影面分布，即分布面积大小为剪切面简化为平面时的面积。而阴影部分的面积As为

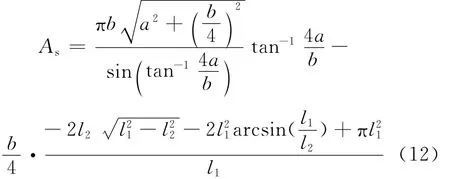
因此，正应力σ与剪应力τ计算公式分别为：

此计算方法中，准确测得剪切位移是计算的关键。为了精确测量试验过程中剪切位移，本研究对直剪仪进行了改进，加装了位移计和动态电阻应变测量系统，如图7所示。动态电阻应变仪接收位移计传入的信号，可以准确显示出位移计读数，进而快速准确得到剪切位移。

图7 剪切位移测量装置

2．3 考虑颗粒组成造成的剪切面粗糙度的剪切面面积计算方法

由于试样颗粒组成不同，在剪切过程中，土颗粒发生翻滚、切断和旋转等，实际土样的剪切面并非光滑的平面，如图8所示。

图8 剪切过程中的土颗粒运动

考虑颗粒组成造成的剪切面粗糙后的剪切面面积计算方法（以下简称方法三）：根据直剪试验后对剪切面的量测，可得到剪切面的起伏数据，再通过图形软件surfer进行数据加密，利用加密后的数据绘制得到剪切面的真实起伏特征，如图9所示。

由于真实剪切面具有分形特征，因此，真实剪切面面积的计算已无法通过简单的数学方法予以计算，但可以通过剪切面的起伏特征，将加密后的测量结果，导入Matlab等数学软件进行分析和处理，利用相似性原理，设定计算精度，计算剪切面的面积，该计算过程较为复杂。

3 剪切面面积对抗剪强度的影响分析

从理论分析的角度而言，将剪切面简化为平面时的面积计算方法简单、推导过程简单易懂，但是仅仅是考虑了剪切位移对于抗剪强度的影响。

图9 剪切面起伏特征的数值模拟

考虑正应力偏心引起的剪切面起伏的面积计算方法，简化后的剪切面形状与实际情况相近，计算时考虑了剪切面起伏和剪切位移对于抗剪强度的影响，较将剪切面直接按平面计算时精度要高。

考虑颗粒组成造成的剪切面粗糙度对剪切面计算方法更加接近于土样破坏时的真实情况，计算精度最高。但是由于该计算方法依托于Matlab计算软件，需要获取剪切面各点坐标，而剪切面各点坐标获取较繁琐，不利于工程实际的运用。

上述3种计算方法对计算结果的影响程度是不同的，同时考虑剪切试验结束后，剪切面能够上下分离，在黏土中掺加20%的天然砂，并进行击实试验，按照最佳含水率和96%的压实度，采用静力压载，一次成型的试件制作方法制作剪切试样，然后进行直接剪切试验，分析各种计算方法对于抗剪强度的影响。

3．1 方法一与现行计算方法计算结果的对比

由现行计算方法与方法一计算结果的对比如表1所示。表中的剪切位移分别为不同正应力下试样破坏时对应的剪切位移；正应力与剪应力是按照现行计算方法计算结果，实际正应力与剪应力是改进算法的计算结果。

表1 方法一与现行方法计算结果对比

由表1可知：随着正应力的增加剪切位移随之增大，而有效剪切面面积随之减小。当剪切位移达到3．79mm（约为试样直径的6．13%）时，剪应力增大8．47%；当剪切位移达到5．16mm（约为试样直径的8．35%）时，剪应力增大11．9%。计算结果与徐志伟等［10］提出的对于圆形土样，只要剪切位移不超过试样直径的7．725%，近似计算的剪切应力误差不会超过10%的结论相一致。

根据直剪试验原理，绘制剪切曲线如图10所示。由图10可以得到考虑剪切位移时试样的抗剪强度，与现行计算方法相比，黏聚力增加了2．15%，内摩擦角增加了1．76%。抗剪强度计算结果与詹金林［11］等验证的纯土样按现行算法低估了土体的抗剪强度指标的结论基本一致。

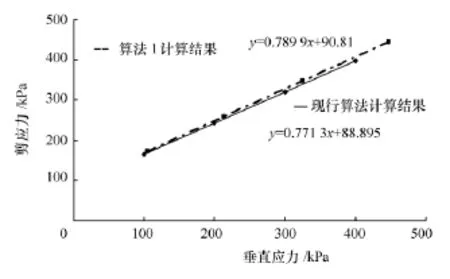
图10 算法一的抗剪强度曲线

3．2 方法二与现行计算方法计算结果的对比

方法二与现行抗剪强度计算方法计算结果对比如表2所示。

表2 方法二与现行方法计算结果对比

从表2的对比分析可知：作用于剪切面上的正应力及剪应力较现行计算方法均有较大的增加，正应力及剪应力的增加幅度均随着设定正应力的增加而增加，正应力增加幅度略大于剪应力增加幅度，剪应力增加的最大幅度为7．14%，正应力增加幅度达18．92%。

算法2的剪切曲线如图11所示。由图11的对比曲线可知，算法二得到的内摩擦角与现行算法相比减小了5．52%，黏聚力减小4．11%。说明考虑应力偏心等影响时，试样的实际强度小于现行规范的试验结果。

3．3 方法三与现行计算方法计算结果对比分析

考虑剪切面粗糙度并利用Surfer和Matlab软件计算剪切面的面积。利用Matlab计算所得的剪切面面积如表3所示，强度曲线如图12所示。

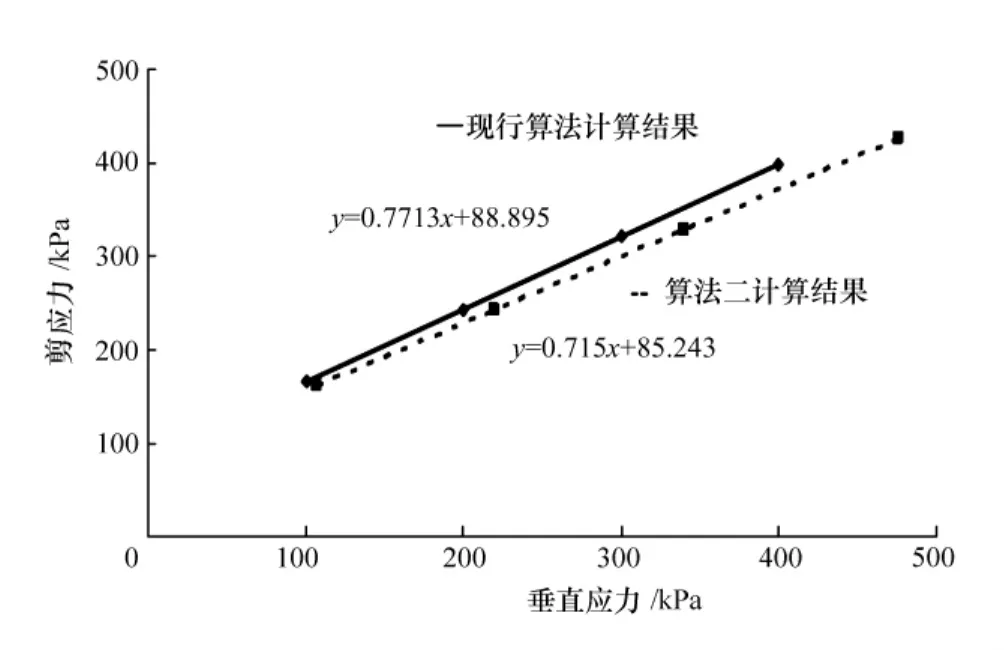
图11 算法二的抗剪强度曲线

表3 方法三（含砂量20%土）直剪试验抗剪强度

由表3的对比可见，考虑剪切面粗糙度计算时，计算结果相比现行计算方法正应力变大，剪应力减少，剪应力最大减小10．71%，正应力最大增加11．9%。

由图12可得，按照改进后算法计算，黏聚力较现有算法增加6．36%，而内摩擦角减小18．99%，结果与魏汝龙［12］、殷春娟等［13］的研究结果基本一致，说明按照现行计算方法高估了土的抗剪强度，将会影响实际工程的安全性。

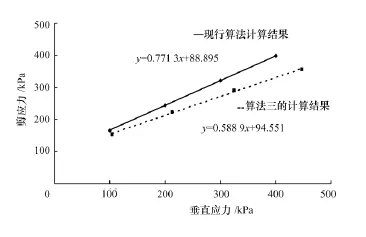
图12 算法三的抗剪强度曲线

3．4 各种计算方法计算结果对比分析

由上述3种改进的强度计算方法与现行抗剪强度计算方计算结果的对比分析，现行计算方法与考虑剪切位移并将剪切面为平面时的计算结果，均大于考虑正应力偏心及颗粒按照其余2种算法计算，其中改进算法一仅是考虑了剪切位移，剪切面仍简化为平面，但根据现有的研究及试验实际情况可知，实际剪切面并非是平面。另外，现有的研究成果大多表明直剪试验结果较三轴剪切试验结果偏大。因此改进算法二及算法三的试验结果应更接近于试样的真实强度。

由算法二及算法三的对比可知，应用Matlab等数学软件，根据剪切面起伏特征量测数据计算剪切面面积的计算结果应该更加接近试样的真实强度，但实际应用中获取剪切面各点准确坐标难度较大，表征各点起伏的坐标测量存在较大的误差。因此，基于Matlab软件的强度计算结果并不是非常准确。算法二也需要在试验中测量试样剪切后的起伏特征，因此，其应用范围也局限于剪切后剪切面能够分开的试样。

基于上述情况，若无法实现剪切面起伏特征的量测时，建议在现有计算方法的基础上，对抗剪强度指标中的内摩擦角进行一定的折减，折减率可取10%～15%，试样最大颗粒越大，折减系数越大，以使直剪试验的试验结果更接近于土体的真实强度。当然，随着试验设备的改进、数字影像及计算机仿真技术的发展，通过数字影像技术或仿真快速准确获取剪切面的起伏特征，并利用Matlab等数学软件分析剪切面，得到试样的真实强度一定能够实现。

4 结论与展望

本研究结果表明：

（1）现行直剪试验抗剪强度计算方法，虽然计算方法简单，但是却忽略了剪切面面积、剪切面起伏等对抗剪强度的影响，使得直剪试验数据结果偏离试样的真实强度；

（2）考虑剪切位移、但仍将剪切面简化为平面时，抗剪强度的计算结果较现行规范计算方法得到的计算结果略大，但仍没有考虑正应力偏心及颗粒运动的影响，计算结果同样偏离试样的真实强度；

（3）考虑正应力偏心及颗粒运动引起的剪切面起伏的面积及抗剪强度的计算方法，计算结果更加接近土样强度真实值，但实际应用中较难获得剪切面的起伏特征；

（4）结合各种计算方法及现有的研究成果，在无法获得剪切面起伏特征时，建议按现行规范的抗剪强度计算结果，对抗剪强度指标进行一定的折减。

直剪试验在实践工程中广泛应用，通过研究提出抗剪强度计算方法改进，可使得试验结果更接近试样的真实强度，具有重要的工程应用价值。目前的研究限于仪器设备及量测手段限制，实际应用困难，在进一步的研究中，可重点进行直剪试验仪器设备的改进，避免正应力的偏心及剪切过程中保持正应力的恒定。同时，加强交叉学科的技术应用，将先进的数字影像技术、计算机仿真技术与岩土测试技术相结合，以推动岩土测试技术的发展，使得试验结果更接近试样的真实值。

（References）

［1］董云，柴贺军．土石混合料室内大型直剪试验的改进研究［J］．岩土工程学报，2005，27（11）：1329－1333．

［2］徐进，刘建锋，高春玉，等．新型粗粒土直剪试验机研制［J］．四川大学学报：工程科学版，2008，40（4）：12－16．

［3］Jewell R A．Direct shear tests on sand［J］．Geotechnique，1989，39（2）：309－322．

［4］Jewell R A，Wroth C P．Direct shear tests on reinforced sand［J］．Geotechnique，1987，37（1）：53－68．

［5］张敏江，郭尧，张丽萍，等．直剪试验中对土抗剪强度的一种修正方法［J］．沈阳建筑大学学报：自然科学版，2005（2）：96－98．

［6］刘天韵．直剪试验固结快剪强度指标影响因素探讨［J］．中国港湾建设，2009（6）：32－34．

［7］薛鹏涛，雷金山，肖立．土工直剪试验的最小二乘法拟合［J］．中外公路，2007（5）：41－44．

［8］邓华锋，原先凡，李建林，等．土石混合体直剪试验的破坏特征及抗剪强度取值方法研究［J］．岩石力学与工程学报，2013（增刊2）：4065－4072．

［9］刘海波，张丽华，林大超，等．直剪试验有效剪切面积动态变化的改进计算［J］．沈阳建筑大学学报：自然科学版，2010（3）：503－506．

［10］徐志伟，周国庆，刘志强，等．直剪试验的面积校正方法及误差分析［J］．中国矿业大学学报，2007，36（5）：658－662．

［11］詹金林，雷国辉，施建勇，等．有效剪切面积对直剪试验结果的影响分析［J］．河海大学学报，2007，35（2）：213－216．

［12］魏汝龙．三轴和直剪试验的固结快剪指标［J］．大坝观测与土工测试，1998（1）：25－26，43．

［13］殷春娟，赵云祥．镇江市下蜀黄土三轴与直剪试验强度指标关系［J］．西部探矿工程，2007（10）：55－57．

Study on effect of calculation methods of shearing area on shear strength in direct shear test

Dong Yun1，Wang Yongcun2
（1．Architectural and Civil Engineering Institute，Huaiyin Institute of Technology，Huaian 223001，China；2．Architectural and Civil Engineering Institute，Chongqing Jiaotong University，Chongqing 400074，China）

Direct shear test is broadly used to get the strength of soil，joints，and specific material in the field of geotechnical engineering because of its simple structure and operation．But the current direct shear strength calculation does not concern on the variation of the shearing surface during the test，has no regard for the effect of the shearing area on the shear strength，so the test result is not the really strength of the samples．To analyse the effect of the shearing surface on the direct shear strength，three different calculation methods of shear surface and its effect on the shear strength are put forward based on the new mathematical model and a large number of experiments with improving the direct shear apparatus，the new calculation method can make the result more accuracy and closer to the really shear strength of the samples．

direct shear test；shearing area；angle of internal friction；cohesion

TU 411．7

B

1002－4956（2015）3－0057－06

2014－07－09 修改日期：2014－09－03

江苏省高校自然科学研究项目（10KJB170002）；国家级大学生实践创新训练计划项目（2013－JSSPITP－2559）

董云（1974—），男，江苏泗阳，博士，副教授，副院长，主要从事道路工程、岩土工程的教学与研究．