Heisenberg群上拟线性椭圆方程解的多重性

贾 高, 郭露倩, 张龙杰

(上海理工大学理学院,上海 200093)

Heisenberg群上拟线性椭圆方程解的多重性

贾 高, 郭露倩, 张龙杰

(上海理工大学理学院,上海 200093)

在Heisenberg群上研究一类拟线性椭圆方程边值问题解的多重性.在全空间中,假设方程的主导系数及导数有界,而方程的非线性项具有超线性增长.由于在该假设下,方程所对应的泛函是连续的,但没有可微性,因此必须使用不光滑临界点理论.首先,介绍不光滑临界点理论中的弱斜率、临界点、(PS)c条件等概念和相关的基本引理;其次,研究泛函的临界点的性质,利用非线性泛函理论、Fatou引理、Lebesgue控制收敛定理和Brezis-Browder定理证明(PS)c序列的强收敛性质;最后,借助推广的山路引理得到该边值问题具有无穷多个解,且这些解是彼此分离的.

拟线性椭圆方程;不可微泛函;不光滑临界点理论;Heisenberg群

近年来,在欧氏空间中,关于拟线性椭圆方程解的存在性和多重性问题已有许多学者进行研究[1-5],在Heisenberg群上关于半线性或拟线性次椭圆方程的研究也主要集中于对单个解的存在性[6-9].本文在Heisenberg群上研究一类拟线性椭圆方程解的多重性.

1 问题的提出

所谓Heisenberg群 HHN是指在瓗N×瓗N×瓗上定义如下的群运算式中,◦表示通常瓗N中的内积,则这个运算赋予 HHN李群结构.

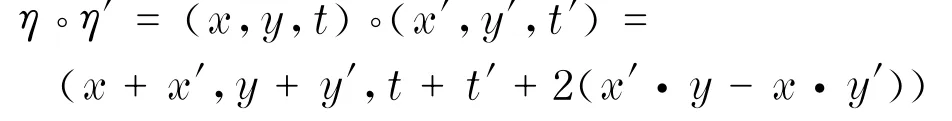
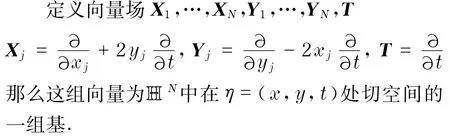
定义1 Heisenberg群上Laplace算子被定义

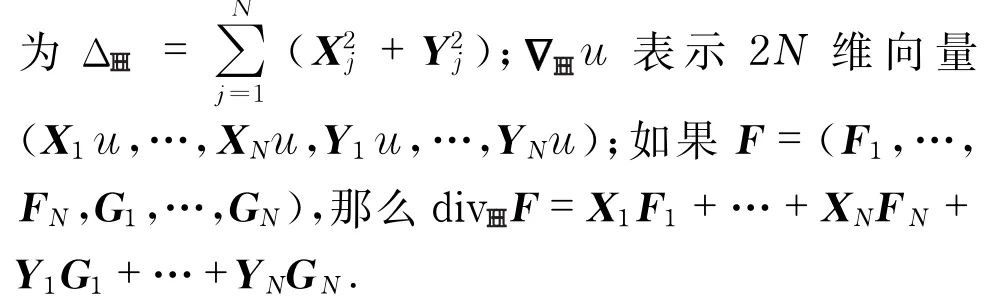
本文研究下面问题解的存在性和多重性.

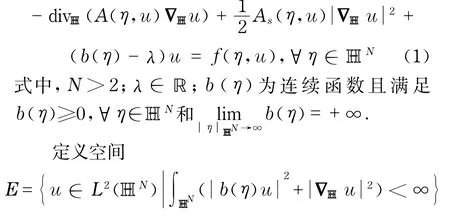
利用变分法来研究式(1),寻求其弱解等价于找如下泛函I:E→瓗的临界点

定义2 称u是泛函I的临界点,如果u∈E,使得〈I′(u),h〉=0,∀h∈E∩L∞( HHN).

下面给出如下基本条件:

a.A(·,·): HHN×瓗→瓗满足对于每个s∈瓗,A(η,s)关于η是可测的,对几乎所有的η∈ HHN, A(η,s)关于s是属于C1的;

b.存在0＜α＜β＜+∞,使得α≤A(η,s)≤β, |As(η,s)|≤β,a.e.η∈ HHN和∀s∈瓗;

本文的主要结论是:

定理1 若A(η,s)和f(η,s)分别满足条件a—d和条件e—f,则存在序列{un}⊂E∩L∞( HHN)是式(1)的弱解,且有I(un)→+∞.

2 预备知识和基本引理

为了得到定理1,建立下列引理.首先介绍引理1(参考文献[10]中的定理1.4),它是C1泛函经典结论的推广(参考文献[13]中的定理9.12).

引理1 设X是无限维Banach空间,f:X→瓗为连续的偶泛函,且对任意c∈瓗,I满足(PS)c条件.更进一步假设:

a.对于任意有限维子空间W⊂E,∃瓗＞0,使得∀u∈W:u=瓗⇒f(u)≤f(0);

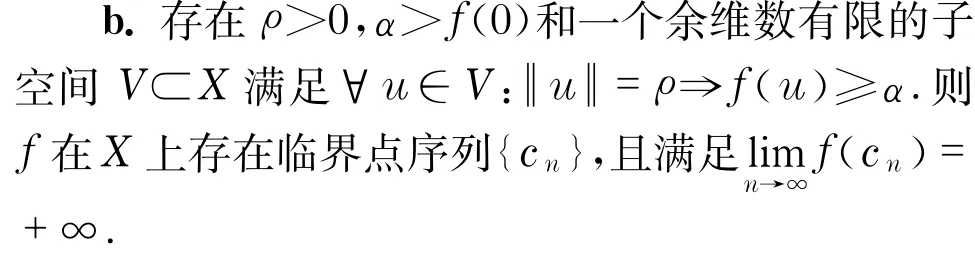
为了证明泛函I满足(PS)c条件,还需要引入(C-P-S)c条件的定义.

引理2 设c为一实数,若I满足(C-P-S)c条件,则I满足(PS)c条件.

证明方法是基本的,可以参考文献[11],这里

〈I′(u),h〉=0,∀h∈E∩L∞( HHN)(7)即u是I的一个临界点.

证明方法可参考文献[10]中的引理2.3,此处省略.

下面的引理是Brezis-Browder定理[9]的向量形式,其证明可参考文献[8].

3 定理1的证明

容易验证泛函I是连续且为偶泛函.进一步由引理2,对于∀c∈瓗,泛函I满足(PS)c条件.

首先,证明泛函I满足引理1的假设a.

设W是空间E的有限维子空间,且u∈W使得I(u)≥0.于是由假设b得到

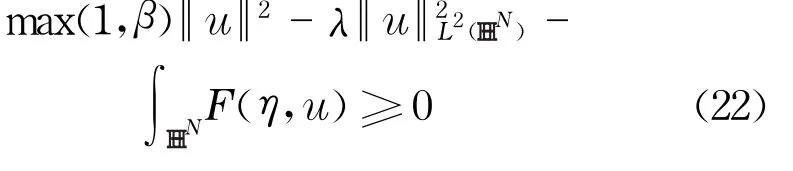
由条件e和条件f,存在m(η)∈L∞( HHN)满足m (η)＞0,a.e.η∈ HHN和一个正常数C,使得

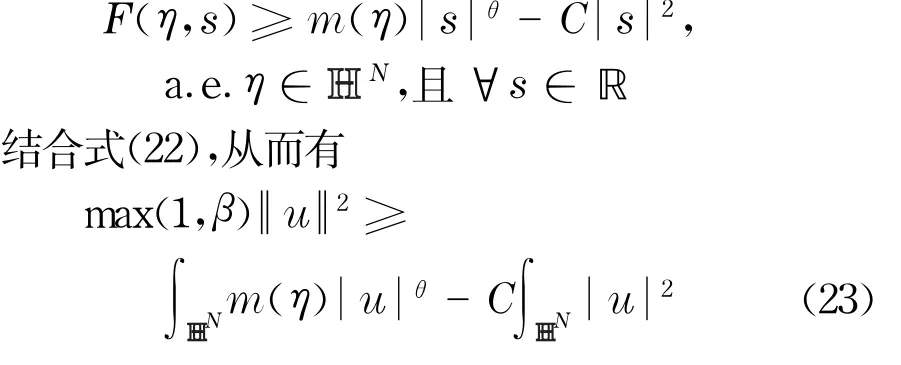
因为θ＞2,故集合{u∈W,I(u)≥0}在E上有界,说明引理1的假设a成立.

其次,证明泛函I满足引理1的假设b.

由条件b和条件f,对u∈E,有

[1] Aouaoui S.Multiplicity of solutions for quasilinear elliptic equations in瓗N[J].Journal of Mathematical Analysis and Applications,2010,370(2):639-648.

[2] Gazzola F.Positive solutions of critical quasilinear elliptic problems in general domains[J].Abstract and Applied Analysis,1998,3(1/2):65-84.

[3] Salvatore A.Some multiplicity results for a superlinear elliptic problem in瓗N[J].Topological Methods in Nonlinear Analysis,2003,21:29-39.

[4] 赵美玲,贾高.加权Sobolev空间中奇异拟线性椭圆方程共振问题[J].上海理工大学学报,2012,34(6):598-603.

[5] 刘向平,章国庆.带非线性边界的p-Laplacian问题的多重解[J].上海理工大学学报,2013,35(5):449-451.

[6] Garofalo N,Lanconelli E.Existence and nonexistence results for semilinear equations on the Heisenberg group[J]. Indiana University Mathematical Journal,1992,41(1): 71-98.

[7] Niu PC.Nonexistence for semilinear equations and systems in the Heisenberg group[J].Journal of Mathematical Analysis and Applications,1999,240(1):47-59.

[8] Squassina M.Existence of multiple solutions for quasilinear diagonal elliptic systems[J].Electronic Journal of Differential Equations,1999(14):1-12.

[9] Brezis H,Browder F E.Sur une propriata des espaces de Sobolev[J].Comptes Rendus Mathématique Académie des Sciences Paris A-B,1978,287(1): 113-115.

[10] Canino A.Multiplicity of solutions for quasilinear elliptic equations[J].Topological Methods in Nonlinear Analysis,1995,6(2):357-370.

[11] Douik H.Variational methods in nonsmooth analysis and quasilinear equations[D].Germany,North Rhine Westphalia:Aachen University,2003.

[12] Ladyaenskaya O A,Uralceva N N.Linear and quasilinear elliptic equations[M].New York:Academic Press,1968.

[13] Rabinowttz P H.Minimax methods in critical point theory with applications to differential equations[M]. Providence:American Mathematical Society,1986.

(编辑:董 伟)

Multiplicity of Solutions of Quasilinear Elliptic Equations on Heisenberg Group

JIAGao, GUOLuqian, ZHANGLongjie
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

The multiplicity of solutions for a class of quasilinear elliptic boundary value problems on the Heisenberg group was concerned.In the whole space,the main coefficients and their derivatives were assumed to be bounded,and the nonlinear term satisfies superlinear growth conditions.Under the above assumptions,the functional is continuous but not differentiable in the whole space.So,the nonsmooth critical point theory should be applied.The concepts about weak slope,critical point,(PS)cconditions and some fundamental lemmas in the nonsmooth critical point theory were introduced.The properties of the critical point of the functional were analysed.The strong convergence of the(PS)csequences was proved by using nonlinear functional theory,Fatou’s lemma,Lebesgue’s dominated convergence theorem and Brezis-Browder theorem.Moreover,by virtue of the generalized Mountain Pass lemma,the existence of infinite weak solutions of the boundary value problem was confirmed and these solutions are separable from one another.

quasilinear elliptic equation;nondifferentiable functional;nonsmooth critical point theory;Heisenberg group

O 175.25

A

1007-6735(2015)03-0210-05

10.13255/j.cnki.jusst.2015.03.002

2014-03-13

国家自然科学基金资助项目(11171220);沪江基金资助项目(B14005)

贾 高(1960-),男,教授.研究方向:非线性分析及应用.E-mail:gaojia89@163.com