负荷模型对仿真计算的影响

徐宏雷，霍锦霞，李学仕

(1.甘肃省电力公司调控中心，甘肃 兰州 730050；2.兰州城市学院，甘肃 兰州 730050)

负荷模型对仿真计算的影响

徐宏雷1，霍锦霞2，李学仕2

(1.甘肃省电力公司调控中心，甘肃 兰州 730050；2.兰州城市学院，甘肃 兰州 730050)

首先对静态负荷模型和综合负荷模型的数学模型进行了介绍，然后基于西北电网的计算数据包进行了稳定计算。计算采用相同的静态负荷模型和综合负荷模型分别在两种故障条件下进行了计算，分别得到了两种截然不同的计算结果。给出了应重视电网负荷的建模工作，并选择正确的负荷模型的建议。

负荷模型；电力系统仿真；稳定计算；断面极限

1 引言

电力系统仿真广泛用于电网运行和规划中，电力系统元件的模型建立是仿真计算环节中至关重要的一步。计算结果与实际情况的吻合程度取决于所采用的模型及其参数的准确性。同步发电机组模型及输电线路模型已较为成熟，相对而言，负荷模型的发展较为落后，成为影响计算精度的因素之一，导致仿真结果与实测波形差别较大。

随着电网规模不断增大，各电网大区联网工程建设逐渐开展，电网发展方向向着高电压等级、高输电能力发展。电力系统动态稳定问题和暂态稳定问题变得更加复杂，稳定性问题突出，负荷模型的不同对电力系统仿真计算结果的影响越来越突大。大量的仿真计算和试验结果表明：负荷模型对潮流、短路电流、暂态稳定、动态稳定以及电压稳定的仿真计算结果影响越来越大。

2 负荷模型分类

负荷随电压和频率的变化而变化的特性称为负荷特性，用于描述负荷特性的数学方程称为负荷模型。许多专家和学者对负荷模型的分类进行了研究[1-2]，从是否考虑电网状态暂态过程的角度来看，负荷模型分为静态负荷模型和动态负荷模型。

静态负荷模型相当较为简单，没有考虑时间对系统特性因素的影响，一般用代数方程描述。动态负荷模型则考虑了时间对系统特性因素的影响，一般用微分方程或者差分方程描述。

3 静态负荷模型

3.1 幂函数静态负荷模型

幂函数模型负荷模型主要适用于电网电压较为稳定系统中，电压只是在较小范围内波动，通常情况不超过额定电压的10%。其模型数学表现形式如式(1)所示。

(1)

P0、Q0、U0和ω0分别表示系统稳态运行时有功功率、无功功率、电压和角频率的值，亦即初始值。而P、Q、U和ω则为系统实际运行时负荷吸收的有功功率、无功功率、负荷母线电压幅值和角率，为随频率、电压波动的变化值。Pu、Qu为负荷有功、无功的电压静态特征系数，Pf、Qf为负荷有功、无功的频率静态特征系数。

3.2 多项式静态负荷模型

不同类型的负荷消耗的功率大小随端点电压的变化而变化，根据这一特性可将电力系统负荷的类型分为三种：恒阻抗负荷、恒电流负荷和恒功率负荷，也即是ZIP负荷模型。在实际电力系统中，用电设备的多样性决定了负荷组成的复杂性，通常按照这三类负荷的不同比例组合构成的综合负荷来描述各种负荷的特性。其模型如式(2)所示。

(2)

式(2)中：Fp为有功频率指数;Fq为无功频率指数；p1、p2、p3分别表示恒阻抗负荷、恒电流负荷和恒功率负荷在有功功率中所占的比例；系数q1、q2、q3分别表示恒阻抗负荷、恒电流负荷和恒功率负荷在无功功率中所占的比例。并且有如式(3)的关系。

(3)

4 综合负荷模型

实际电力系统运行中对电网的动态特性影响较大的负荷主要是感应电动机负荷，且感应电动机负荷占总负荷达到一半以上，暂态计算条件下必须考虑负荷的动态特性。在大区电网功率振荡研究、发电机自励磁及同步扭振、负荷电压稳定性研究中，负荷的动态过程是一个重要的考虑内容。为了更接近电网运行实际，学者对多种负荷模型进行了研究，并对静态负荷模型进行了改进，提出了含有电动机模型的综合负荷模型。综合负荷模型由静态的恒阻抗负荷、恒电流负荷和恒功率负荷与感应电动机负荷并联组成，如图1所示。

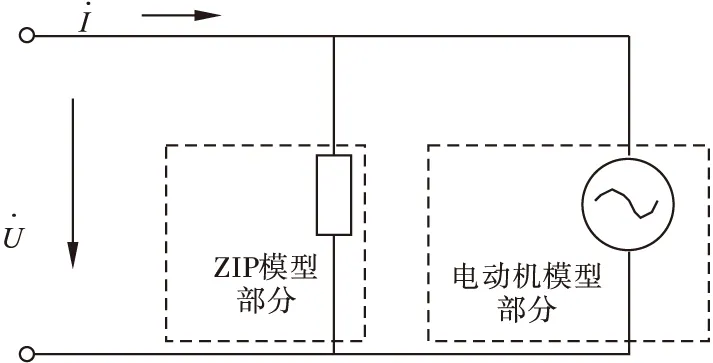
图1 综合负荷模型结构简图

其中电动机模型部分为三阶感应电动机，其物理结构简化结构可用图2表示。

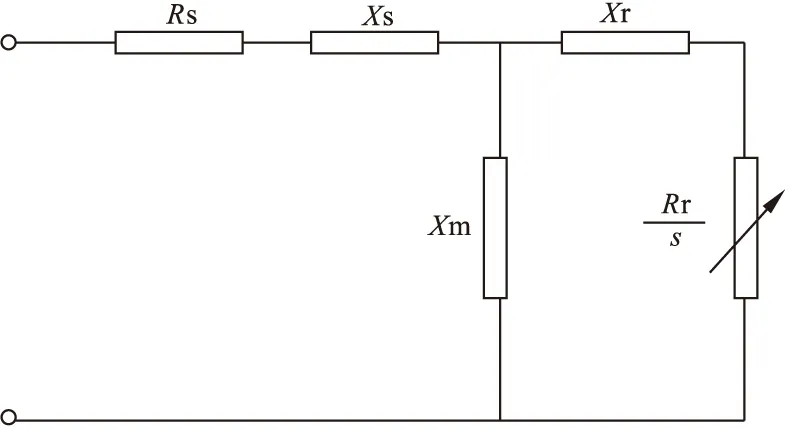
图2 电动机负荷模型部分结构简图

其数学模型为：

(4)

式中Rs、Xs、Rr、Xr、Xm分别是等值电动机的定子电阻、定子漏抗、转子电阻、转子漏抗与电动机激磁电抗，H为转子的惯性时间常数，Tm为机械负载力矩，Te为电力矩。

5 不同负荷模型对仿真计算的影响

实际电网中每天的电力负荷是在不断变化着的，每种负荷的构成也是在变化的。因此，采用一种能够具有代表性模型来表示电力负荷的特性，就具有十分重要的意义。下面分别就静态负荷模型和综合负荷模型分别进行暂稳计算，分析两种负荷的特性对计算结果的影响程度。

采用2014年西北电网计算数据包，分别采用静态负荷和综合负荷进行计算。其中静态负荷模型参数采用多项式负荷模型，具体参数如下：p1=1.33,p2=-1.86,p3=1.53,Fq=2,q1=6.66,q2=-9.32,q3=3.66,Fp=1。综合负荷模型参数具体如下：Rs=0.02，Xs=0.18，Rr=0.02，Xr=0.12，Xm=3.5，H=2。

5.1 750kV河武双回同杆异名相故障计算

分别采用如上静态负荷模型和综合负荷模型，对甘肃电网750kV河武双回同杆异名相故障重合不成功计算。计算采用故障后0.3s切除风电2500MW、切除负荷40MW的措施，计算时间40s，计算结果如图3所示。

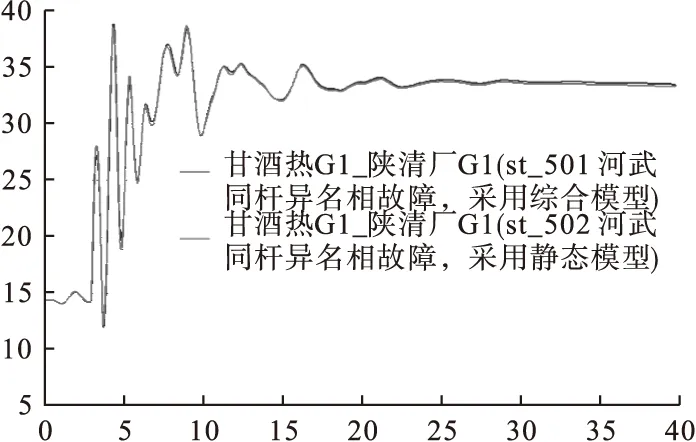
图3 河武双回同杆异名相故障重合不成功曲线对比

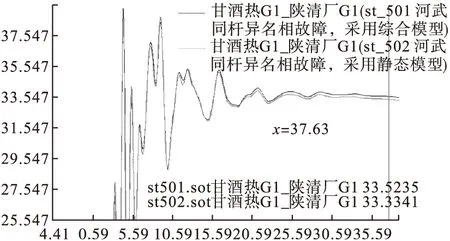
图4 对比曲线局部放大

由图4可以看出，在上述计算边界条件下两种负荷模型的稳定计算结果较为相似，省际间发电机功角振荡相差0.1894°。

5.2 酒泉单主变故障计算

采用如上负荷模型，在同一潮流作业基础上对甘肃电网750kV酒泉变单主变330kV侧三永故障故障跳主变进行计算。计算采用故障后0.3s切除风电790MW的措施，计算时间30s，计算结果如图5所示。 由图5可见，采用静态负荷模型与综合负荷模型的计算结果在故障前完全重合，在3.7s故障后第一摆最大值处产生差别，之后差别更为明显。采用静态负荷模型的计算，省际间发电机功角差最大值已经大于500°，可判为系统失稳，需进一步下调断面潮流，用以保证系统稳定；而采用综合负荷模型计算，功角收敛至正常范围，可判为系统稳定。

图5 750kV酒泉主变330kV侧三永跳主变曲线对比

6 结语

通过对相同的静态负荷模型参数和综合负荷模型参数在两种不同故障条件下的计算结果进行对比，可以看出，在电网稳定计算中，稳定计算结果可能较为相似，也有可能截然不同，不同的计算条件可能导致造成完全不同的计算结果。专家和学者也就负荷建模方面做出了大量的研究[3-8]，因此，应十分重视电网负荷的建模工作，并选择正确的负荷模型，加强对负荷部分的组成及其数学模型进行分析，提高负荷模型的精准度，保证稳定计算结果的有效性。

[1] 张景超，鄢安河,张承学，等.电力系统负荷模型研究综述[J].继电器，2007，35(6)：83-88.

[2] 贺仁睦，周文.电力系统负荷模型的分类与综合[J].电力系统自动化，1999，23(19)：12-16.

[3] 鞠平，谢会玲，陈谦.电力负荷建模研究的发展趋势[J].电力系统自动化，2007，31(2)：1-4.

[4] 李培强，李欣然，林舜江.电力负荷建模研究述评[J].电力系统及其自动化学报，2008，20(5)：56-64.

[5] 鞠平.电力系统负荷建模理论与实践[J].电力系统自动化，1999，23(19)：1-7.

[6] 鞠平，赵夏阳.电力负荷模型可辨识性分析方法[J].电力系统自动化，1999，23(19)：29-33.

[7] 汤涌，张红斌，侯俊贤，等.负荷建模的基本原则和方法[J].电网技术，2007，31(4)：1-5.

[8] 张红斌，汤涌，张东霞，等.负荷建模技术的研究现状与未来发展方向[J].电网技术，2007，31(4)：6-10.

The Effect of the Load Model on the Simulation Calculation

XUHong-lei1,HUOJin-xia2,LIXue-shi2

(1.Regulation and Control Centre of Gansu Power Company, Lanzhou 730050,China;2.Lanzhou City College,Lanzhou 730050,China)

First,present the mathematical models for the static load model and integrated load model,then carry out stability calculation based on computer packet of Northwest grid.The calculation,which adopted the same static load model and integrated load model,carried out calculations under two kinds of fault conditions,respectively get two entirely different calculation results.The paper gives out modeling work to pay attention to the electric network load and select correct load model suggestion.

load model;electric power system simulation;stability calculation;sectional limit

1004-289X(2015)02-0097-03

甘肃省城市发展研究院项目(2013-GSCFY-KJ04)

TM71

B

2014-11-14

徐宏雷(1979-)，男，硕士，工程师，主要从事电网运行控制、电网仿真计算方面的研究； 霍锦霞(1973-)，女，本科，副教授，主要从事数学教学、数学模型建模方面的研究； 李学仕(1967-)，女，硕士，讲师，主要从事数学教学、数学模型建模方面的研究。