基于振动信号分析的配电开关机械状态诊断系统

黄蓉，陈永往，陈立纯，郭谋发

(1.福州大学电气工程与自动化学院,福建 福州 350108；2.国网福建晋江市供电有限公司,福建 泉州 362200)

基于振动信号分析的配电开关机械状态诊断系统

黄蓉1，陈永往2，陈立纯2，郭谋发1

(1.福州大学电气工程与自动化学院,福建 福州 350108；2.国网福建晋江市供电有限公司,福建 泉州 362200)

配电开关的振动信号包含有丰富的开关机械状态信息，可以通过合理有效的方法提取振动信号特征量，作为配电开关机械状态诊断的依据。根据数据采集的功能需求，设计了基于LabVIEW的振动信号采集装置软硬件。利用经验模态分解(empirical mide decomposition，EMD)对振动信号进行时频分解，提取分解所得固有模态分量(intrinsic mode function，IMF)的样本熵作为特征量，最后通过模糊C-均值聚类(fuzzy C-means，FCM)进行机械状态诊断。通过实验，采集并分析了正常状态和典型故障状态下的配电开关振动信号，验证了基于振动信号分析的配电开关机械状态诊断系统的准确性和有效性。

配电开关；机械状态；振动信号；EMD；样本熵；FCM

1 引言

配电开关在配电网中具有控制和保护双重功能，配电开关故障可能引起严重的电网事故，大部分的配电开关故障都属于机械故障。配电开关机械状态诊断就是在状态监测的基础上对开关机械状态进行准确的诊断识别，从而合理地安排检修策略。

配电开关分、合闸过程中，操动机构内部各组件依序动作，形成激励源并由此产生振动信号，该信号包含有大量的开关机械状态信息，是典型的无规律、非平稳、时变信号。振动诊断法就是通过分析配电开关的振动信号，提取有效特征量，从而对其机械状态进行诊断识别的方法。振动诊断法具有可靠性和准确性，有利于实现对开关的非侵入式状态监测[1]。

目前，基于不同原理的配电开关状态监测方法的可靠性、普适性和经济性有待提高；以“事后检修”和“到期必修”为主的配电开关计划检修策略也不能够满足现代电网安全、可靠、经济运行的要求。建立在配电开关状态监测和状态诊断基础上的配电开关状态检修是当前先进的检修策略[1-2]。基于上述配电开关状态监测、检修现状，本文研制出一套基于振动信号分析的配电开关机械状态诊断系统，系统主要由振动信号采集装置和振动信号分析软件组成，包括信号采集、特征提取、状态诊断3部分功能。该系统能够准确诊断出配电开关的机械状态，为配电开关的状态检修提供可靠依据。

2 振动信号采集装置设计

配电开关振动信号采集装置主要由压电式加速度传感器、信号调理模块、数据采集卡和波形显示存储平台四部分组成。压电式加速度传感器将配电开关振动信号转化为电压信号；信号调理模块对信号进行分离、放大和抗混叠滤波处理，去除直流电压耦合信号；数据采集卡将模拟信号转换为数字信号，并通过USB接口将信号上传至上位机；波形显示存储平台完成对信号的显示和存储。

2.1 装置硬件设计

根据配电开关振动信号高频率、高强度冲击、有效信号时间短等特点，结合配电开关振动信号的振动频率范围与检测环境，选用输出阻抗低、抗扰能力强的LC0102T型压电式加速度传感器采集振动信号。该加速度传感器的频率响应范围为2～13000Hz，灵敏度为10mV/g，量程为500g，分辨率为0.004g。

采用LC0207型恒流源模块作为信号调理模块，为LC0102T型压电式加速度传感器提供18～30V、4mA的恒流电源，同时将LC0102T型压电式加速度传感器输出的叠加有直流信号的交流信号通过CR高通隔直输出。加速度传感器采集到的开关振动信号容易受到测试环境中的噪声及强磁等因素干扰，因此采用屏蔽同轴电缆连接传感器和恒流源模块。

配电开关分、合闸振动的有效信号持续时间通常只有数十到数百毫秒，要求数据采集卡具有较高的采样率和采样精度、较快的数据传输速度。综合考虑配电开关振动信号的特点和对其进行分析诊断所需达到的频谱范围，选用了美国国家仪器公司(National Instrument，NI)USB-6211型多功能数据采集卡，USB-6211具有16路16位模拟信号输入通道，2路16位模拟输出通道，总采样率为250kS/s；4路数字输入通道和4路数字输出通道。

2.2 装置软件设计

LabVIEW是目前应用较为广泛的图形化编程语言设计软件，具有操作简单灵活、数据显示清晰等特点，能够搭建良好的可视化人机交互平台[3]。系统以LabVIEW作为搭建波形显示存储平台的编程软件。

压电式加速度传感器采集到的配电开关分、合闸振动信号经由数据采集卡A/D采样后送入波形显示存储平台。在LabVIEW中采用DAQ助手.vi实现对数据采集卡的参数配置，其中包括采样通道、采样率和采样方式的设置。当从DAQ助手.vi读取的振动信号采样值超过阈值时，记录振动信号触发之前的4400个采样点和之后的41200个采样点，并以tdms文件格式储存振动信号波形，反之则重新检测振动信号。通过字符串的组合，tdms文件可以根据开关编号、位置编号和录波次数实现自动命名，开关编号和位置编号可由操作人员在显示界面中进行手动设置，录波次数编号则在系统完成一次录波操作后自动加1，具体流程如图2所示。显示界面能够显示出实时振动信号波形和上一次开关振动信号波形，如图2所示。

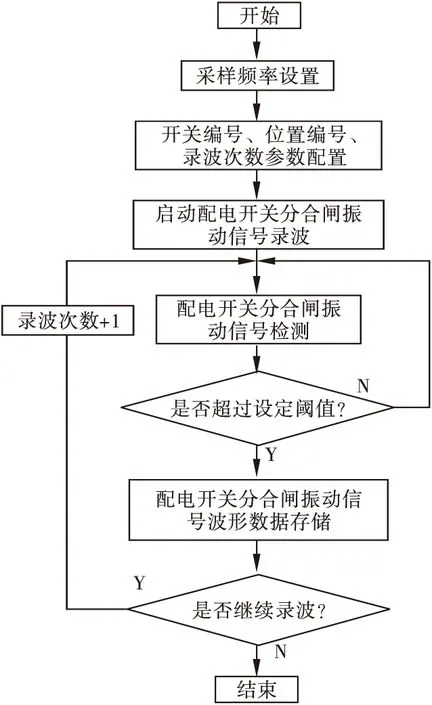
图1 波形显示存储平台软件流程图

配电开关振动信号采集装置还可以进行功能拓展，如采集配电开关分、合闸线圈电流、测量配电开关的开关量、开关行程等，作为配电开关机械状态诊断的辅助诊断信息。

3 振动信号分析原理与算法设计

配电开关振动信号分析软件主要对采集装置采集到的振动信号进行分析处理，提取能够表征配电开关机械状态信息的有效特征量作为状态诊断的依据。分析算法基于Matlab编程软件完成。

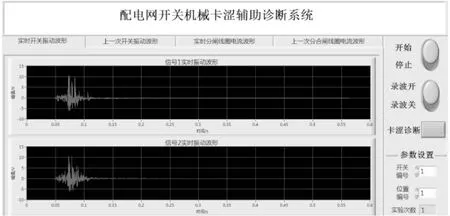
图2 波形显示存储平台显示界面图

按照以下步骤对配电开关的振动信号进行分析：

(1)在配电开关分、合闸振动信号进行分析诊断前，先对采集到的正常状态、故障状态下的波形信号进行截取处理，提取可供分析的有效部分。

(2)对经由步骤(1)截取得到的有效振动信号进行EMD，得到IMF。EMD根据振动信号序列自身的时间尺度特征将其自适应分解成有限个不同频率、不等带宽的IMF和一个残差之和[4-5]。与小波、小波包分解相比，EMD不存在预先选取最优基函数的问题，能够更好地表示出信号的局部特征，是处理非平稳、非线性信号的有效方法，适用于振动信号的时频分解。

(3)计算振动信号各阶IMF的样本熵，作为状态诊断的特征量。熵是表征系统不确定程度的函数，系统的状态发生变化时，其熵值也会发生改变。样本熵是在近似熵的基础上对其进行修正发展而来的，是一种将非线性数据序列量化为不计自身数据长度比较的统计量。样本熵还具有一定的抗噪声干扰能力，算法的计算精度和计算时间较近似熵有了很大的提高[6]。

(4)将振动信号的各阶IMF样本熵值构成的矩阵作为FCM的输入进行聚类，诊断出配电开关的机械状态。FCM是无监督模糊聚类方法中的一种，算法简单快速，具有比较直观的几何意义。利用FCM算法把n个振动信号向量xj(j=1,2,…,n)划分成c类模糊簇(2≤c≤n)，求取每类簇的聚类中心vi(i=1,2,…,c)，以使得目标函数尽量小为原则，将振动信号的特征数据点按一定的隶属度归于某一簇聚类中心[7]。

3.1 振动信号的时频分解

对振动信号进行EMD，得到的各阶IMF分别表示振动信号的一个内在特征振动形式，包含有实际物理意义[5]。IMF必须满足两个条件：①对于一列振动信号数据，极值点数目和零点数目必须相等或至多相差一点；②在振动信号上任意点，由局部极大值点构成的包络线和局部极小值点构成的包络线的平均值为零。

对振动信号进行时频分解的EMD算法的具体计算步骤如下[8-9]：

(1)计算振动信号S(t)的所有局部极值点。

(2)利用3次样条函数将振动信号的所有极大值点和所有极小值点分别拟合成数据的上包络线a0(t)和下包络线b0(t)。求出上、下包络线的均值m0(t)

m0(t)=[a0(t)+b0(t)]/2

(3)求出振动信号S(t)与上、下包络线的均值m0(t)的差，得到一个去掉低频的振动数据序列，记为h0(t)。

h0(t)=S(t)-m0(t)

(4)判断h0(t)是否满足①和②。若满足，则h0(t)为振动信号S(t)的一阶IMF；否则记h0(t)为S(t)，重复步骤(1)～(3)，直至得到表示振动信号S(t)中高频率分量的第一阶振动信号IMF，记为c1(t)。

(5)记r1(t)=S(t)-c1(t)为新的待分析信号，重复步骤(1)～(4)，得到第二阶IMF，记为c2(t)，此时余项为r2(t)=S(t)-c2(t)。继续重复上述步骤，最终可得到n阶IMF，原始振动信号S(t)可表示为

其中，rn(t)为残余函数，表示振动信号的平均趋势。

3.2 基于样本熵的特征量提取

对于一组振动信号数据序列{si}，其样本熵的具体计算步骤如下[10]：

(1)将振动信号数据序列{si}={s(1),s(2),…,s(N)}依序构造成m维矢量，S(1)，…，S(N-m+1)，其中，

Si={s(i),s(i+1),…,s(i+m-1)}，

i=1,2,…,N-m+1。

(2)将S(i)与S(j)间(i≠j)的距离定义为两者对应元素中差值最大的一个，即

d[S(i),S(j)]=max0-(m-1)|s(i+k)-s(j+k)|

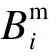
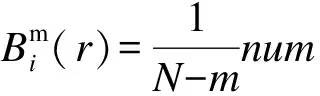
(5)将维数m加1，重复步骤(1)～(4)，得到Bm+1(r)i和Bm+1(r)。

其中，Bm(r)是由振动信号构造得到的数据序列中两个数据序列在相似容限r下匹配m个点的概率，Bm+1(r)是振动信号构造得到的数据序列中两个数据序列在相似容限r下匹配m+1个点的概率。

(6)理论上，此振动信号数据序列的样本熵为

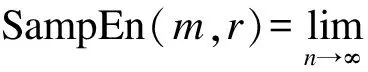
但是，在实际计算过程中，N不可能取得无穷大，而为有限值，因此将样本熵记为

SampEn(m,r)=lim{-ln[Bm+1(r)/Bm(r)]}

通常，m=1或2，r取值为原始振动信号数据序列方差的0.1～0.25倍。

3.3 配电开关机械状态FCM聚类诊断

首先，将振动信号的各阶IMF样本熵值构成的矩阵设为X={xi}，作为FCM的输入。预先给定分类数c和加权指数m，初始化隶属度矩阵

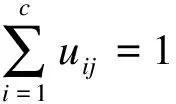
接着，计算聚类中心

构造新的隶属度矩阵

Uc×n={uij}

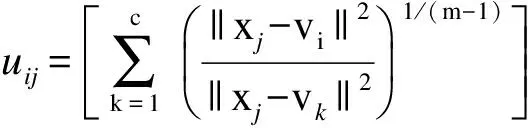
uij满足以下3个条件：

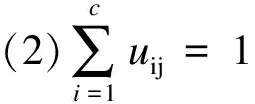
FCM的目标函数为

其中，1

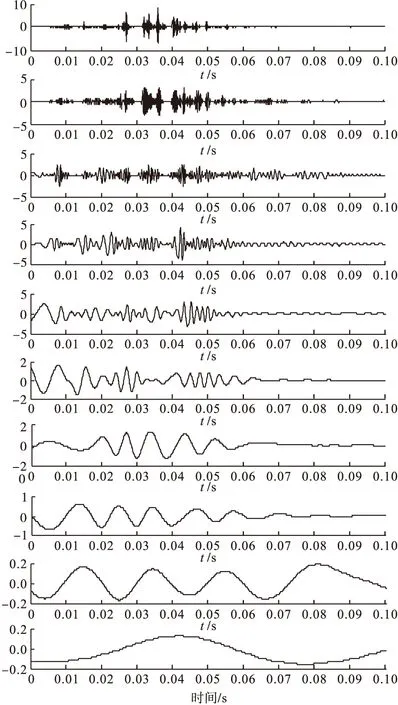
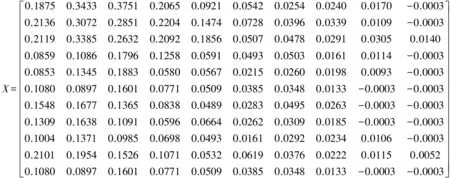
4 实测数据分析

在配电开关厂振动磨合实验室内，以中压SF6绝缘环网负荷开关为研究对象，通过人工模拟故障的方式进行了大量的实验。在实验中，需注意压电式传感器的安装位置的选取问题。配电开关的分、合闸振动信号是由沿一定路径传播的多个衰减振动波叠加而成的，振动波在机构内部的传播过程、传播途径、衰减、折反射情况复杂，将压电式传感器安装在不同位置上采集到的振动信号波形会有很大差别。在采集振动信号时，应尽可能将传感器安装在靠近振源的位置上，以减小振动传播路径对采集到的振动信号的影响。本次实验中，将压电式加速度传感器安装在开关操动机构主轴附近。以80kHz的采样频率采集了正常状态、机械结构卡涩状态和底座螺丝松动等状态下的开关分、合闸振动信号。考虑到实验中的环境等随机因素可能对采集到的振动信号产生影响，故对上述三类机械状态下的振动信号分别进行3～5次的采集，比较同类状态下的波形信号，若波形形状相似、呈现出相同的特征信息，则可作为进一步分析的有效信号。

图3 压电式加速度传感器安装位置示意图

对上述3类机械状态下的配电开关合闸振动信号进行分析，对各类机械状态各取3组作为样本数据，任意取2组作为待检测状态数据。对这11组振动信号波形数据进行编号，编号1、2、3为正常状态，编号4、5、6为机械结构卡涩状态，编号7、8、9为底座螺丝松动状态，编号10、11为待检测状态。观察初始信号波形如图5所示，从信号幅值大于设定阈值3.3V开始，往前取0.0075s，往后取0.0925s，共计0.1s的振动信号作为待分析有效信号。信号1、4、7的原始波形如图4所示。

对这11组信号进行EMD，得到各组信号频率从高到低排列的10阶IMF，图5列出了信号1的10阶IMF，由图可以看出，配电开关机械状态信息主要体现在高频段内。

取维数m=2，计算EMD后11组信号各阶IMF的样本熵值，得到一组样本熵矩阵X，其中各行从上至下依次对应编号1-11所定义的机械状态，各列从左至右依次对应该编号机械状态下合闸振动信号各阶IMF的样本熵值。

以X作为FCM聚类的输入，设置FCM聚类数目c为3，加权指数m为2，迭代终止因子为ε=10-5，最大迭代数为100。聚类结果显示编号1、2、3振动信号为同类信号，编号4、5、6、10振动信号为同类信号，7、8、9、11振动信号为同类信号，与真实情况相符，实验结果验证了以振动信号各阶IMF样本熵值作为配电开关机械状态诊断特征量、利用FCM聚类对配电开关机械状态进行诊断的有效性与可行性。

图4 信号1、4、7的原始波形图

图5 信号1的10阶IMF分量图

5 结语

本文建立的基于振动信号分析的配电开关机械状态诊断系统，通过合理的振动信号采集装置软硬件设计和振动信号分析方法选择，实现了对配电开关机械状态的准确诊断。

(1) 振动信号采集装置能够快速地采集、存储配电开关分、合闸振动信号，为振动信号的分析与故障类型的诊断奠定数据基础。

(2) 根据配电开关振动信号的特点，选取EMD对振动信号进行自适应的时频分解，很好地表征出信号的局部时频特征；计算分解得到的振动信号各阶IMF的样本熵值，作为机械诊断的量化依据，算法的精度和速度良好。

(3) 以振动信号各阶IMF的样本熵值构成的矩阵作为FCM的输入进行聚类，实现对配电开关机械状态的准确诊断。

[1] 孙建伟,陈垒,王玉梅,等.基于LabVIEW的断路器振动信号监测系统[J].供用电,2007,24(3):48-50.

[2] 孟永鹏,钟波,贾申利.振动分析在电力设备状态检测中的应用和发展[J].高压电器,2005,41(2):461-465.

[3] 杨忠仁,饶程，邹建,等.基于LabVIEW数据采集系统[J].重庆大学学报,2004,27(2):33-35.

[4] 陈伟根,邓帮飞,杨彬.基于振动信号经验模态分解及能量熵的高压断路器故障识别[J].高压电器,2009,45(2):90-96.

[5] 朱跃光,马宏忠,陈楷,等.基于振动信号的电力变压器故障诊断系统的开发[J].电工电能新技术,2013,32(3):116-120.

[6] 来凌红,吴虎胜,吕建新,等.基于EMD和样本熵的滚动轴承故障SVM识别[J].煤矿机械,2011,32(1):249-252.

[7] 张敏,于剑.基于划分的模糊聚类算法[J].软件学报,2004,15(6):858-868.

[8] 胡劲松,杨世锡,吴昭同,等.基于EMD和HT的旋转机械振动信号时频分析[J].振动、测试与诊断,2004,24(2):106-110.

[9] HUANG NE,STEVEN R L.The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis [C]//Proc.R.Soc.Lond.A,1998:903-996.

[10] Richman Joshua S,J.Randall Moorman.Physiological time series analysis using approximate entropy and sample entropy.Am.J.Physiol.Heart Physiol,2000,278:2039-2049.

[11] 李柏年,吴礼斌.MATLAB数据分析方法[M].北京:机械工业出版社,2012:151-152.

Mechanical States Diagnosis System the Panel Switch Based on the Analysis of Vibration Signal

HUANGRong1,CHENYong-wang2,CHENLi-chun2,GUOMou-fa1

(1.College of Electrical Engineering and Automation,Fuzhou University,Fuzhou 350108,China;2.Jinjiang Power Supply Co.Ltd.,of State Grid,Qunzhou 362200,China)

The vibration signal of the pand switch contains a wealth of information about the switch mechanical states. The vibration signal features can be extracted by reasonable and effective way,which can be used in the distribution switch mechanical diagnosis. According to data collected functional requirements,we designed the vibration signal acquisition device based on LabVIEW. Use the empirical mode decomposition(empirical mide decomposition,EMD) to analyze the vibration signal,extract the sample from entropy intrinsic mode components(intrinsic mode function,IMF) as a feature,and make mechanical condition diagnosis through the fuzzy C-means clustering(fuzzy C-means,FCM). Through experiments,we collected and analyzed the distribution switch vibration under the normal state and fault state,in order to verify the accuracy and effectiveness of vibration signal analysis based on the mechanical states of distribution switchgear diagnosis system.

panel switch;mechanical states;vibration signal;EMD;sample entropy;FCM.

1004-289X(2015)02-0021-06

TM56

B

2014-03-19

黄蓉(1991-)，女，硕士研究生，研究方向为配电网及其自动化技术； 陈永往(1972-)，男，学士，工程师，主要从事电网生产技术及管理工作； 陈立纯(1978-)，男，硕士，工程师，主要从事配电运行及管理工作； 郭谋发(1973-)，男，副教授，研究方向为电力系统自动化。