桥机跨中满载起吊货物时的瞬态动力学分析

郭皓，高崇仁，殷玉枫

(太原科技大学机械工程学院，太原 030024)

桥机跨中满载起吊货物时的瞬态动力学分析

郭皓，高崇仁，殷玉枫

(太原科技大学机械工程学院，太原 030024)

运用振动力学知识建立桥式起重机桥架结构起吊货物这一动态过程的动力学模型，比较准确的计算出了钢丝绳从张紧开始受力阶段到货物离地瞬间所需要的时间，并绘制出桥架结构起吊货物时的载荷曲线。最后应用有限元分析软件ANSYS Workbench进行瞬态动力学分析，得到结构的位移响应曲线，并计算出了桥架结构的起升动载系数，为现有起重机的设计方法提供了一种参考。

桥架结构;动力学模型;载荷曲线;位移响应曲线

桥式起重机在其起吊货物的过程中，由于货物的突然起升、变速升降和空中卸载等情形，都会产生惯性力的作用，由于惯性力的作用对起升机构及主要的承载构件都会产生一些附加载荷，从而造成结构的振动。因为这样的冲击载荷所产生的动力响应对桥架结构的破坏力非常大，所以在桥式起重机设计当中，其应作为主要的考虑因素之一。实践表明，货物在离地起升时产生的动力效应比下降制动时更大，因此本文主要针对货物离地起升这一工况，研究该工况下桥架结构的动力响应情况，通过ANSYS Workbench对桥架结构进行瞬态动力学分析。

1 货物离地瞬间动力学模型建立

货物离开地面起升的过程主要分三个阶段:一是起升机构的钢丝绳由松弛到张紧，但未受力;二是第一阶段中的未受力的钢丝绳逐渐受力并不断增大到与货物的重量相同，此时桥架结构和钢丝绳发生不同程度的变形，但货物仍未离开地面;第三阶段是货物离开地面的瞬间，也就是与桥架结构同时发生振动的瞬间。

在以上三个阶段当中对结构产生的动力效应最大的是第三阶段，就此建立结构、钢丝绳绕组及起吊货物的动力学模型，该模型是一个二自由度质量-刚度振动系统，模型简化如图1所示:

m1——换算以后的桥架结构的质量，包含小车质量在内，(换算质量为跨中桥架质量的一半和小车质量之和);

k1——桥架结构换算后的刚度;

m2——起升的总质量，包含吊具;

k2——起升钢丝绳绕组的刚度。

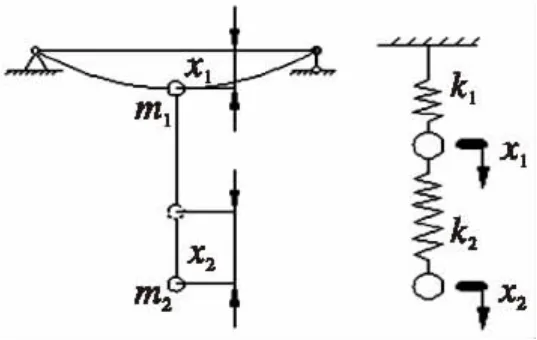
图1 货物离地面瞬间结构及钢丝绳绕组的动力学模型Fig.1 The structure at the instant of goods leaving off ground and the dynamical model of wire rope winding

由货物离开地面起升过程的三个阶段可知:在钢丝绳处于预紧阶段时，总的起升质量m2还没有离开地面，此时引发m2产生振动的激励是小车架上钢丝绳的弹性张力，即:

(1) 不同损伤岩样表现出的峰后蠕变特性具有明显的差别。随着损伤的加大，蠕变变形速率增大，蠕变失稳时间缩短，越容易发生失稳破坏。

在钢丝绳的预紧状态将要结束的瞬间，货物与地面之间处于似离非离的临界状态，此时的钢丝绳的弹性张力的值与起升总质量m2的重力相等。由牛顿第二定律可以得出预张紧过程当中m1的运动微分方程为:

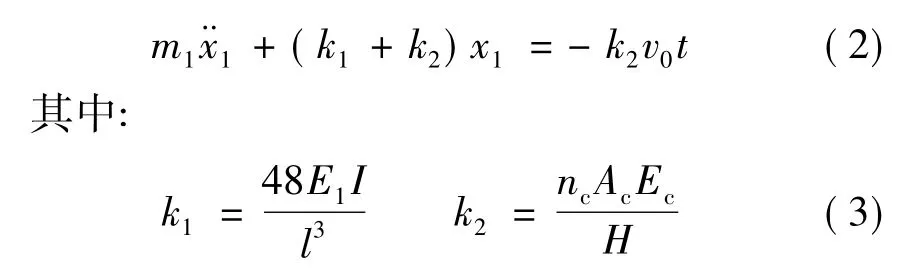
l——桥架的跨度;

E1——桥式起重机结构的弹性模量;

I——主梁截面惯性矩;

nc——滑轮绕组的分支数;

Ac——单根钢丝绳截面积;

Ec——钢丝绳纵向的弹性模量;

H——桥式起重机额定起升高度。

当初始时刻也就是零时刻时，求解上述方程(2)得:

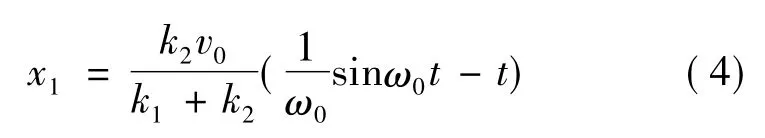
其中ω0为此阶段的固有频率:

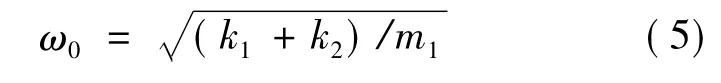
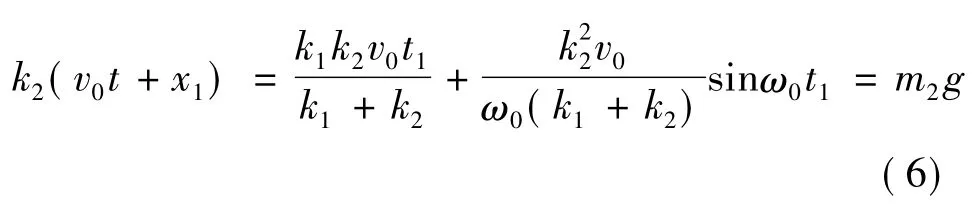
2 起升过程载荷曲线

将式(4)(5)代入下式得货物离开地面瞬间方程式:

本文主要针对的是货物起升过程中的第二和第三阶段的研究，通过计算机虚拟技术模拟出桥架结构在吊重这一激励作用下的动态响应情况。随时间变化的加载过程如图2所示:

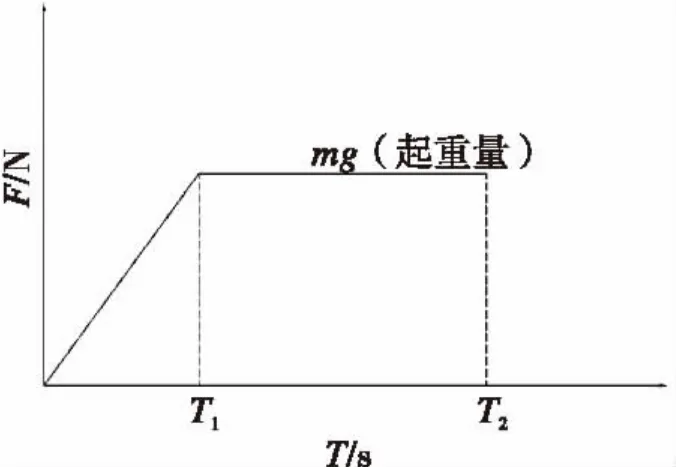
图2 起升冲击载荷加载过程Fig.2 Hoisting impact load curve

由图2可以看出0-T1阶段为钢丝绳的预紧阶段，此时载荷的大小由0开始呈线性增长，T1时刻达到最大值。T1-T2阶段为货物的起升阶段，该过程中，起吊的载荷大小始终保持不变。由于起升高度和起升速度都是已知和确定的，那么图中T1-T2阶段的历时就能够得出，则0-T1阶段时间的确定对货物离开地面瞬间的动力响应分析起到非常重要的作用。

由现有起重机参考资料，选取的桥式起重机参数如下:起升速度为v0=2 m/min，起升高度为H= 17.5 m，桥机跨度为l=28.5 m，主梁的质量为m主= 92 982 kg，起升总质量m2=512 000 kg，m1=m小车+

将已知值代入公式(3)(5)计算得:

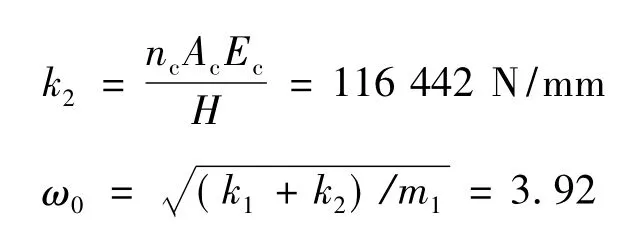
将各参数代入货物离开地面瞬间的方程式(6)，通过计算机编程计算得t1=2.11 s.

3 各类响应曲线的获取

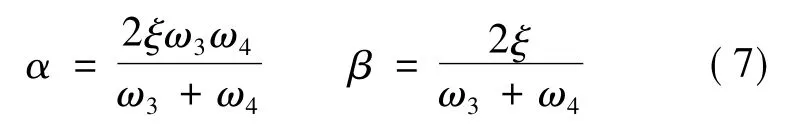
其中:ξ——阻尼比;

ξ的取值通常是在0.008～0.05之间，采用焊接结构的，ξ在0.008～0.01范围内选取，铆接结构在0.015～0.05，由于箱型结构的通用桥式起重机一般情况下都是由板材焊接组合而成的，也就是所谓的焊接结构。所以本文中选取ξ=0.009.

ω3——起升机构起升时的固有频率;

ω4——起升机构制动时的固有频率;

ω3、ω4的取值可由模态分析中由起升机构起升、制动时引起的振动频率f3=11.745 Hz，f4= 12.038 Hz得出，由:

计算得出ω3=75.583，ω4=75.253，将ξ、ω3、ω4的值代式(7)可得:

在用ANSYS Workbench软件进行瞬态动力分析时，阻尼参数α、β的取值通过阻尼比ξ来计算。其计算公式如下:

通过运用ANSYS Workbench中的瞬态动力学分析模块进行分析求解，可以得出桥架垂直方向上随时间变化的最大位移响应曲线、最大及最小速度、加速度响应曲线，分别如图3-5所示。

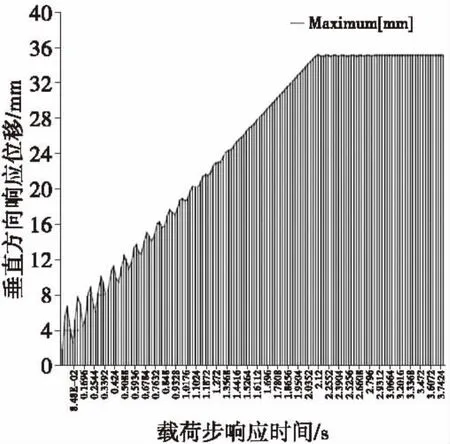
图3 主梁最大位移响应曲线Fig.3 The displacement response curve of girder

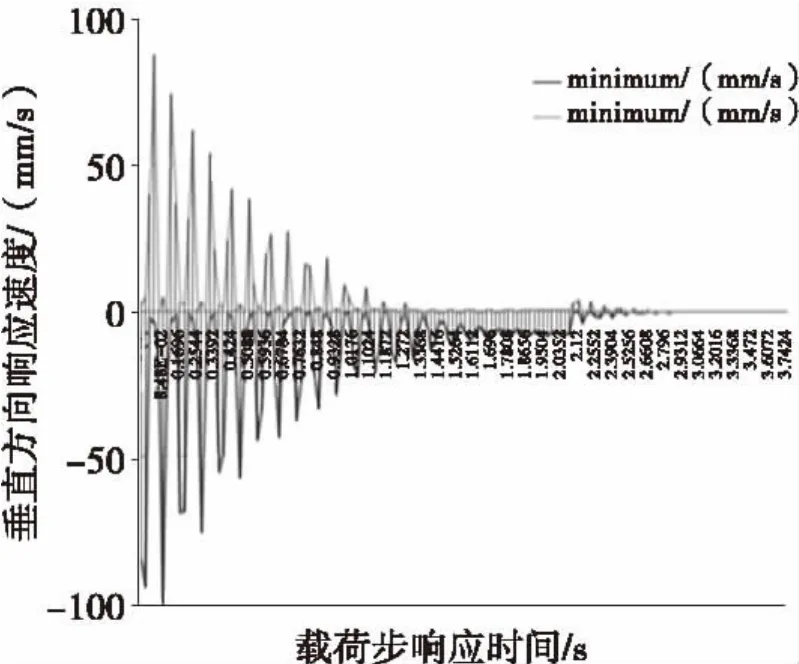
图4 主梁速度响应曲线Fig.4 The velocity response curve of girder

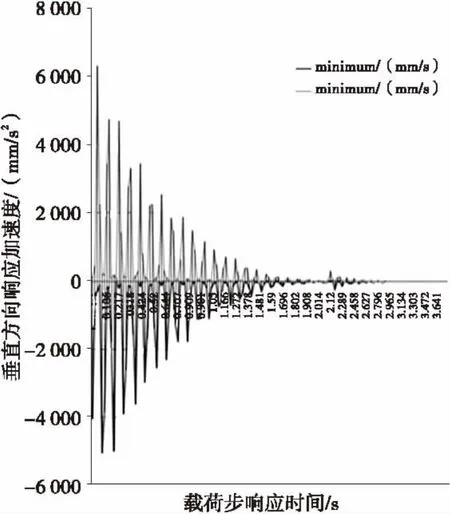
图5 主梁加速度响应曲线Fig.5 The acceleration response curve of girder

4 结果分析

通过对计算结果的分析可得出以下结论:

(1)由图3的主梁最大位移响应曲线图可得出桥架结构在随着时间变化的载荷作用下的动位移最大值为35.356 mm，即δd=35.356 mm.

(2)因为考虑阻尼的作用，桥架结构在变载荷的作用下振幅是递减的，即由瞬态响应变成稳态响应，直至最后衰减到一个平衡位置，由图3～5可得出衰减时间大概为3 s左右，这个结果与起重机设计规范中的要求是相符的。

(3)由图3可以观察出位移随着时间变化的响应曲线与随时间变化的载荷曲线是基本相符的，也就是说桥架结构的位移变化是与载荷的加载情形大体呈线性比例的关系，这与实际起吊货物中的情况相符，以此对上述计算方法的正确性进行了验证。

(4)桥式起重机的结构设计当中，通常要将额定起升载荷放大一定量的倍数来设计桥架结构，也就是用额定载荷乘以大于1的动载系数φ2来计算和确定桥架的结构形式。一般的情况下，φ2的取值由桥架结构等效简化成的自由振动系统的最大位移δd与货物离地瞬间的额定起升载荷对结构吊重部位产生的最大静位移δ0(跨中最大的静位移)之比进行估算得到，即:

在前期的研究中，通过已对桥架的静力学分析可得δ0=33.943 mm，代入式(9)得出:

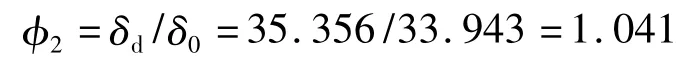
而经过传统计算得出的φ2=1.167，误差率达到10.7%.

5 结束语

在起重机设计过程中，动载系数的选取至关重要，取值偏大的话，设计出的桥架结构笨重，取值偏小了，结构安全性能则会降低。该动载系数的计算为现有起重机的设计方法提供了一种参考思路。

［1］杨海明，秦义校，张超，等.铸造起重机桥架结构分析与局部改进［J］.太原科技大学学报，2012，9(1):30-35.

［2］浦广益.ANSYS Workbench 12基础教程与实例详解［M］.北京:中国水利水电出版社，2010.

［3］孙彦锋.基于ANSYS的龙门起重机结构系统谐响应分析［J］.现代机械，2009，20(8):32-33.

［4］Richard Julien，Koboevic Sanda Tremblay，Robert.Seismic design and response of crane-supporting and heavy industrial steel structures［J］.Engineering Journal，2011，48(3):205-224.

［5］黄捷，崔宏飞.通用桥式起重机结构动响应研究［J］.科学技术与程，2009，18(2):6326-6329.

［6］李欣灿，周诗洋.基于ANSYS的桥式起重机动态分析［J］.湖北工业大学学报，2012，27(4):18-21.

［7］孙民，王志远，付为刚.桥式起重机起吊过程的动力学分析［J］.机械，2010，2(5):1-12.

Analysis of Transient Dynamics for Overhead Crane Lifting Full Load

GUO Hao，GAO Chong-ren，YIN Yu-feng
(College of Mechanical Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

The time of wire rope from tension stress stage to the goods just leaving off the ground can be accurately calculated by building the dynamic model of bridge structure lifting goods with vibration mechanics knowledge，the load curve of bridge structure lifting goods can also be drawn out.Finally，the structure displacement response curve can be got by using the finite element analysis software ANSYS Workbench for transient dynamics analysis.At the same time，the lifting dynamic load coefficient of bridge structure can be calculated，which provides a reference for crane design.

bridge structure，dynamic model，load curve，displacement response curve

TH215

A

10.3969/j.issn.1673-2057.2015.02.012

1673-2057(2015)02-0143-04

2014-12-11

郭皓(1988-)，女，硕士研究生，主要研究方向为机械工程。