基于角度调谐的光子晶体滤波特性研究

张 杨,温建华,杨毅彪,b,费宏明,陈智辉,b

(太原理工大学 a.物理与光电工程学院,b.新型传感器与智能控制教育部重点实验室,太原 030024)

基于角度调谐的光子晶体滤波特性研究

张 杨a,温建华a,杨毅彪a,b,费宏明a,陈智辉a,b

(太原理工大学 a.物理与光电工程学院,b.新型传感器与智能控制教育部重点实验室,太原 030024)

提出一种含CaF2缺陷层的一维光子晶体结构,可用于光通信波段的可调谐滤波。通过传输矩阵理论对滤波器透射特性进行分析,结果表明:随着周期数目的增加,光子晶体禁带截止度增强,缺陷模半高宽逐渐变窄，同时缺陷层厚度增加使缺陷峰的位置均匀红移;正入射时,所设计滤波器结构的光子禁带范围是1 170～2 150 nm;当入射角增大至掠入射过程中,TE模式全角度光子禁带为1 170～2 035 nm,TM模式全角度光子禁带为1 170～1 640 nm,表明TM模式禁带对入射角度的变化较敏感。研究发现,选取较大的入射角度或增加光子晶体周期数可以使TM,TE模式透射峰完全分离，通过角度调谐方式可实现光通信S波段两种模式的滤波。该光子晶体滤波器具有高透射率,窄半高宽,宽调谐范围的滤波特性,可有效提高传统滤波器的滤波性能。

一维光子晶体;传输矩阵法;可调滤波器;通信波段;光子禁带

可调谐光滤波器是一种波长选择器件,在光纤通信和光纤传感领域中具有广泛的应用,是波分复用(WDM)光传输系统,光纤布拉格光栅(FBG)传感系统和光纤可调谐激光器中的关键组件[1]。介质膜[2]、F-P腔[3]、微环谐振腔[4]、光纤光栅[5]等都是各具特色有发展潜力的可调谐滤波技术,但这些技术进入实际应用阶段前也还需要解决各自的一些问题。例如,各类F-P腔滤波器精细度和自由光谱区难以同时满足OPM对选频和调谐范围的要求。介质膜TFF滤波器需要利用多个F-P腔的级联提高器件隔离度,会影响输出光功率的稳定性。光纤光栅型滤波器应用于多通道分波时,采用级联结构需大量的FBG;采用加环形器反射结构会带来额外的损耗。微环谐振腔滤波器的研究在向多环级联发展,需解决环间谐振调谐与耦合系数精确控制问题。光子晶体[6-7]具有光损耗低、尺寸小、易于集成等优点,由于近些年制备技术趋于成熟而被人们大量的研究。光子晶体是1987年被提出的不同介质材料在一维、二维、三维空间呈周期性排列的人造晶体[8-9],具有光子带隙和光子局域两大特性。在光子晶体中引入其它介质[10-11]或改变其中介质的等效光学厚度[12],光子晶体的周期性被破坏,使带隙中出现缺陷模,利用这种含缺陷的一维光子晶体可以达到光滤波的目的。基于光子晶体实现可调谐滤波主要是利用磁场[13-14]、电场[15-16]、热量[17]等外界条件,改变材料的折射率和介质层的厚度实现可调谐滤波,但是这些方法都存在着不足:对磁场、电压和温度等外界的条件要求很高,利用热光效应具有调谐范围窄的缺点,电光效应具有响应速度慢等局限,且这类调谐方式一般都需要借助校准层或调整层用以给目标层施加外场实现可调。

笔者在光子晶体中引入CaF2作为缺陷层构成滤波器结构(SiO2/Si)M/CaF2/(SiO2/Si)N,利用改变入射角实现调谐滤波,避免了外界条件如电场和校准层等的介入及其响应时间。采用传输矩阵法对该滤波器结构的能带特性进行了研究,讨论了不同缺陷层厚度、缺陷两侧周期数目及各入射角度下的滤波特性,分析了同一入射角度TE模、TM模的透射谱,并针对光通信S波段的光传输滤波做了具体研究。

1 结构模型和理论方法

图1是一维光子晶体滤波器结构模型(SiO2/Si)M/CaF2/(SiO2/Si)N,其中蓝色代表低折射率材料SiO2,折射率为1.444；红色代表高折射率材料Si,折射率为3.478；黑色部分为CaF2缺陷层,折射率为1.426,θ为光入射角度。为了使光子晶体的禁带范围落在近红外波段,晶格常数取值为372 nm,各介质层厚度为dSiO2=263 nm,dSi=109 nm.所选的材料Si,SiO2，CaF2是常用的红外光学材料,在近红外波段具有良好的透过率,性质稳定受外界环境影响较低,材料采集较廉价,可降低实验成本。

本文采用传输矩阵法计算所设计一维光子晶体滤波器结构TE和TM两种模式的透射谱。电磁波在光子晶体中传播时,反射光与透射光是由电磁波逐层传播后在反射区域和透射区域相干叠加形成的。光入射时的角度影响透射光的偏振特性,所以应分别讨论TE模式和TM模式下的传输矩证理论。电磁波在介质交界层产生反射和折射,且电磁场强度的切向分量在交界面处连续,TE模式下,一维光子晶体中任意第j层的传输矩阵的表达式为:

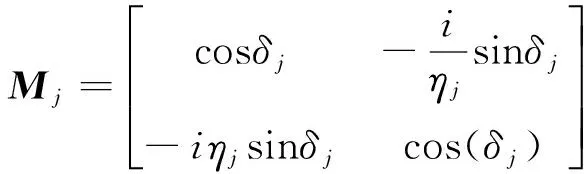
(1)

式中：δj为电磁波在第j层上下两个界面之间传播时的相位变化；ηj为第j层膜的光学导纳。所设计的光子晶体结构有2(M+N)+1层介质,有2(M+N)+2个界面,所以光波从第1个界面传播到第2(M+N)+2个界面时的传输矩阵公式为:

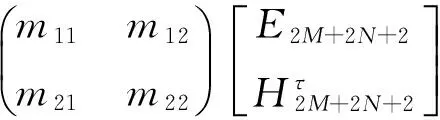
(2)

把一维光子晶体的结构参数代入得到透射系数:

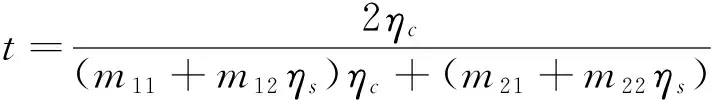
(3)

式中，ηc与ηs分别是入射区和透射区的光学导纳,则透射率为:

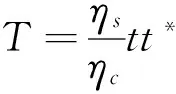
(4)

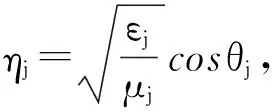
2 数值模拟结果与讨论

2.1 一维光子晶体的透射谱

首先计算结构为 (SiO2/Si)N(SiO2/Si)N的一维光子晶体透射谱,其中结构参数nSiO2=1.444,nSi=3.478,dSiO2=263 nm,dSi=109 nm,θ=0°,周期数N分别取4，5，6时的结果，如图2所示。

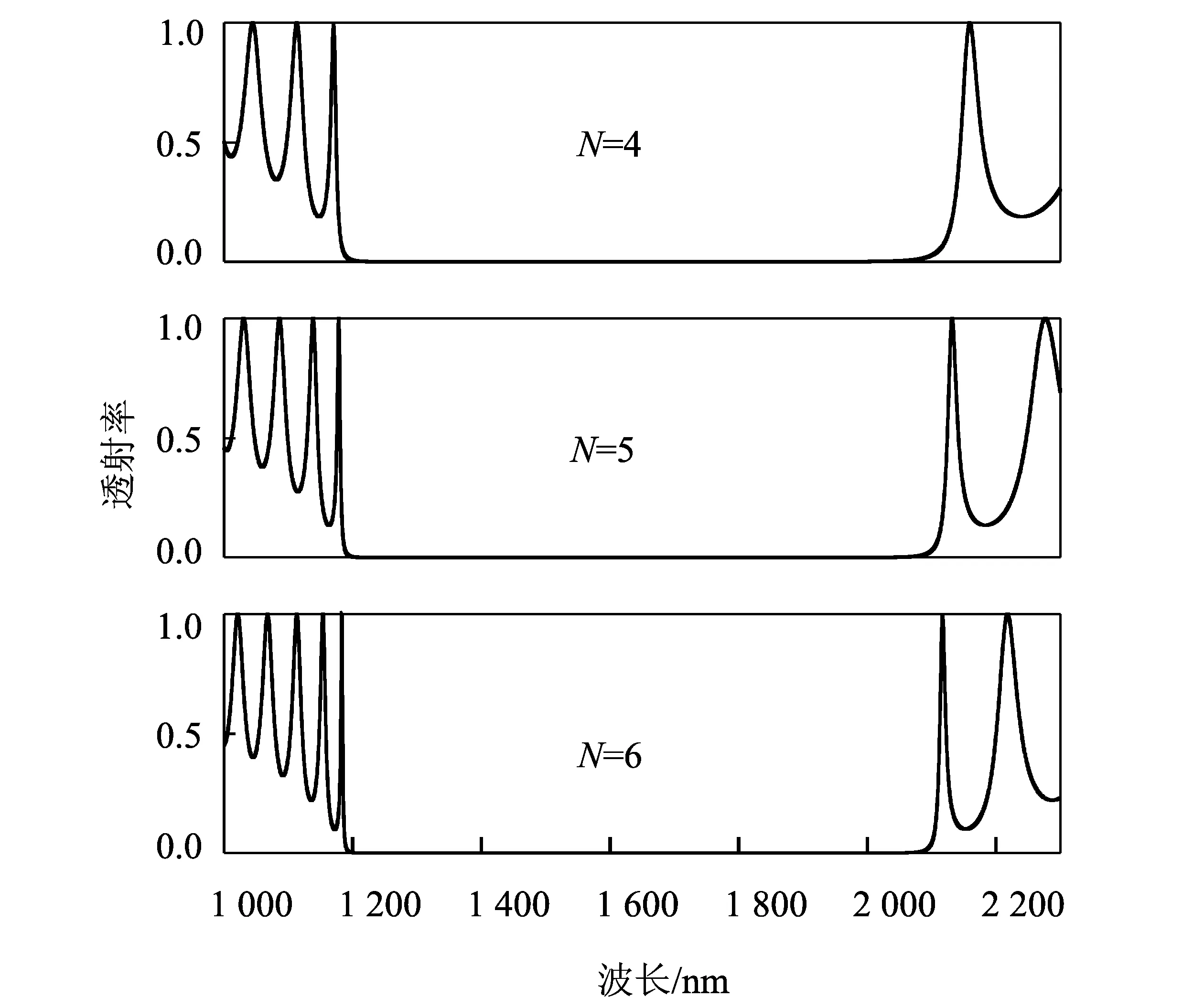
图2 周期数N为4,5,6时,一维光子晶体的透射谱

从图2中可以看出,周期数N分别取4，5，6 时,光子晶体的禁带范围基本没有发生改变,禁带都在1 170～2 150 nm之间,范围完全覆盖了ITU-T规定的光通信S波段。同时随着光子晶体周期数的增加,光子晶体禁带边缘变的越来越陡直,即截止度提高。

2.2 缺陷层厚度对透射谱的影响

在正常光子晶体中插入缺陷层破坏其周期性,使光子禁带中某频率的光受到缺陷两边周期性光子晶体的影响,被限制在缺陷中往返震荡加强后继续向前传播,原来的禁带中就出现了缺陷态。随着缺陷层厚度增加,振荡空间变大,带结构中处于高能带的离散模被推向低禁带中,光频率降低[18],缺陷态频率发生移动。在上述结构中间插入缺陷层CaF2,一维光子晶体滤波器的结构为(SiO2/Si)N/CaF2/(SiO2/Si)N,模拟CaF2层的厚度对光子晶体滤波器透射谱的影响,结果如图3所示。其中参数nSiO2=1.444,nSi=3.478,nCaF2=1.426,dSiO2=263 nm,dSi=109 nm,θ=0°,N=4.

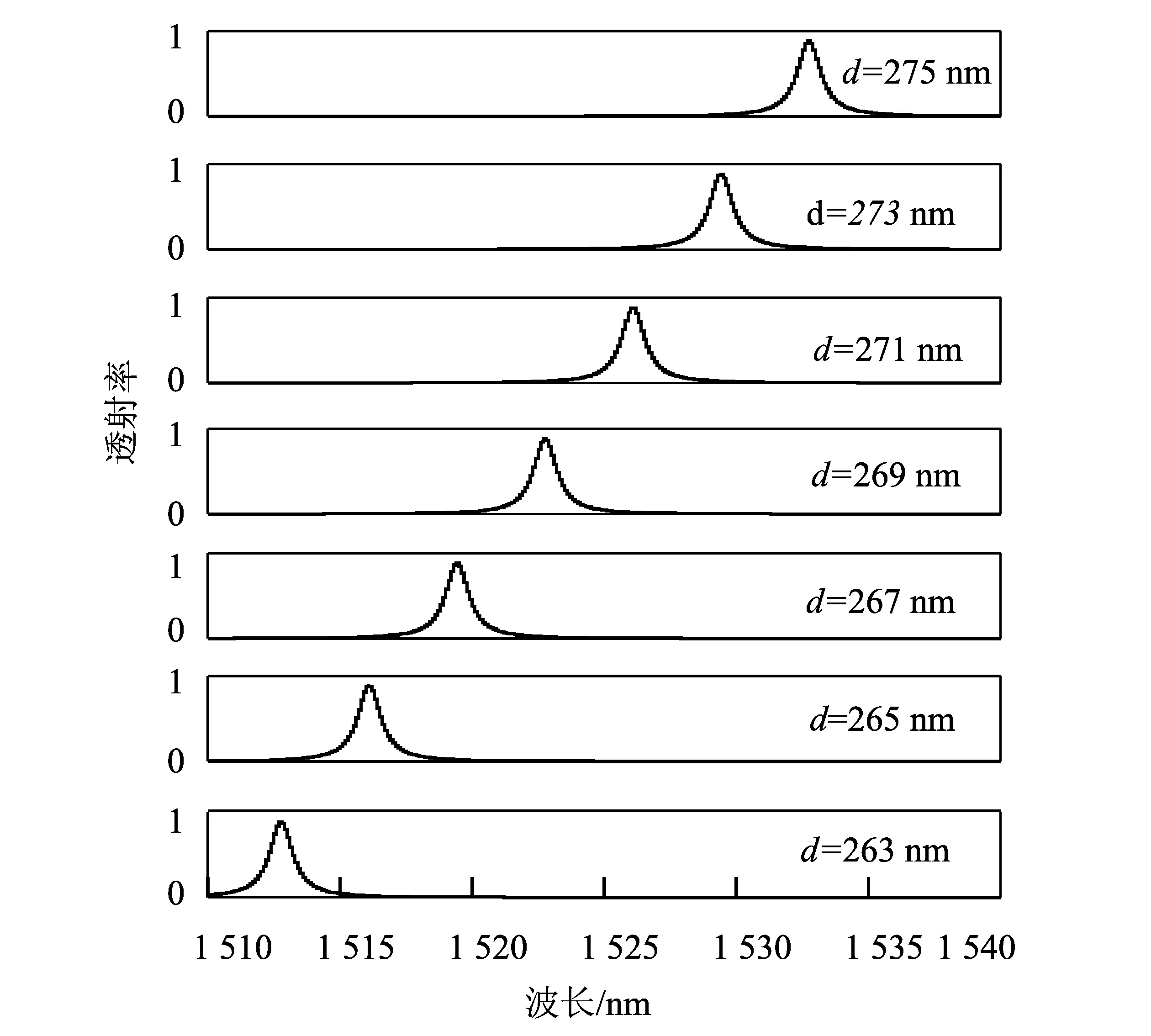
图3 周期数N=4时,随着CaF2的厚度变化滤波器的透射谱

从图3中分析可得，随着缺陷层厚度的减小,光子晶体缺陷峰的中心波长向短波方向移动,当厚度由275 nm每隔2 nm减小到263 nm时,缺陷峰中心波长的位置分别为1 532.65，1 529.35，1 526.05，1 522.75，1 519.45，1 516.15,1 512.85 nm,半高宽均为1.06 nm,缺陷层的厚度每变化2 nm,其缺陷峰对应中心波长位置移动3.3 nm.当缺陷层的厚度为267 nm时,缺陷峰的中心波长为1 519.45 nm,位于光通信S波段的右边缘。为了使缺陷峰的移动范围覆盖光通信S波段,在下文研究斜入射时取CaF2层的厚度值为267 nm.

2.3 缺陷层两侧周期数对其透射谱的影响

数值模拟一维光子晶体滤波器结构(SiO2/Si)M/CaF2/(SiO2/Si)N缺陷两侧的周期数目M,N取不同数值时对其透射特性的影响,结果如图4所示。其中固定CaF2层厚度为267 nm,SiO2和 Si的参数不变。

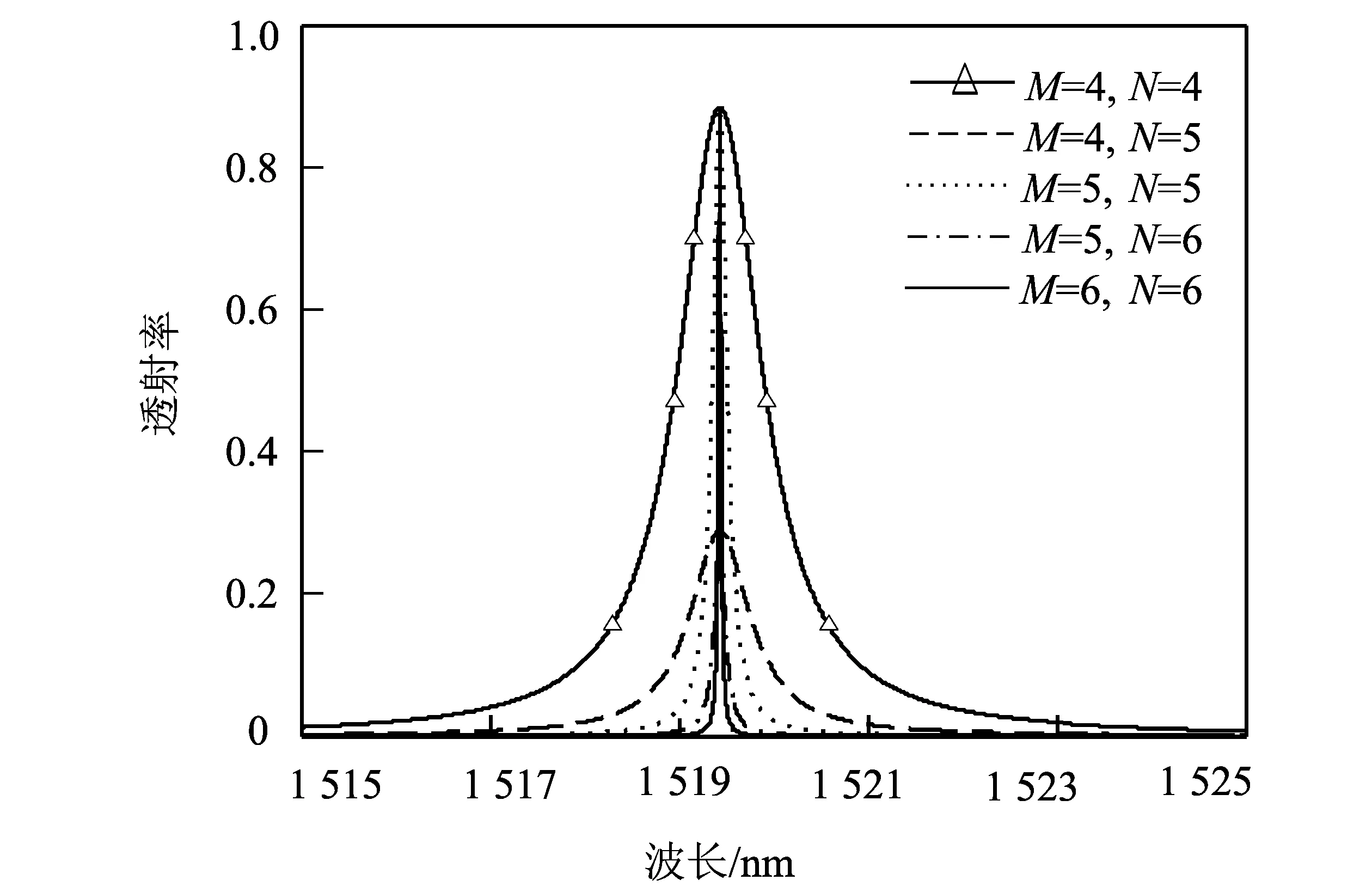
图4 M、N取不同值时,滤波器的透射谱

由图4可知,峰值均在1 519.4 nm处,缺陷层两侧周期数不影响共振缺陷峰中心波长位置。当缺陷层两侧的周期数M=N时,峰值透射率高达89%以上,但当周期数M≠N时,峰值透射率不到28.8%,远远低于缺陷两侧周期数相等时的透过率。周期数目M=N=4时,M=4,N=5时,M=N=5时,M=5,N=6时,M=N=6时,半高宽分别为1.06，0.7，0.183，0.134，0.031 nm,逐渐变窄。结果表明，缺陷层两侧周期数目相等时,一维光子晶体滤波器结构具有高的透射率;随着光子晶体周期数目的增加,半高宽在逐渐降低,当增大到一定数目时,可实现窄带滤波。基于此结果,可以实现高透过率的窄带滤波,应用于密集波分复用系统。

2.4 入射角度对透射谱的影响

随着光入射到光子晶体滤波器角度的改变,不同的光学导纳使得两种模式对应的透射谱也不尽相同,以下模拟计算各入射角度一维光子晶体滤波器结构的透射谱,图5和图6分别为TE模式和TM模式的结果。

从图5中可以看出，对于TE模式,当入射角θ从0°增加到89°,光子晶体的禁带左右边缘均发生红移,禁带左边缘移动的幅度大,光子禁带范围增大;周期数N=4，5，6时,q全角度光子禁带分别为1 170～2 120 nm，1 170～2 068 nm，1 170～2 035 nm,与正入射时光子禁带1 170～2 150 nm相比较,其全角度光子禁带分别减小了30，82，115 nm.说明随着周期数的增加,全角度光子禁带的范围减小。周期数N=4，5，6时,缺陷峰的位置均从1 519.4 nm变化到1 207.25 nm (θ=75°),当入射角θ=89°时,完全禁带内已经没有缺陷模。图5中显示,TE模式下,对于每个周期数下的滤波器结构,随着入射角度的增大透射率降低,其原因是角度的增大使光子晶体每个介质层的有效厚度d增加,从而透射率值降低。

从图6中可以看出，对于TM模式来说,当θ从0°增加到89°时,光子禁带的左右边缘发生红移,禁带右边缘移动幅度远大于禁带左边缘的移动,光子禁带的范围明显减小,禁带范围的变化速度比TE模快,变化趋势与TE模相反;周期数为4，5，6时,其全角度光子禁带分别为1 170～1 682 nm，1 170～1 650 nm，1 170～1 630 nm,与正入射时光子禁带1170～2150nm相比较,其全角度光子禁带分别减小了468，500，520 nm,随着周期数目的增加,全角度光子禁带在减小,这与TE模式的一样。当θ从0°增加到89°,周期数N=4，N=5，N=6时,缺陷峰的位置从1 520 nm分别移动到1 212,1 218.7,1 221 nm,可见同一角度下周期数对TM模透射峰值有着影响。图6b显示,当入射角度从0°增加到60°时,TM模式缺陷态的透射率也随之增加,且透射率在80%以上,当入射角度大于60°时,其透射率急剧降低,这与TE模式的透射率也有很大区别。

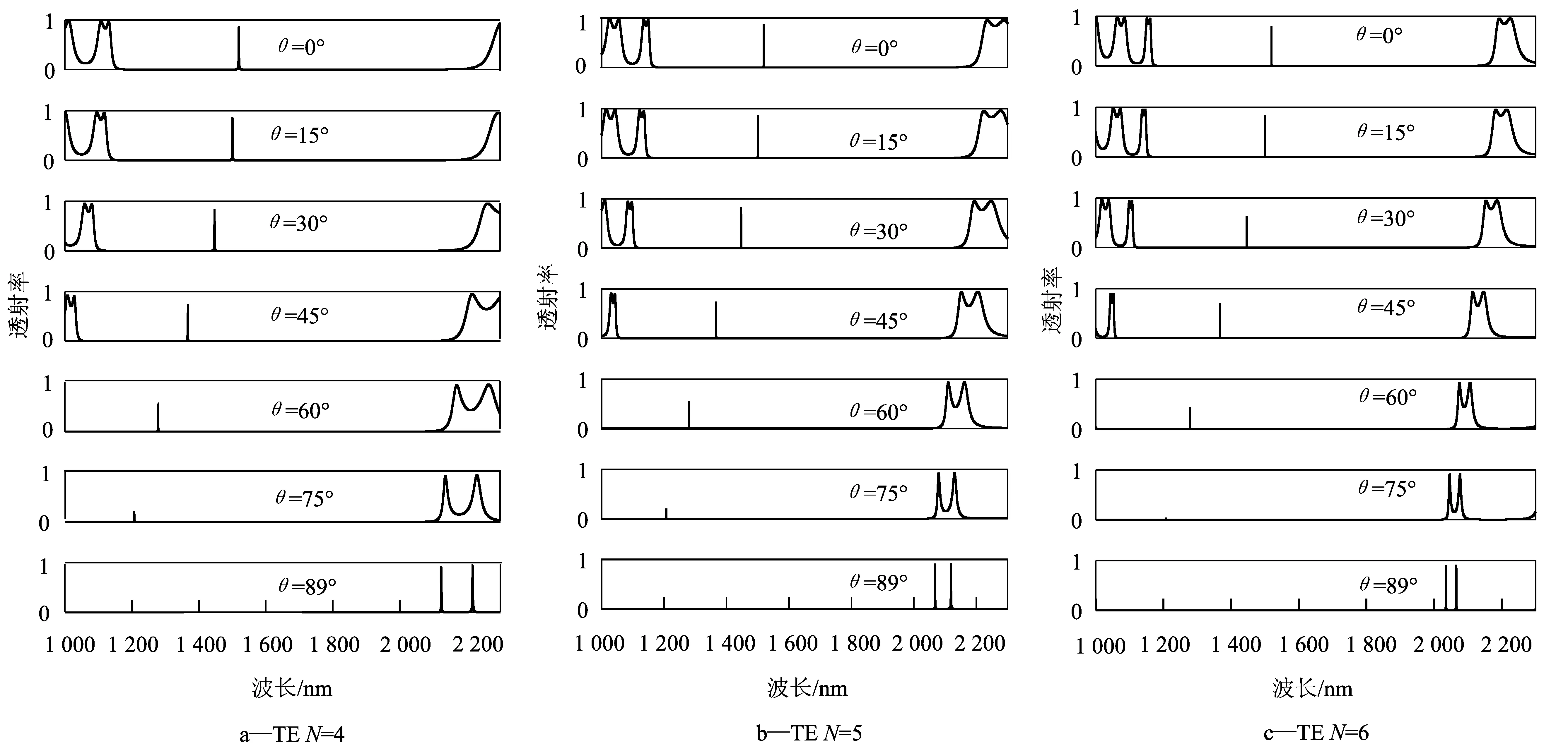
图5 不同周期下,入射角θ为0°，15°，30°，45°，60°，75°，89°时,TE模式的透射谱

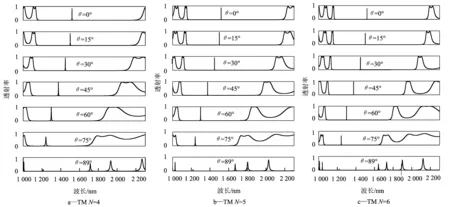
图6 不同周期下,入射角θ为0°，15°，30°，45°，60°，75°，89°时,TM模式的透射谱

对于TE模和TM模式的透射谱,随着入射角度的增大,峰值中心波长的位置向短波方向移动;TE模式的禁带随入射角度的变化不明显,TM模式禁带随入射角有着明显的改变,表明TE模式的禁带对角度的变化不敏感,而TM模式的禁带对角度变化敏感,这是因为TM和TE模带隙宽度分别由材料的磁导率和介电常数决定,这里选用的构成材料是介电材料,磁导率值取1,显然比介电常数小,所以光以一定角度射入晶体时TE模的禁带宽度要大些。

2.5 光通信S波段的滤波

为了通过调节光入射到光子晶体的角度达到调谐范围覆盖光通信S波段的目的,数值模拟了入射角度θ与缺陷峰波长的关系,其结果如图7所示。

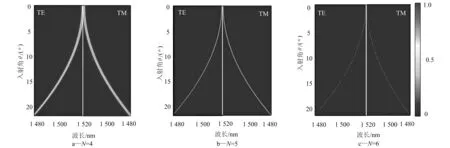
图7 透射峰从1 520 nm变化到1 480 nm时,入射角度的变化

从图7可知，对于TE模式,当入射角度θ从0°变化到21.7°时,缺陷峰的中心波长位置由1 519.4 nm移动到1 480 nm,实现了整个光通信S波段的可调滤波;对于TM模式,当入射角度θ从0°变化到22°时,缺陷峰的中心波长位置由1 519.4 nm移到1 480 nm,也实现了整个光通信S波段的可调滤波;随着光子晶体周期数目的增加,缺陷峰的半高宽和透射率均逐渐降低,主要原因是,光子晶体周期数目的增加使得缺陷层对光子晶体的周期性结构的破坏性降低,即光子局域的能力下降。若要实现窄带滤波,需要选择高周期数的光子晶体滤波器结构,但由于其会导致透射率的降低,因此应该综合考虑这两个方面的因素。

2.6 入射角度对TE、TM透射谱的影响

研究不同周期下,TE模式和TM模式透射峰在同一角度的偏移情况。这里分别研究了入射角度为14°和21.7°时,TE模式和TM模式的透射谱,结果如图8所示。

从图8中可以看出,在入射角为14°,N=4时,TE、TM模式缺陷峰的中心波长一样都是1 502.96 nm,没有发生偏移;在N=5时,TE模式缺陷峰的中心波长为1 502.955 nm,TM模式缺陷峰的中心波长为1 503.015 nm,偏移0.06 nm,半高宽为0.16 nm,偏移了3/8倍的半高宽;N=6时,TE模式缺陷峰的中心波长为1 502.959 nm,TM模式缺陷峰中心波长为1 503.021 nm,偏移0.062 nm,半高宽为0.028 5 nm,偏移了41/19倍的半高宽。从图8中可以看出,在入射角为21.7°,N=4时TE模式缺陷峰的中心波长为1 480.41 nm,TM模式缺陷峰中心波长为1 480.85 nm,偏移0.44 nm,半高宽为0.8 nm,偏移11/40倍半高宽;N=5时,TE模式缺陷峰的中心波长为1 480.44 nm,TM的中心波长为1 480.88 nm,偏移0.44 nm,半高宽为0.14 nm,偏移22/7倍半高宽;N=6时,TE模式缺陷峰的中心波长为1 480.45 nm,TM的中心波长为1 480.89 nm,偏移0.44 nm,半高宽为0.14 nm,偏移22/7倍半高宽。比较数据得出:同一周期数下,入射角度越大,TM和TE 模式缺陷峰中心波长位置的偏移量也越大,分离现象明显。同一入射角度下,随着周期数目的增大,TM和TE模式的缺陷峰发生分离的程度尽管很小,但周期数目的增加使得缺陷峰半高宽减少,相对于半高宽,TM和TE模缺陷峰分离也就变得越来越明显。

通过分析,可以选取较高的入射角度和较大的光子晶体周期数目去使TM、TE模式透射峰发生分离。改变缺陷层的厚度可以实现光子晶体的可调谐滤波,但是通过旋转光子晶体滤波器改变光入射角来实现可调滤波的操作更加简单,而且控制的精度也相对较高,角度调谐很好的实现了TE、TM两种模式的光传输滤波。

3 结论

基于传输矩阵法,数值模拟了一维光子晶体可调谐滤波器(SiO2/Si)M/CaF2/(SiO2/Si)N的透射特性,结果表明，随着光子晶体周期数目的增加,光子禁带截止度提高,缺陷模的半高宽明显的降低;当缺陷层两侧的周期数目M=N时,缺陷峰的透过率是周期数目M≠N时透过率的3倍以上,利用这一性质可实现高透过率的窄带滤波。入射角度从正入射变化到掠入射时,TE模式的全角度光子禁带范围与正入射时相比较最大减小了115 nm,TM模式全角度光子禁带范围最小减少了468 nm,说明TE模式的禁带对角度的变化不敏感,TM模式的禁带对角度的变化敏感;随着入射角度的增大,光子晶体缺陷峰位置发生连续移动,当入射角度从0°到21.7°(TE模)和22°(TM模)时,可以实现光通信S波段的可调谐滤波。当入射角度大于14°时,TE、TM 模式的缺陷峰会发生偏移,入射角和周期数进一步增大,TE、TM模式的缺陷峰将完全分离。利用两侧周期数目相等含缺陷层的光子晶体结构,通过旋转角度实现了偏振模式的高透射率,窄半高宽,宽调谐范围的可调谐滤波。

[1] Zhai L,Xu J,Wu Y.Design and fabrication of independent-cavity FP tunable filter[J].Opt Commun,2013,297:154-164.

[2] Herman Van De S,Johan M M.Multimirror Fabry-Perot interferometers[J].Opt Soc Am A,1985,2(8):1363-1370.

[3] Lorenzo P L Jr,Arvin I M,Faustino M B,et al.Thermo-optic coefficient of electrochemically etched porous silicon[J].Int J Electrochem Sci,2014,9(12):8079-8089.

[4] Shen A,Qiu C,Yang L Z,et al.Tunable microring based on-chip interrogator for wavelength-modulated optical sensors[J].Opt Commun,2015,340:116-120.

[5] Yun B H,Hu G H,Zhang R,et al.Tunable erbium-doped fiber ring laser based on thermo-optic polymer waveguide bragg grating[J].Opt Commun,2015,336:30-33.

[6] Shi Z J,Tang X P,Lan F,et al.Simulation of terahertz Smith-Purcell radiation from one-dimensional dielectric photonic crystal[J].J Infrared Millim Waves,2014,33(2):183-187.

[7] Shen Y,Ye D,Celanovic I,et al.Optical broadband angular selectivity[J].Science,2014,343(6178):1499-1501.

[8] Yablonovitch E.Inhibited spontaneons emission in solid-state physics and electronics[J].Phys Rev Lett,1987,58(20):2059-2062.

[9] John S.Strong localization of photons in certain disordered dielectric superlattices[J].Phys Rev Lett,1987,58(23):2486-2489.

[10] Toshiaki H.Third-order nonlinear enhancement in one-dimensional photonic crystal structures[J].Jpn J Appl Phys,2002,41(3):1349-1353.

[11] Yoshihiro A,Takashi A,Bong-Shik S,et al.High-Q photonic nanocavity in a two-dimensional photonic crystal[J].Nature,2003,425:944-966.

[12] Geesche B,Carsten H.All-frequency effective medium theory of a photonic crystal[J].Opt Express,2003,11(13):1590-1595.

[13] Wang H,Wang G J,Han Y L,et al.Tunable double-channel filter based on defect mode splitting of one-dimensional magnetic photonic crystal[J].Opt Commun,2012,285:4558-4561.

[14] Wang X Y,Zhu Z W.A novel tunable filter using magnetized plasma defect in one-dimension photonic crystal[J].Chin J lumin,2012,33(7):747-753.

[15] Wang H T,Timofeev I V,Chang K,et al.Tunable narrow-bandpass filter based on an asymmetric photonic bandgap structure with a dual-mode liquid crystal[J].Opt Express,2014,22(12):15097-15103.

[16] Lu H H,Baida F I,Ulliac G,et al.Lithium niobate photonic crystal wire cavity:Realization of a compact electro-optically tunable filter[J].Appl Phys Lett,2012,101(15):151117-1-151117-4.

[17] Exner A T,Pavlichenko I,Lotsch B V,et al.Low-cost thermo-optic imaging sensors:a detection principle based on tunable one-dimensional photonic crystals[J].ACS Appl Mater Interfaces,2013,5(5):1575-1582.

[18] Joannopoulos J D,Johnson S G,Winn J N,et al.Photonic crystals;molding the flow of light[M].Second Edition.New jersey:Princeton University Press,2008:59.

(编辑：刘笑达)

Research on Filter Characteristics of Photonic Crystal with Angle Tuning

ZHANG Yanga,WEN Jianhuaa,YANG Yibiaoa,b,FEI Hongminga,CHEN Zhihuia,b

(a.CollegeofPhysicsandOptoelectronic;b.KeyLaboratoryofAdvancedTransducersandIntelligentControlSystem,MinistryofEducation,TaiyuanUniversityofTechnology,Taiyuan030024,China)

A one-dimensional photonic crystal filter with calcium fluoride defect layer is proposed for optical communication.The transmission characteristics of the filter are analyzed on the basis of transfer matrix theory and the results suggest:with the increase of the period number of photonic crystal,the rejection rate of the band gap is increased and the FWHM of defect mode is gradually narrowing; the position of the defect peak gets red shifted uniformly with the augment of defect layer thickness.At normal incidence,the photonic band gap of the designed filter structure ranges from 1 170 nm to 2 150 nm;as the incident angle increases to grazing incidence,the omnidirectional photonic band gap ranges from 1 170 nm to 2 035 nm for TE mode and 1 170 nm to 1 640 nm for TM mode,which shows that the forbidden band of TM mode is more sensitive to the change of incident angle.It is also found that the transmission peak of TM and TE mode will become separate with a higher incident angle or larger period number of photonic crystal.The tunable filter can be realized in S band of optical communication through angle tuning.The photonic crystal filter has high transmittance,narrow FWHM,wide tuning range,and can effectively improve the traditional filter performance.

one-dimensional photonic crystal; transfer matrix method; tunable filter; communication band; photonic band gap

1007-9432(2015)06-0783-07

2015-04-15

国家自然科学基金资助项目:含单空气缺陷腔的一维光子晶体可调谐滤波特性研究(61340053,61307069，61575138)，山西省自然科学基金项目资助(2013011007-1)，北京邮电大学基金项目资助(IPOC2013A001)

张杨(1988-),女,山西运城人,硕士生,主要从事光子晶体光学器件研究,(Tel)18334706510，(E-mail)1312005400@qq.com

杨毅彪,博士,教授,主要从事光电晶体能带结构及在光电器线中的应用研究，(E-mail)yangyibiao_tyut@sohu.com

TN713，O734

A

10.16355/j.cnki.issn1007-9432tyut.2015.06.027