聚合物PA66直至断裂的全程单轴本构关系研究
于思淼, 蔡力勋, 赵国明
(1.西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室, 成都 610031; 2.西南交通大学 实验室及设备管理处, 成都 610031)
聚合物PA66直至断裂的全程单轴本构关系研究
于思淼1, 蔡力勋1, 赵国明2
(1.西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室, 成都 610031; 2.西南交通大学 实验室及设备管理处, 成都 610031)
基于有限元辅助测试方法(Finite element aided testing,FAT)对新型聚合物PA66开展了直至破坏的全程单轴本构关系的研究。另外,将VIC-3D光测所得的试样表面应变场结果与有限元模拟结果进行对比,表明通过FAT方法获得的聚合物PA66全程单轴本构关系结果准确有效。最后给出了聚合物PA66的全程单轴本构关系曲线,给出了对应Chaboche本构关系模型的参数、材料临界破断应力、破断应变、应力三轴度等,并对试样的破断机理进行了分析。
聚合物PA66; 全程单轴本构关系;有限元辅助测试方法;VIC-3D光测系统
延性材料等直圆棒试样在单轴拉伸试验中将产生颈缩,从而导致颈缩后的单轴本构关系无法直接获取。精确的直至破断的全程单轴本构关系在工程材料研究中具有重要指导作用,因而国内外研究者在该方面展开了大量的试验和理论工作。Bridgman[1]以颈缩轮廓为圆形,颈缩截面上应变均匀分布等基本假设为基础,给出了试样轴向应力的修正公式。Eduardo[2]等利用试验和数值分析的方法得出表征材料响应的弹性硬化参数,并讨论了平面应力条件下该方法的适用范围。Zhang[3]采用有限元分析预测断裂准则,验证了有限元模拟载荷-位移曲线与试验曲线的重合度。Briinig[4]完成了圆棒拉伸试样大变形和颈缩现象的数值模型,并将所得结果与理论计算结果进行对比,给出了一种获取材料全程单轴本构关系的方法,但仅通过单种材料,单根试样的试验数据与荷载-位移曲线标定材料全程本构关系的方法的精确度是值得商榷的。Dumoulin等[5]通过观察喷漆试样表面点的变化来研究矩形拉伸试样载荷-位移曲线与真应力-真应变曲线的关系,并说明了大变形时应变增长的不均匀性。Mansoo等[6]通过调整有限元中应力-应变曲线使模拟载荷-位移曲线与试验曲线一致来获取材料真应力-真应变曲线。姚迪[7]等以P-V实验曲线为判据,通过分析不同构型试样、不同种类材料和不同迭代方式下的FAT方法结果,详细地验证了FAT方法对于获取延性材料全程单轴本构关系的普适性。基于FAT方法,陈辉[8]等人通过小尺寸圆环试样单轴压缩试验,引入单轴本构关系模型进行有限元迭代计算,使模拟计算的试样变形与圆环试样压缩试验结果一致,得到了材料单轴弹塑性本构关系参数。同时,几个在等温和非等温条件下测量塑性结构大变形的公式也可用于分析相关问题[9~12]。然而,上述研究主要集中于金属材料本构关系获取,而对聚合物材料本构关系研究报道少有见到。
PA66称为聚酰胺66,俗称为尼龙双6,为五大塑料之首,广泛用于制造机械、汽车、化学与电气装置的零件,如齿轮、滚子、滑轮、辊轴等。聚合物PA66具有强度高、耐腐蚀、耐磨和自润滑等特点。一直以来针对PA66的力学性能研究集中于其添加填充剂后的性能研究,如肖华明等人[13]研究了PA66与PTEE共混后拉伸性能和弯曲性能的变化,但国内外罕见对PA66全程本构关系的研究。
随着计算机技术的发展,计算机辅助测试广泛应用于数据处理。近年来,有限元理论与方法发展成熟后,有限元辅助测试得以发展,国内外均展开了利用有限元工具对金属材料本构关系的研究。其中蔡力勋等提出了用于获取金属材料颈缩后全程本构关系的有限元辅助测试(finite-element-analysis aided testing),简称FAT方法[14],即通过不断迭代调整有限元基本物理方程(材料本构关系)以达到对材料与结构的数值模拟结果与试验结果一致,进而得到描述材料不同变形程度的等效本构关系。
本研究应用FAT方法于获取聚合物PA66直至破坏的全程等效本构关系,通过VIC-3D系统测试结果进一步验证FAT方法对获取PA66全程单轴本构关系的准确性,并对单轴漏斗试样横截面的应力三轴度演化进行分析。
应力三轴度又称三轴应力度,记为σ*其中,定义为静水压力比Mises等效应力,即σm/σe,σm代表静水压力,为主应力平均值,即
(1)
σe代表Mises等效应力,为
(2)
表征应力状态参量的应力三轴度是控制材料断裂模式的关键因素,作为影响材料断裂的因素而被引入到众多失效模型中,一般认为,应力三轴度σ*的代数值反映了应力场中三轴应力状态对材料变形的约束程度,直接影响着各点塑性变形的大小及断裂应变大小。
对特定材料,在一定范围内,应力三轴度σ*值大,应力状态偏于受拉状态,材料易于拉断;应力三轴度σ*值小,应力状态偏于受压,拉断不易发生,材料易于剪断。
1 试验装置与材料试样
试验设备为美国MTS 809 25kN电液伺服材料试验机、TestStarII控制系统、MTS790.20应用软件,采用MTS632.12c-21(标距25mm,轴向测量范围-10%~50%)应变引伸计测量室温下试样标距段颈缩前的真实应变和颈缩后的位移,通过计算机对试验过程进行闭环控制和实时数据采集。
试验材料聚合物PA66的拉伸弹性模量为3100MPa,断裂延伸率为40%。试样为漏斗区R为10mm的漏斗试样和漏斗区R为5mm的漏斗试样,试样均采用高精度数控机床加工,图1给出了两种试样的尺寸构形。

图1 试样尺寸构形 (a)PA66 R=10mm漏斗型试样;(b)PA66 R=5mm漏斗型试样Fig.1 The demensions of funnel shaped specimen (a)Funnel-shaped specimen of PA66(R=10mm)(b)Funnel-shaped specimen of PA66(R=5mm)
试样夹持段均设计为M25的螺纹连接,利用国家发明专利技术[15]制造的试样对中夹具与MTS试验机连接。对中夹具系统可以有效地消除偏心加载对单轴拉伸试验中的应力、应变、位移测量的影响。
单轴拉伸试验在室温下进行,采用位移控制,拉伸速率为0.005mm/s。每种构形的试样分别进行两次试验,其中漏斗区半径为10mm的试样记为1#试样和2#试样,漏斗区半径为5mm的试样即为3#试样和4#试样。
2 有限元辅助测试试验结果与分析
2.1 FAT方法基本流程
通过单轴拉伸试验,得到两种构形漏斗试样的位移-荷载曲线,根据式(3,4)得到工程应力σE和工程应变σE。
σE=F/A0
(3)
(4)
式中:F为拉伸荷载,A0为拉伸试样的原始横截面积,L0为用于测量拉伸变形的原始标距,L为变形后的试样标距段长度。
根据试验所得载荷-位移曲线,编写ANSYS APDL命令流程序可以实现FAT方法的自动运算,基本流程如下:
(1)完成拉伸试验,根据体积不可压缩理论及Bridgeman修正式(5,6,7)得到可供参考的应力-应变曲线;
(5)
(6)
(7)
其中Fe为弹性当量计长,参考应力和参考应变分别用σr和εr表示,φ是漏斗试样的漏斗区直径,a是漏斗试样中心截面的半径,此公式中的L0与上述不同,表示漏斗试样的漏斗区跨距,H和Ai所代表的变量在图2中给出。
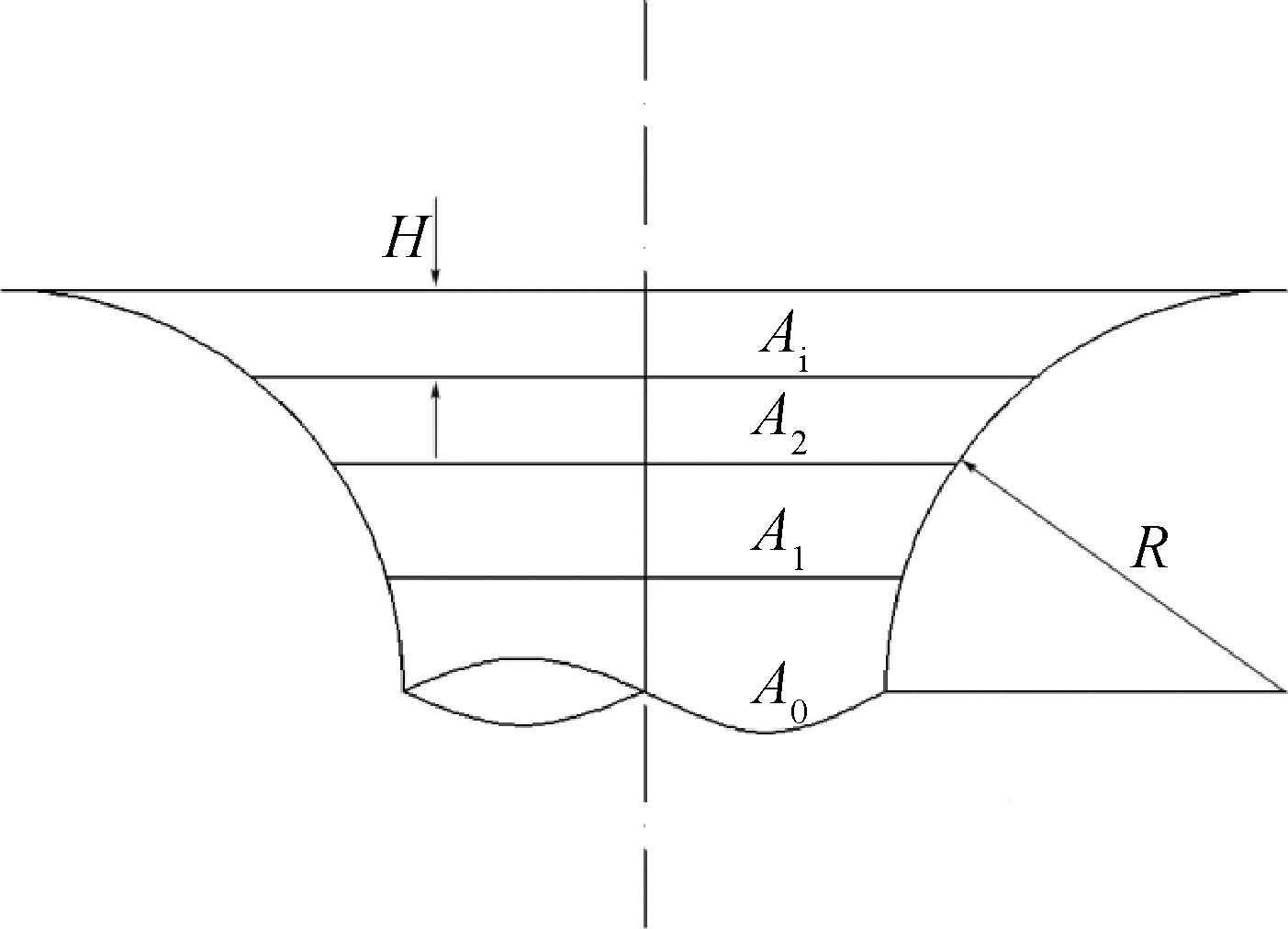
图2 漏斗试样几何参数Fig.2 Geometric parameters of funnel-shaped specimen
(2)建立拉伸试验所用漏斗圆棒试样的有限元
模型,以第(1)步中得到的漏斗试样修正后的参考应力-应变曲线作为有限元分析软件ANSYS材料库中的多线性本构模型进行模拟,从结果中提取试验所用漏斗圆棒试样有限元模型的载荷-位移模拟曲线。
(3)将提取的载荷-位移模拟曲线同第(1)步中的漏斗试样载荷-位移试验曲线进行比较,若二者吻合则停止计算,当前输入的材料本构模型即为被研究材料的真实拉伸全程本构关系,若二者不吻合,则按公式(8)更新ANSYS软件中输入的材料本构模型,其中符号i为迭代的次数,FE为试验原始荷载,FF为模拟输出的荷载,迭代过程中的应力、应变分别由符号σ,ε表示;
(8)
(4)重复第(3)步,直至获得被研究材料的等效全程本构关系时停止迭代计算。
具体流程如图3所示:

图3 FAT方法流程框图Fig.3 The flow chart of FAT method
FAT方法的应用广泛,可用于获取材料直至破断的全程本构关系曲线、破断应力、破断应变、应力三轴度等材料性能,对工程中的结构设计和安全评估具有重要意义。
2.2 采用有限元辅助测试获取试样全程单轴本构关系曲线
按照2.1所述步骤处理聚合物PA66的试验数据,得到两种漏斗试样的载荷-位移曲线和参考应力-应变曲线,如图4所示。
从上图可见,每种构形试样的两组试验曲线基本重合,可见PA66的分散性较小,材料性能稳定。将两种漏斗试样参考应力-应变曲线经Excel筛选拟合后作为有限元分析软件ANSYS材料库中的多线性本构模型进行模拟,利用FAT方法获取聚合物PA66的全程本构关系。鉴于聚合物PA66稳定的力学性能,以下采用1#试样和3#试样的实验数据进行计算和说明。
在软件ANSYS中,由于试样为轴对称结构,对试样1/2剖面建模。建立漏斗区半径R为10mm的试样1/2剖面模型,采用能表征材料塑性大变形的plane183轴对称单元,共包括单元4988个,节点15367个;对漏斗区R为5mm的漏斗试样建模,同样采用plane183单元,模型共包括单元5406个,节点16617个。在利用ANSYS模拟拉伸试验的过程中,两种漏斗试样的模型变形显著,如图5所示。
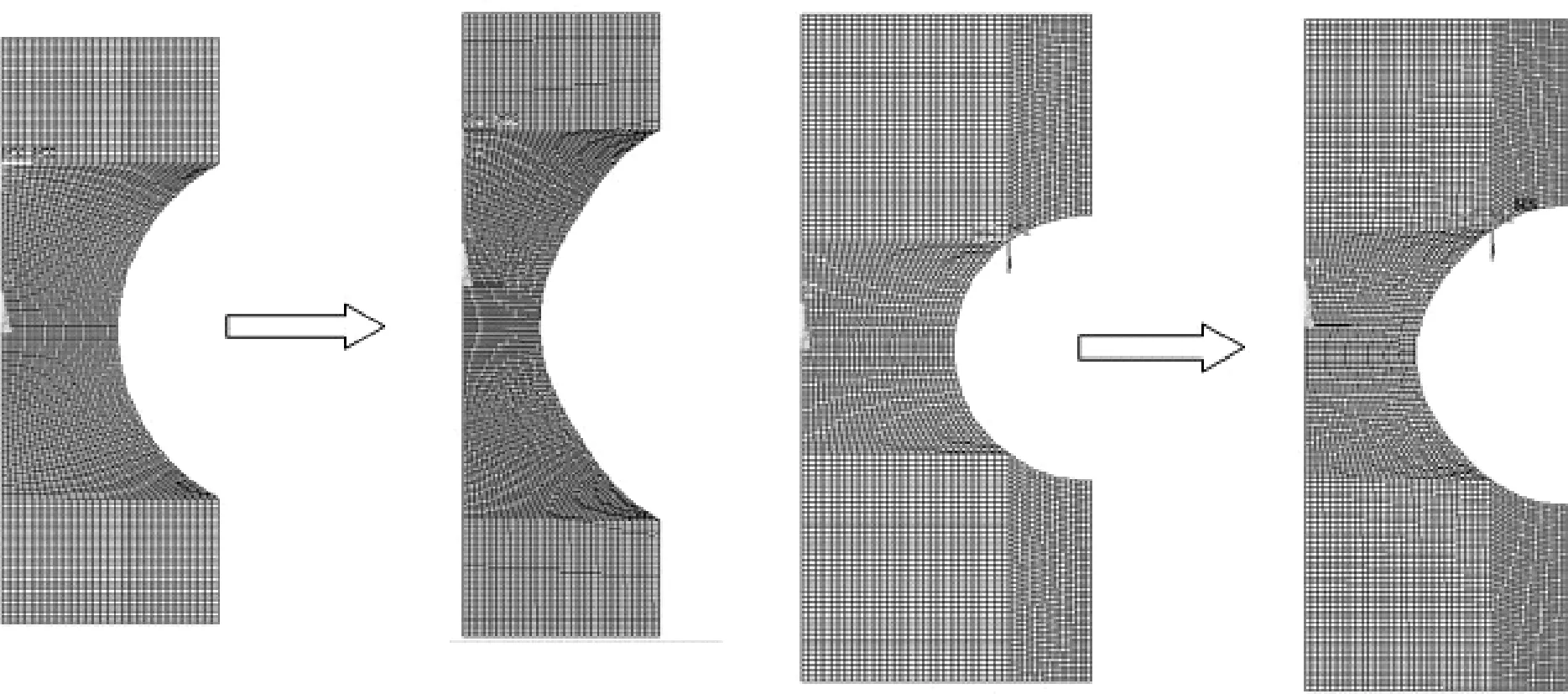
图5 PA66漏斗试样有限元模Fig.5 Finite element model of PA66 funnel-shaped specimen (a) R=10mm;(b)R=5mm
利用FAT方法对漏斗试样单轴拉伸实验数据进行处理,图6、图7所示为两种漏斗试样载荷位移曲线的迭代过程。

图6 PA66试样(R=10mm)1#迭代过程Fig.6 The iterative process of 1# specimen (R=10mm)

图7 PA66试样(R=5mm)3#迭代过程Fig.7 The iterative process of 3# specimen (R=5mm)
从两种漏斗试样迭代过程中的载荷-位移曲线迭代图中可以看出,随着迭代过程的进行,有限元模拟的载荷-位移曲线由最初大量偏离试验曲线到逐渐与试验曲线接近,直至基本重合,此时有限元材料库的应力-应变曲线即为材料的等效全程本构关系曲线。
对比两种漏斗试样通过FAT方法所得的全程本构关系曲线,如图8所示。可以看出,两种漏斗试样的本构关系曲线基本重合,即对于聚合物材料PA66来说,不同构形的漏斗试样通过FAT方法所得的全程本构关系是唯一的,这说明根据FAT方法所获得的PA66全程单轴本构关系是有效的。

图8 PA66试样等效全程本构关系曲线对比Fig.8 The full-range uniaxial constitutive relationship of PA66
2.3 漏斗试样本构关系曲线的Chaboche本构模型
如图9、图10,通过Chaboche本构关系模型,即公式9对聚合物PA66两种漏斗试样的等效全程本构关系曲线进行拟合。
(9)
式中εe和εp分别为弹性应变和塑性应变分量,k为刚发生塑性应变的材料单轴应力,k,R0,R∞,b均为材料常数。
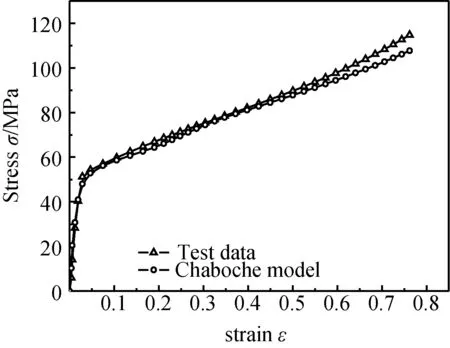
图9 PA66试样(R=10mm)Chaboche模型Fig.9 Chaboche constitutive model of PA66(R=10mm)

图10 PA66试样(R=5mm)Chaboche模型Fig.10 Chaboche constitutive model of PA66(R=5mm)
由上图可见,采用Chaboche模型可以较好的描述PA66的全程本构关系曲线,对应的Chaboche模型参数在表1中给出。

表1 PA66的Chaboche本构模型参数
2.4 破断应力和破断应变结果
将利用FAT方法所得本构关系带入ANSYS软件中,提取试样破断时标距段位移Vf作为位移控制条件进行模拟,得到漏斗试样最大Mises等效破断应力σf和等效破断应变εf,在表2中给出。同时表2中也给出了PA66两种漏斗试样的强度极限Rm和最大载荷处应变εb。
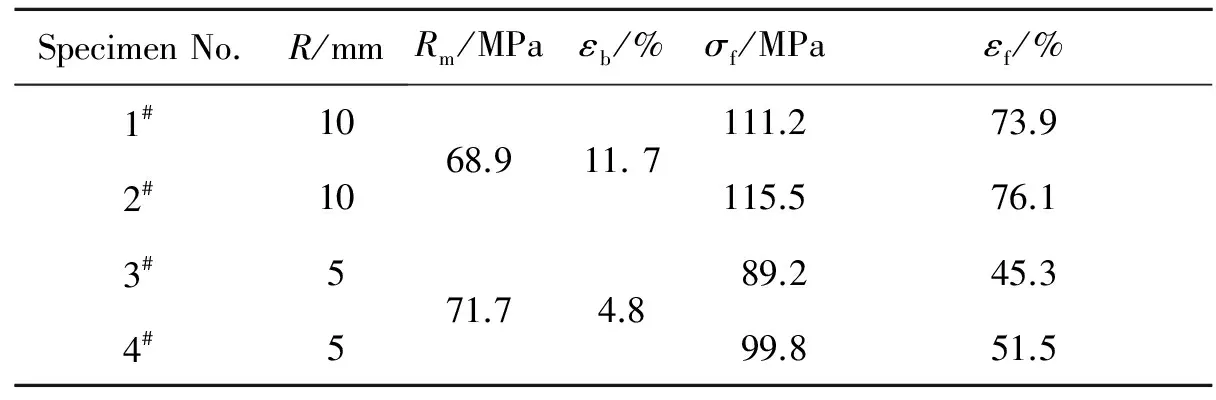
表2 PA66漏斗试样的等效破断应力和破断应变
2.5 应力三轴度的获取
将利用FAT方法所得本构关系带入ANSYS软件中,计算PA66漏斗试样在单轴拉伸情况下漏斗根部的应力三轴度随该点等效应变变化的演化情况,如图11所示。
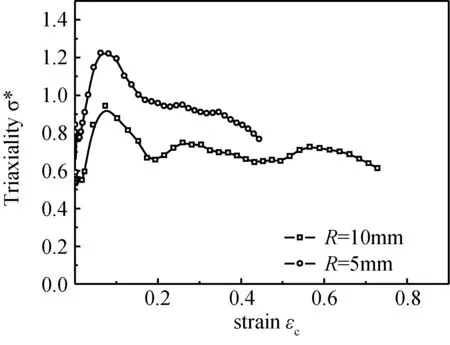
图11 PA66试样漏斗根部应力三轴度演化Fig.11 The evolution of stress triaxiality of PA66
由图11可见,在初始阶段,随着应变提高,对于两种不同构型的试样来说,三轴度均显著提高,随后逐渐降低,即在试验初始阶段,由于缺口效应,材料内部出现复杂的应力状态,此时三轴度表现较为显著,随着加载进程,材料逐渐进入大变形阶段,逐渐显著提高的塑性变形使得漏斗试样根部曲率和应力重分布发生显著变化,从而引起了三轴度下降;图11还可以表明试样的漏斗区半径越小,三轴度效应越突出,且破断应变也相应减小。
基于有限元对PA66漏斗试样漏斗根部横截面临界时在临界破断时的应力三轴度分布情况进行了分析,图12所示为试样漏斗根部横截面临界时的应力三轴度分布情况,其中横坐标为漏斗根部横截面上的节点到横截面中心点的距离X与横截面半径R之比,可见,漏斗根部横截面中心处的应力三轴度状态远高于其边界处,即可以说明对应三轴度最高的漏斗根部横截面中心是拉伸破坏的初始破坏源。图11、12还可表明试样的漏斗区半径越小,三轴度效应越突出,且破断应变也相应减小,进而表明三轴度效应是制约破断发生的重要原因。
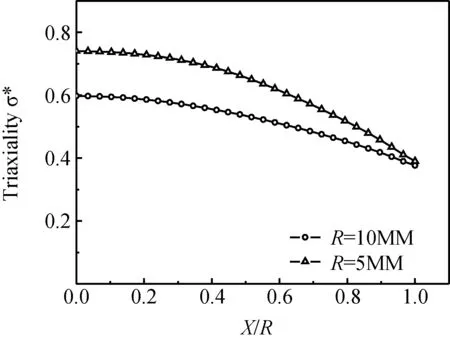
图12 PA66试样漏斗根部横截面临界破断时应力三轴度分布情况Fig.12 The stress triaxiality distribution on the fracture surface of PA66 funnel shaped specimen
2.6 试样破断面的应力分布
将FAT方法所得聚合物PA66本构关系带入ANSYS软件中进行模拟,获取聚合物PA66漏斗试样最小截面上临界破断时的应力分布情况,如图13所示。
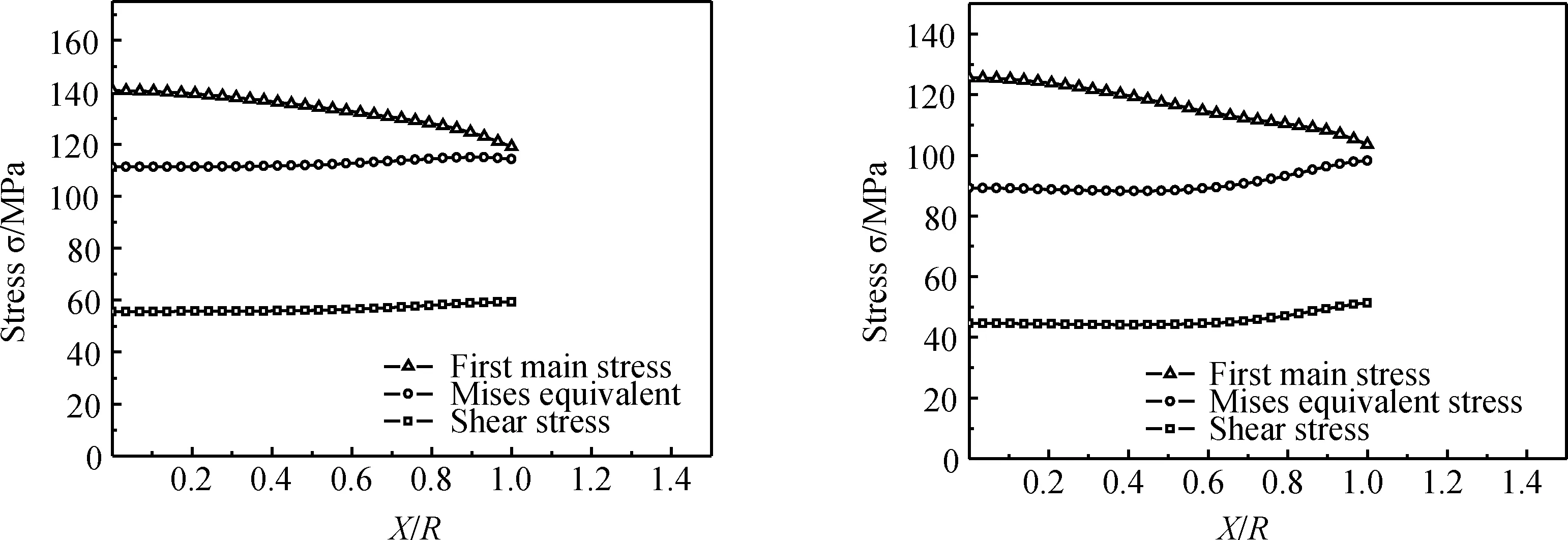
图13 PA66试样破断面应力分布 (a)PA66试样(R=10mm)1#颈缩截面应力分布; (b)PA66试样(R=5mm)3#颈缩截面应力分布Fig.13 The stress distribution on the fracture surface of PA66 funnel shaped specimen (a)The stress distribution in necking cross section of PA66(R=10mm) before breaking;(b)The stress distribution in necking cross section of PA66(R=5mm) before breaking
从上图中可以看出,Mises等效应力和切应力在试样最小横截面上均匀分布,即Mises等效应力和切应力对试样断裂的影响较小。而第一主应力从试样中间到边缘逐渐降低,所以第一主应力在聚合物PA66的破断过程中起主要作用。
结合2.5中结果,因为颈缩截面处的应力三轴度与第一主应力分布规律相同,所以应力三轴度和第一主应力在破断中起主要作用,且由推测可知,延性材料聚合物PA66在高约束下发生脆性断裂,初始破断发生在漏斗根部的横截面中心,第一主应力在此断裂中起主要作用,初始破断后,试样内部整体约束降低,此后,Mises等效应力控制断裂行为。因此,在拉伸试验的破断分析中,第一主应力和Mises等效应力在不同位置、不同阶段分别控制破断行为的发生。聚合物PA66的断口形态在图14中给出。
2.7 VIC-3D系统测试结果与FAT方法计算结果比较
PA66拉伸试验进行的同时,采用VIC-3D光学测试系统对试验进行辅助测试。初始时两种漏斗构形试样表面未发生形变,应变为零。经计算分析可以得出试样破断时表面的应变分布云图,将两种漏斗试样发生破断时表面的轴向应变分布云图与通过FAT方法所得本构关系作为ANSYS软件材料库中的多线性本构模型进行模拟输出的应变分布云图对比,如图 15和图16所示。

图14 PA66试样拉伸后断口形态Fig.14 The fracture morphology of the funnel-shaped specimen after the tensile test

图15 PA66试样(R=10mm)表面应变光测与有限元计算结果比较Fig.15 The strain results comparision of optical testing and finite element calculation on the surface of the funnel-shaped specimen (R=10mm)

图16 PA66试样(R=5mm)表面应变光测与有限元计算结果比较Fig.16 The strain results comparision of optical testing and finite element calculation on the surface of the funnel-shaped specimen (R=5mm)
由上图可见,两种计算方法所得结果十分接近,应变之间的最大误差小于6%。光测方法所得结果可以进一步论证FAT方法在求解聚合物PA66全程本构关系时的可行性和有效性。
3 结论
(1)针对两种漏斗半径(R=10mm和R=5mm)的PA66材料试样进行了准静态室温拉伸试验,根据拉伸试样的P-V试验结果并结合FAT方法获得了试样颈缩阶段的等效单轴本构关系(式9),给出了PA66材料直到破坏的Chaboche本构模型参数(k,R0,R∞,b见表1)、破断应力σf、破断应变εf(表2);
(2)利用VIC-3D光学测试设备证明了FAT方法对于求解聚合物PA66全程本构关系的普适性和精确性;
(3)根据Chaboche全程本构模型,基于有限元分析,研究了试样漏斗根部横截面的应力三轴度σ*的分布与演化规律,揭示出对应三轴度最高的漏斗根部横截面中心是拉伸破坏的初始破坏源,且三轴度效应越突出,破断应变越小,试样中心因三轴度更高而先行发生破坏。
[1] BRIDGMAN P W. Studies in Large Plastic Flow and Fracture[M]. London:Harvard University Press,1952.
[2] EDUARDO E. CABEZAS, CELENTANO DIEGO J. Experimental and numerical analysis of the tensile test using sheet specimens[J]. Finite Element in Analysis and Design ,2004,40(5):555-575.
[3] ZHANG K S. Technical note fracture prediction and necking analysis [J].Engineering Fracture Mechanics,1995,52(3):575-582.
[4] BRIINIG M. Numerical analysis and modeling of large deformation and necking behavior of tensile specimens [J]. Finite Elements in Analysis and Design,1998,28:303-319.
[5] DUMOULIN S, TABOUROT L, CHAPPUIS C. Determination of the equivalent stress-quivalent strain relationship of a copper sample under tensile loading [J]. Journal of Materials Processing Technology,2003, 133:79-83.
[6] MANSOO J, EOMC J G, LEE M C. A new method for acquiring true stress-strain curvesover a large range of strains using a tensile test and finite element method [J]. Mechanics of Materials, 2008,40(7):586-593.
[7] 陈辉,蔡力勋,姚迪,等. 基于小尺寸材料试验与有限元分析的耦合方法获取材料力学性能[J].机械强度,2014,36(2):187-192.
(Chen H,CAI L X,YAO D,etal. Obtaining material mechanical properties by coupling method based on tests of small size specimens and finite element analysis[J]. Journal of Mechanical Strength, 2014,36(2):187-192.
[8] 姚迪,蔡力勋,包陈,等. 基于试验与有限元耦合技术的延性材料全程单轴本构关系获取方法[J].固体力学学报,2014,35(3):226-240.
(YAO Di,Cai L X,BAO C,etal. Determination of stress-strain curves of ductile materials by testing and finite element coupling method[J]. Chinese Journal of solid mechanics, 2014, 35(3):226-240.)
[9] SIMO J. Numerical analysis and simulation of plasticity[J]. Handbook of numerical analysis, 1998, 6: 183-499.
[10]WRIGGERS P, MIEHE C, KLEIBER M,etal. On the coupled thermo-mechanical treatment of necking problems via finite-element-method [J].Proceedings of COMPLAS II, 1989, 527-542.
[11]SIMO J, ARMERO F. Geometrically non-linear enhanced strain mixed methods and the method of incompatible modes [J]. International Journal for Numerical Methods in Engineering,1992, 33:1413-1449.
[12]ARMERO F, SIMO J.A priori stability estimates and unconditionally stable product formula algorithms for non-linear coupled thermo plasticity [J]. International Journal ofPlasticity, 1993(9):149-182.
[13]肖华明,罗文波.PA6/PTEE和PA66/PTEE的力学性能和熔融行为的实验研究[J].湖南工程学院学报,2006,16(3):38-41.
(XIAO H M, LUO W B. Experimental studies on mechanical properties and melting behaviors of PA6 /PTFE and PA66 /PTFE blends[J]. Journal of Hunan Institute of Engineering,2006(9),16(3):38-41.
[14]姚迪,蔡力勋. 小曲率漏斗试样获取材料全程单轴本构关系的TF方法[J].四川大学学报(工程科学版),2012,44:163-166.
(YAO D, CAI L X. An approach for full-range uniaxial constitutive relationship of 304 stainless steel [J].Journal of Sichuan university(Engineering science edition), 2012, 44:163-166.
[15]蔡力勋,姚迪,包陈. 单轴拉伸全程真应力-真应变测试技术: 中国,201110152281[P]. 2011-10-19.
(CAI L X, YAO D, BAO C. Testing technology of the full-range uniaxial true strain-stress: Chinese invention patent,201110152281[P]. 2011-10-19.)
Full-range Uniaxial Constitutive Relationship up toFailure of Polymer PA66
YU Si-miao1, CAI Li-xun1, ZHAO Guo-ming2
(1.School of Engineering and Mechanics, Southwest Jiaotong University, Chengdu 610031, China; 2. Laboratory and Equipment Management of SWJTU, Chengdu 610031, China)
Polymers have been widely used in various structural engineering, and the importance of relevance to their fracture properties and full-range constitutive relationships up to failure is attached recently. The accurate full-range constitutive relationships up to failure are important for light structure design and safety assessment. Based on finite-element-analysis aided testing(FAT) method[1], the full-range uniaxial constitutive relationship of PA66 is investigated. Meanwhile, the strain distribution field on the surface of funnel-shaped specimen is tested by the DIC (Digital image correlation) optical measurement system. Comparing the testing results with the finite element simulating results by FAT, both of them are coincided well. So it is accurate for FAT to obtain the full-range uniaxial constitutive relationship of PA66. As results, for PA66, the parameters of Chaboche constitutive relationship model, critical breaking stress, critical breaking strain, stress triaxiality of polymer material PA66 are obtained, and also the fracture behavior of those specimens were discussed.
polymer materials PA66; the full-range uniaxial constitutive relationship; finite element aided testing-FAT method; DIC optical measurement system
2014-06-27;
2014-11-12
国家自然科学基金(11472228);西南交通大学重点实验室开放项目
蔡力勋(1959—),男,教授,主要从事材料破坏与结构安全研究,(E-mail) lix_cai@263.net。
10.11868/j.issn.1005-5053.2015.3.011
TB324
A
1005-5053(2015)03-0060-09

