差动轮系中的循环功率分析

贺亮　叶斯伦　张庆春等

摘 要：通过分析典型的差动轮系中齿轮受力与转速的关系，推导出差动轮系中当2个不同构件作主动件时的2种典型工况下，轮系产生循环功率的条件和原因，并采用某液压机械无级变速箱中的双排差动轮系的工作实例进行了分析和验证。研究结果表明，差动轮系中是否产生循环功率取决于2个主动构件的转动方向。该结论可以为采用差动轮系传递动力的系统提供理论参考依据，使系统避免工作在产生循环功率的工况下，提高系统的工作效率。

关键词：差动轮系；转速；转矩；循环功率

中图分类号 U463.212 文献标识码 A 文章编号 1007-7731（2015）11-121-04

Abstract：The relation between gears' stress and rotating speed were analyzed when use two different parts as power input member，and condition when cycle power produced in differential gear train system were obtained in two typical working conditions.A kind of hydro-mechanical continuously variable transmission（HMCVT）with double row differential gear train was analyzed to verify the conclusions.The results showed that whether recycle power was produced depends on the two active members' relative rotating directions.The conclusion provided theoretical reference for a system with a differential gear train to avoid producing cycle power and improving the work efficiency.

Key words：Differential gear train system；Rotating speed；Torque；Cycle power

1 引言

差动轮系是一个二自由度齿轮系统，具有2个主动构件作为能量输入元件，由于其传动比较大，经常被使用在双输入单输出的传动系统中。在农业机械中，差动轮系经常被应用到液压机械无级变速箱中，用于耦合液压动力和机械动力[1-4]。但是若差动轮系中的2个主动齿轮输入特定的转速和转向时，有可能会使2个主动齿轮输入齿轮系统中的功率发生抵消而出现循环功率[7，9]，导致差动轮系中的内部消耗的功率急剧增加，使系统输出功率明显降低，系统总效率也明显降低，对传动十分不利[5-11]。因此，在传动系统中使用差动轮系，特别是系统传动较大功率时，应避免差动轮系出现循环功率[12-16]。本研究对差动轮系中产生循环功率的原因进行了分析，总结和归纳了差动轮系的产生循环功率时的特征，从而为提高差动轮系的传动效率提出指导性的意见和建议。

2 差动轮系的输出功率分析

一个典型的差动轮系模型如图1所示，轮系由中心轮1、行星轮2、中心轮3以及行星架H组成。根据不同构件作为主动构件的情况，可以将轮系分为4种不同工况，并且分析轮系中功率的传递情况。2种典型传动工况分别如下：（1）2个中心轮1和3作为主动构件，且中心轮1、3同向或反向转动；（2）其中一个中心轮和行星架H作为主动构件同向转动及反向转动。当以其中一个中心轮和行星架作为主动构件时，以中心轮1或中心轮3为主动构件的分析方法一样，因此本文仅分析以中心轮1作为主动构件的情况，中心轮3作为主动构件的情况类似。

2.1 中心轮1和中心轮3作为主动构件 当中心轮1、3作为主动构件时，行星架H作为输出构件输出功率。功率传动路线如下，中心轮1、3输入功率，驱动行星轮2转动，行星轮2再将功率传至行星架H上，再由行星架H将功率输出。

若中心轮1输入转速n1沿逆时针转动，且中心轮3的转动方向n3与中心轮1的转动方向相同，当该齿轮系中各齿轮保持恒定转速时，行星轮2的受力如图2所示，对行星轮2在图2所示位置列水平方向受力平衡公式，得[F12+F32=FH2]。

根据式（2），若中心轮1的转速n1与中心轮3的转速n3转动方向相同时，[n1+Z3Z1n3]和[F12+F32]同时达到最大值，行星架的输出功率PH达最大值。此时，若不考虑齿轮系统中的摩擦功率损失，行星架的输出功率应该等于中心轮1和中心轮3的输入功率之和，即[pH=p1+p3]，该齿轮系统中没有循环功率产生。

若中心轮1的转速n1与中心轮3的转速n3转动方向相反时，[n1+Z3Z1n3]和[F12+F32]同时达到最小值。此时，若不考虑齿轮系统中的摩擦功率损失，行星架的输出功率应该等于中心轮1和中心轮3的输入功率之差，即[PH=P1-P3]，该齿轮系统中产生循环功率。循环功率[Pre=2?min（P1，P3）]，即中心轮1和中心轮3的输入功率相互抵消，产生循环功率，其大小为2个主动件中输入功率较小量的2倍。

2.2 中心轮1和行星架H作为主动构件 中心轮1和行星架H作为主动构件时，中心轮3作被动件输出功率。功率传动路线如下，中心轮1和行星架H输入功率，驱动行星轮2转动，行星轮2再将功率传至中心轮3上，由中心轮3输出功率。

若中心轮1输入转速n1沿逆时针转动，且齿轮1和行星架H的转动方向相同，当该齿轮系中各齿轮保持恒定转速时，行星轮2的受力如图3所示，对行星轮2在图2所示位置列水平方向受力平衡公式，得[F12+F32=FH2]；对行星轮2的中心列力矩平衡公式，得[F12?r2+F32?r2=0]，即[F12+F32=0]，从而可知[F12=F32=FH2/2]。

根据式（4），若中心轮1的转速n1与行星架H的转速nH转动方向相同时，[（1+Z3Z1）nH-n1]达到最小值，并且[F32]取决于外界输入功率的大小，与输入轮的转速无关，因此，行星架的输出功率PH达最小值。此时，若不考虑齿轮系统中的摩擦功率损失，行星架的输出功率应该等于中心轮1和行星轮H的输入功率之差，即[P3=P1-PH]，该齿轮系统中产生循环功率。循环功率[Pre=2?min（P1，PH）]，即中心轮1和行星架H的输入功率相互抵消，产生循环功率，其大小为2个主动件中输入功率较小量的2倍。

若中心轮1的转速n1与行星架H的转速nH转动方向相反时，[（1+Z3Z1）nH-n1]达到最大值，并且[F32]取决于外界输入功率的大小，与输入轮的转速无关，因此，行星架的输出功率PH达最大值。此时，若不考虑齿轮系统中的摩擦功率损失，行星架的输出功率应该等于中心轮1和中心轮3的输入功率之和，即[pH=p1+p3]，该齿轮系统中没有循环功率产生。

3 实例分析

图3是某型号200马力拖拉机液压机械无级变速箱（Hydro-mechanical continuously variable transmission，HMCVT）的结构简图[1]，该变速箱采用双排行星汇流式结构耦合机械和液压动力。1轴为机械动力输入轴，2轴为液压动力输入轴，3轴为动力输出轴，C1、C2、C3、C4是离合器。为了获得连续的输出，变速箱需要适时结合不同的离合器，并且通过变量泵需要输出不同的转向和大小的转速，以获得连续增加的输出转速。当C1或C3离合器接合时，右排差动轮系K2起作用，主动轮是中心轮1和中心轮3，右排差动轮系K2中的行星架H输出功率；当C2或C4离合器接合时，左排差动轮系K1起作用，主动轮是中心轮1和行星架H，左排差动轮系K1中的中心轮3输出功率。因此，在4个离合器分别结合时，在每种工况下总会产生循环功率，在工作过程中应尽量越过该工作段。k1、k2分别为K1、K2行星轮系中内齿圈齿数与小中心轮齿数之比，该变速箱中k1、k2分别为2.56、3.56；各齿轮副传动比如下：i1=1.44、i2=0.97、i3=1.48、i4=0.67、i5=1.96、i6=1.02、i7=3.52、i8=2.77、i9=0.79、i10=2.77、i11=0.82、i12=1.09。发动机在经济燃油消耗点工作，输出转速为1 500r/min。由于当离合器C1结合时，变速箱输出转速较低，变量泵的排量比变化范围为-0.6～1，其余档位变量泵排量比变化范围为-1～1。因此，本研究中采用离合器C2和C3分别结合时的工作情况进行分析。根据试验结果可知机械输入轴和液压输入轴的输入转速和功率如表1、2所示。

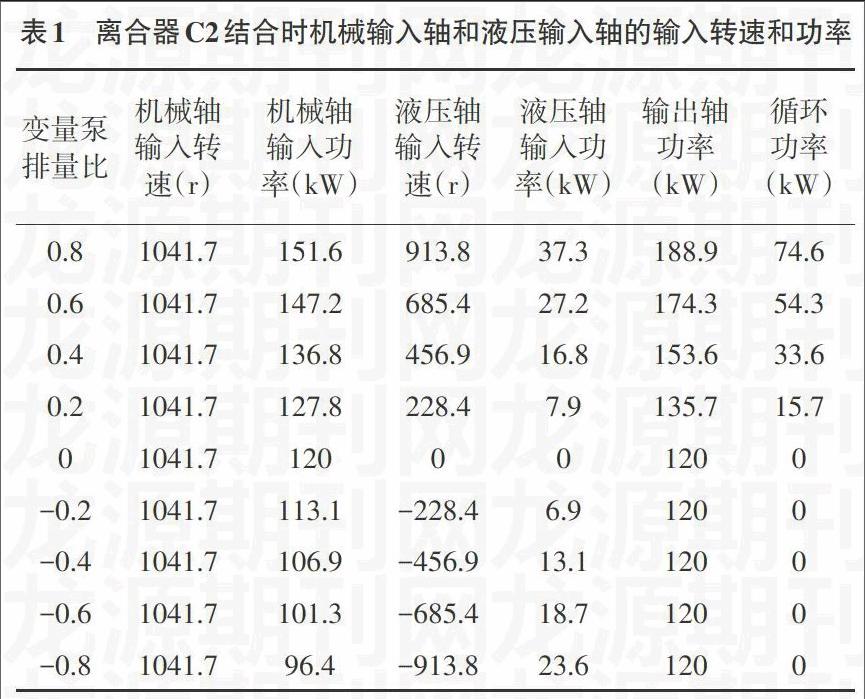
从表1可以看出，当C2离合器接合，差动轮系中主动轮是中心轮1和行星架H，左排差动轮系K1中的中心轮3输出功率。随着变量泵的排量比从0.8逐渐减小至0时，液压轴输入转速从正向的913.8rpm逐渐减小至0，此时，液压轴输入转速的方向与机械轴输入转速方向相同，系统产生循环功率，且循环功率的大小始终为液压轴输入功率的2倍；随着变量泵的排量比从0逐渐变化至-0.8时，液压轴输入转速从的0逐渐变化至反向913.8rpm，此时，液压轴输入转速的方向与机械轴输入转速方向相反，系统不产生循环功率。

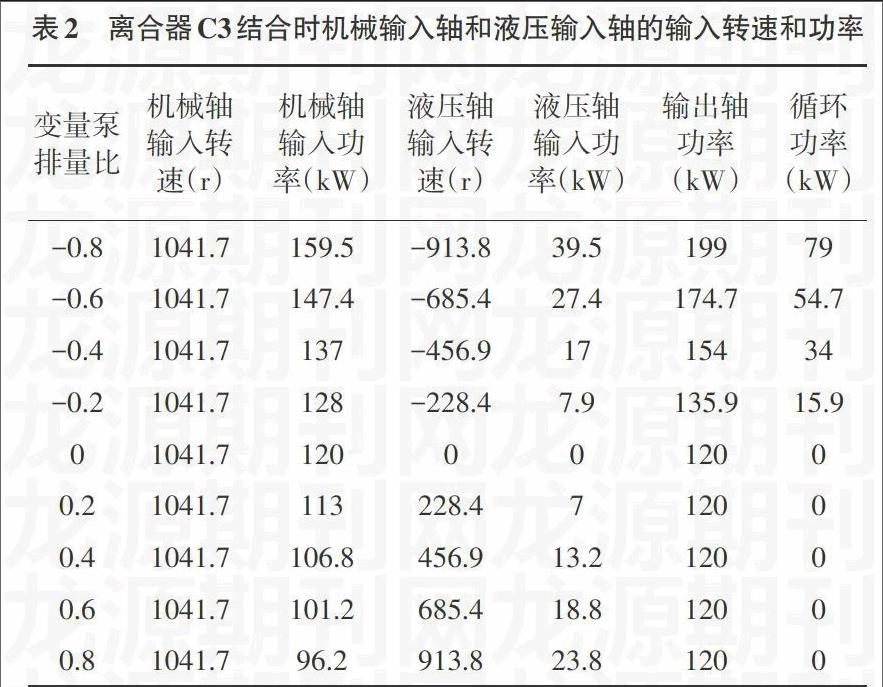
从表2可以看出，当C3离合器接合，差动轮系中主动轮是中心轮1和中心轮3，右排差动轮系K2中的行星架H输出功率。随着变量泵的排量比从-0.8逐渐变化至0时，液压轴输入转速从反向的913.8rpm逐渐减小至0，此时，液压轴输入转速的方向与机械轴输入转速方向相反，系统产生循环功率，且循环功率的大小始终为液压轴输入功率的2倍；随着变量泵的排量比从0逐渐增大至0.8时，液压轴输入转速从的0逐渐变化至正向913.8rpm，此时，液压轴输入转速的方向与机械轴输入转速方向相反，系统不产生循环功率。

4 结论

差动轮系中2个不同构件作主动件时，差动轮系中是否产生循环功率取决于2个主动构件的转动方向，2种典型工况下，是否产生循环功率的归纳如下：（1）中心轮1和中心轮3作主动构件输入功率，行星架H作被动件输出功率时，当轮1和轮3的转速方向相同时，不产生循环功率；当轮1和轮3的转速方向相反时，产生循环功率。（2）中心轮1和行星架H作主动构件输入功率，中心轮3作被动件输出功率时，当轮1与行星架H的转速方向相同时，产生循环功率；当轮1与行星架H的转速方向相反时，不产生循环功率。（3）当差动轮系中产生的循环功率时，循环功率的数值为是2个输入构件中传递功率较小量的2倍。

研究结论可以为采用差动轮系传递动力的系统提供理论参考依据，使系统避免工作在产生循环功率的工况下，提高系统的工作效率。

参考文献

[1]王光明，朱思洪，史立新，等.拖拉机液压机械无级变速箱效率特性的仿真与试验[J].农业工程学报，2013，15：42-48.

[2]M.Schulz，谷雨.动力换档混合电动车辆变速箱内的循环机械功率[J].传动技术，2006，02：23-29.

[3]徐立友，周志立，张明柱，等.拖拉机液压机械无级变速器的特性分析[J].中国农业大学学报，2006，05：70-74.

[4]侯增源.液压-机械分流传动循环功率流分析[J].上海海运学院学报，1993，02：28-33.

[5]吕海涛，孔江生，王建民.行星传动变速箱功率流及循环功率分析法[J].煤矿机械，2004，06：40-41.

[6]苏志霄，薛隆泉，崔亚辉，等.封闭式行星轮系传动效率计算的结点功率法[J].机械科学与技术，1996，05：81-85.

[7]崔松竹，程岭.组合式无级变速器的循环功率流分析[J].沈阳工业学院学报，1996，01：6-14.

[8]李庆凯，唐德威，姜生元，等.封闭式行星轮系功率流判别的键合图法[J].北京航空航天大学学报，2012，09：1250-1254.

[9]刘开昌，吴云杰.封闭式锥盘无级变速器无循环功率条件及应用[J].郑州大学学报（工学版），2012，06：84-87.

[10]卢存光，段钦华，杨实如.封闭式行星传动功率流分析与啮合效率计算[J].机械传动，2002，02：36-38.

[11]黄启林.封闭式行星齿轮传动系统动态特性研究[D].济南：山东大学，2014.

[12]董万福，吴斌，段钦华.封闭式行星轮系的结构与功率流研究[J].机械设计与研究，2007，03：82-83，112.

[13]卢存光，段钦华.封闭式行星轮系中功率流的图解法[J].机械传动，2007，06：76-77.

[14]舒约文.封闭式行星轮系的效率[J].机械科学与技术，1994，03：73-74.

[15]杨兰生，汪仁树.关于行星轮系效率计算通用程序的研究[J].哈尔滨科学技术大学学报，1986，01：1-14.

[16]张恒新.复杂行星齿轮机构的封闭循环功率计算[J].起重运输机械，1984，11：21-26. （责编：张宏民）