几乎可数仿紧空间的性质与刻画

蔡奇嵘, 刘唐伟

(东华理工大学 理学院, 江西 南昌 330013)



几乎可数仿紧空间的性质与刻画

蔡奇嵘, 刘唐伟

(东华理工大学 理学院, 江西 南昌 330013)

在Elise Grabner定义几乎亚紧空间的基础上，引入了几乎可数仿紧空间，得到了一个关于它的等价刻画定理：X为几乎可数仿紧空间当且仅当X的每个可数散射分解有一个几乎局部有限的开膨胀。讨论了几乎仿紧空间、几乎可膨胀空间、几乎可数仿紧空间三者之间的关系：几乎κ-仿紧空间是几乎κ-可膨胀的。空间X是几乎可数仿紧的当且仅当X是几乎可数可膨胀的。

几乎可数仿紧；几乎可膨胀；几乎局部有限；散射分解

蔡奇嵘, 刘唐伟.2015.几乎可数仿紧空间的性质与刻画[J].东华理工大学学报：自然科学版，38(4)：458-460.

Cai Qi-rong,Liu Tang-wei.2015.Properties and characterization of nearly countable paracompact spaces[J].Journal of East China Institute of Technology (Natural Science), 38(4)：458-460.

广义仿紧空间理论研究是一般拓扑学中很重要的研究课题之一。Grabner等(1999)定义了几乎亚紧(亚lindelÖf)空间的概念，并给出了它的一个刻画，得到了几乎亚紧空间是紧空间的两个充分条件。曹金文(2003)又引入了几乎仿紧空间，获得了无限个因子的Tychonoff积的两个等价定理，还给出了几乎仿紧空间的一个刻划。本文在此基础上，引入了几乎可数仿紧空间，对它的有关性质作了初步的探讨。

本文用N表示自然数集，(ξ)x和N(x)分别表示集族{U∈ξ∶x∈U}和点x的邻域系；(ξ)G表集族{U∈ξ∶U∩G≠∅}；St(G,ξ)=∪(ξ)G；|∑|表示集合∑的基数；ω表示非负整数集，也表示第一无限序数；ClA和IntA分别表示集合和闭包和内部。本文所涉及的所有拓扑空间都假设为Hausdorff空间，并且简称拓扑空间为空间，采用的记号及引用的结论，如不声明，均与Engelking(1997)，蒋继光(1991)相同。

1 预备知识

定义1 设λ是一个基数,并且λ≥2,空间X称为是λ-仿紧的,如果X的每个≤λ势的开覆盖有一个局部有限的开加细(蒋继光，1991)。

定义2 空间X称为是几乎仿紧的当且仅当X的每个开覆盖U，都存在X的一个稠密子集D和U的开加细η，对任意x∈D，存在o∈N(x)，使得(η)o是有限的(曹金文，2003)。

定义3 空间X的一个散射分解是指X的两两不相交的子集构成的覆盖{Lα∶α<γ}并且满足∀α<γ，∪{Lδ∶δ<γ}开于(Junnila et al.,1986)。

2 关于几乎可数仿紧空间

2.1 相关的概念

定义4 设ξ是空间X的一个子集族，称ξ在空间X内是几乎局部有限的，如果存在X的一个稠密子集D，对任意x∈D，存在o∈N(x)，使得(ξ)o是有限的。

定义5 设ξ={Uα∶α<γ}是空间X的一个子集族，称ζ={Vα∶α<γ}是ξ在X中具有几乎局部有限的开膨胀，如果满足条件：

⑴ζ在空间X内是几乎局部有限的开集族。

⑵对任意α<γ，Uα⊂Vα。

定义6 设基数κ≥ω，空间X称为是几乎κ-仿紧的当且仅当X的每个势≤κ的开覆盖U，都有几乎局部有限的开加细。

几乎ω-仿紧空间又称为是几乎可数仿紧空间。

定义7 ⑴ 设基数κ≥ω，空间X称为是几乎κ-可膨胀的当且仅当X的每个局部有限的闭集族{Fα∶α<κ}，都存在X的几乎局部有限的开集族U={Uα∶α<κ}，且对任意α<κ，Fα⊂Uα。

几乎ω-可膨胀空间又称为是几乎可数可膨胀空间。

⑵ 空间X是几乎可膨胀的，如果对任意κ≥ω，X是几乎κ-可膨胀的。

2.2 主要结论

定理1 若空间X的开覆盖ξ={U(s)∶s∈S}有几乎局部有限的开加细η，则ξ有一个几乎局部有限的精确开加细。

证明：设η={Vt∶t∈T}，对任意Vt∈η，存在s(t)∈S，使Vt⊂U(s(t))，对任意s∈S，令W(s)=U{Vt∈η∶s(t)=s}，下证{W(s)∶s∈S}为ξ的几乎局部有限的精确开加细。事实上，因为η={Vt∶t∈T}几乎局部有限，所以存在X的一个稠密子集D，对任意x∈D，存在U∈N(x)，使得(η)o是有限的。即存在有限集T0⊂T，使得对任意t∈TT0，有U∩Vt=∅，

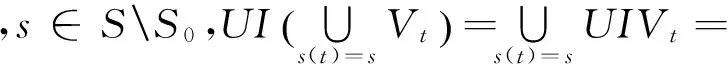
所以{W(s)∶s∈S}为ξ={U(s)∶s∈S}的几乎局部有限的精确开加细。

定理2 X为几乎可数仿紧空间当且仅当X的每个可数散射分解有一个几乎局部有限的开膨胀。

证明： 充分性，设{Ln∶n∈N}是X的任意可数散射分解，令Un=∪{Lk∶k≤n}，则{Un∶n∈N}是X的一个开覆盖，由定理1知，其存在X中几乎局部有限的精确开加细{Vn∶n∈N}，存在X的一个稠密子集D和U，对任意x∈D，存在O∈N(x)，使得|{Vn∶O∩Vn≠∅,n∈N}是有限的，令Wn=∪{Vk∩Un∶k≥n}。

设i(x)=max{n∈N∶O∩Vn≠∅}，则对任意j>i(x)，∪k>jVk∩O=∅，由于Wn⊂∪{Vk∶k≥n}，则{Wn∶n∈N}也是X中几乎局部有限的。由于{Ln∶n∈N}是X的散射分解，所以对任意i∈N,n

Li⊂∪{Vk∩Li∶k≥i}⊂∪{Vk∩Li∶k≥i}=Wi，

所以{Wn∶n∈N}是{Ln∶n∈N}在X中几乎局部有限的开膨胀。

定理3 几乎κ-仿紧空间是几乎κ-可膨胀的。

定理4 空间X是几乎可数仿紧的当且仅当X是几乎可数可膨胀的。

证明： 充分性，由定理3可知。

必要性，设ζ={Un∶n∈N}为几乎可数可膨胀空间X的可数开覆盖。令E0=U0，对n≥1，En=Un∪i

由定理3与定理4可得以下结论：

推论1：几乎仿紧空间是几乎可膨胀的，几乎可膨胀空间是几乎可数仿紧的。

曹金文. 2003.几乎仿紧空间[J].纯粹数学与应用数学,19(1):57-60.

蒋继光. 1991.一般拓扑学专题选讲[M].成都:四川教育出版社.

苏淑华,许兆龙,许志军.2008.拓扑分子格的直和及其性质[J].东华理工大学学报:自然科学版,31(3):298-300.

苏淑华,张美英,许兆龙.2009.LF拓扑空间的强正则闭分离性[J].东华理工大学学报:自然科学版,32(2):197-200.

许兆龙. 2006.拓扑分子格的S紧化与S次紧化[J].东华理工学院学报,29(1):92-96.

Eengelking R. 1977.General Topology[M]. Warszawa:Polish Scientific Pulishers.

Grabner E, Grabner G. 1999. Nearly metacompact spaces[J]. Topology Appl.,98: 191-201.

Junnila H J,Smith J C,Telagarsk R.1986.Closure-preserving covers by small sets[J]. Topology Appl., 23:237-262.

Properties and Characterization of Nearly Countable Paracompact Spaces

CAI Qi-rong, LIU Tang-wei

(School of Science, East China Institute of Technology, Nanchang, JX 330013, China)

The notion of nearly countable paracompact spaces on the basis of Elise Grabner defined nearly metacompact spaces are introduced, get a equivalent characterization:Xis a nearly countable paracompact space if and only if every scattered partition ofXhave a nearly locally finite open expansion. And also discuss of the relationship between nearlyκ-paracompact spaces, nearly countable paracompact spaces and nearlyκ-expandable spaces:Nearlyκ-paracompact space is a Nearlyκ-expandable space.Xis a nearly countable paracompact space if and only ifXis a nearly countable expandable space.

nearly Countable paracompact; nearly expandable; nearly locally finite; scattered patition.

2014-09-02

江西省自然科学基金资助项目(20114BAB201016)；江西省教改基金资助项目(JXJG-11-8-21)

蔡奇嵘(1982—),女,硕士,讲师，主要从事一般拓扑学的研究。E-mail：qrcai@ecit.cn

10.3969/j.issn.1674-3504.2015.04.020

O189.11

A

1674-3504(2015)04-0458-03