强制循环蒸发系统线性自抗扰解耦控制的鲁棒设计

张园，孙明玮，陈增强

（南开大学计算机与控制工程学院，天津300071）

引 言

强制循环蒸发系统是蒸发工序的重要组成部分［1］，其目的是消除溶液中的有机杂质，产生满足工艺需求的产品。为了提高蒸发效率，产品密度必须快速地跟踪工艺设定值；为了保证系统平稳安全地运行，溶液液位必须保持稳定，避免大幅度波动。

由于强制循环蒸发系统固有的复杂动力学特性，液位回路和产品密度回路具有高度非线性和耦合性，因此，研究强制循环蒸发系统的解耦控制具有重要意义［2－3］。目前文献报道中的许多解耦方法，如对角矩阵法［4］、特征轨迹法［5］以及自适应解耦控制法［6］等，都是针对线性系统设计的，难以应用于具有强非线性的强制循环蒸发系统。近期以来，非线性解耦控制方法成为一个研究热点。文献 ［7－8］采用非线性模型预测控制方法实现了对蒸发过程的解耦控制。文献 ［9］提出了一种多模型预测控制和PID控制串级的智能解耦策略。上述方法的控制规律形式复杂且计算量大。文献 ［3，10］对强制循环蒸发系统采用了基于神经网络的自适应解耦控制，主要是利用神经网络的软测量建模方法，算法复杂且精度不高。为了简化设计，文献 ［11］采用了基于反馈线性化的非线性解耦控制，然而该算法的缺点是严重依赖被控对象的精确数学模型，而且控制增益矩阵中还需要直接测量系统出料温度，实现成本和难度都较高。

自抗扰 控 制［12－14］（active disturbance rejection control，ADRC）是经过多年研究发展起来的一种控制算法，对于模型依赖度极低但控制性能优良。文献 ［15］针对多变量耦合问题提出了基于自抗扰技术的非线性动态解耦控制，然而，该算法采用非线性形式导致参数调节困难。在2003年，高志强［16］提 出 了 线 性 自 抗 扰 控 制 （linear active disturbance rejection control，LADRC），进一步简化了控制算法，规范了参数调节过程，并且在许多实际工程中得到成功的应用［17－18］。

本文对强制循环蒸发系统的线性定常自抗扰解耦控制进行了鲁棒性设计。首先利用降维扩张状态观测器的动态补偿线性化作用将液位和出料密度两个控制回路分别转化为近似积分器环节并进行比例控制。然后，将控制增益矩阵设定为未知常数阵，即为该算法的控制参数，避免了使用不易测状态。为了保证在大工况情况下解耦效果的总体优化，引入了高效的粒子群算法［19］对定常的控制增益矩阵和比例增益进行优化。最终，通过数值仿真，验证了该算法的有效性和在大工况内的强鲁棒性。

1 强制循环蒸发系统的描述

1.1 工艺过程

强制循环蒸发系统的原理如图1所示，主要由分离室、加热室、循环泵、出料阀和进汽阀组成。

图1 强制循环蒸发系统的原理图Fig.1 Schematic chart of forced－circulation evaporation system

在整个过程中，进料和具有高体积流量的循环溶液汇合后经循环泵进入由蒸汽进行加热的加热室，加热后的溶液进入分离室进行蒸汽溶液分离，被排出的蒸汽将用于其他过程的加热蒸汽；而对于溶液，一部分作为出料 （产品）被排出，另一部分则作为循环溶液再次与进料汇合。

1.2 强制循环蒸发系统的动态模型

假设系统是绝热的，没有热损失，系统中所有溶液的比热容和蒸汽的汽化潜热为常数。根据质量和能量守恒原理，文献 ［20］建立了强制循环蒸发系统的动态模型

式中，h为强制循环蒸发系统的分离室液位，m；ρ为出料密度，kg·m－3；T为出料温度，℃；QP为出料流量，m3·h－1；ms为加热蒸汽流量，kg·h－1；A为蒸发器的横截面积，m2；QF为进料流量，m3·h－1；ρW为水密度，kg·m－3；ρF为进料密度，kg·m－3；c为溶液的比热容，kJ·（kg·℃）－1；λv为二次蒸汽的汽化潜热，kJ·kg－1；cF为进料的比热容，kJ·（kg·℃）－1；TF为进料温度，℃；λs为加热蒸汽的汽化潜热，kJ·kg－1。

由动态模型 （1）可以看出，变量h和ρ的动态方程中都包含可操纵变量QP和ms，且它们之间不是简单的线性关系，即任何一个可操纵变量的变化会同时影响h和ρ，因此该控制对象是一个具有强耦合性和强非线性的复杂工业过程。

2 线性定常自抗扰解耦控制

选取如下状态变量 ［x1x2x3］＝ ［hρT］，输入变量 ［u1u2］＝ ［QPms］，输出变量 ［y1y2］＝［x1x2］，式 （1）可等效为

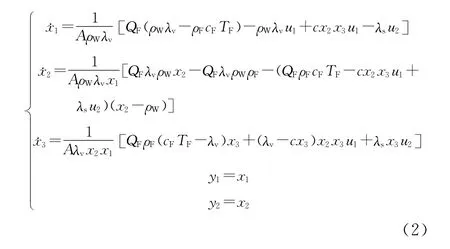
即为强制循环蒸发系统的多输入多输出状态方程。

线性定常自抗扰解耦控制的结构框图如图2所示。

图2 线性定常自抗扰解耦控制的结构框图Fig.2 Schematic diagram of linear time－invariant active disturbance rejection decoupling control

将 （2）改写为

设fi（x1，x2，x3）为 “动态耦合”，而Bi［u1u］2T为 “静态耦合”。其中

假设

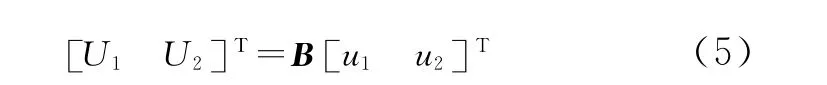
其中，U1，U2为虚拟控制量，将式 （5）代入式 （3）可得

此时，系统中的虚拟控制量U1、U2与被控输出y1、y2对应为单输入单输出关系。

下面分别针对系统液位和出料密度两个回路设计LADRC。式 （6）的每个回路可以描述为

设x1，i＝xi，x2，i＝fi（x1，x2，x3），则

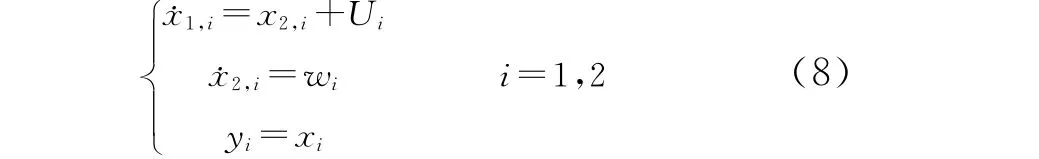
此处，wi是一个干扰信号。同时，把 “动态耦合”部分xi，2定义为扩张状态［13］，因此可以对式（8）设计全维扩张状态观测器。借鉴文献 ［16］中观测器带宽的参数化设计，在状态x1，i可以直接测量的情况下，按照文献 ［21－22］中的方法设计降维观测器如下

其中，z2，i用来估计式 （8）中扩张状态xi，2，也就是 “动态耦合”部分fi（x1，x2，x3）；ω0，i为对应降维观测器的带宽。因为˙x1，i不能通过直接测量得到，需要定义一个新变量

由式 （9）和式 （10）可以得出式 （7）的降维线性扩张状态观测器为

选取合适的观测器带宽ω0，i，可使

设计虚拟控制量为

其中，u0，i为降维扩张状态观测器对回路进行动态补偿线性化后的系统输入。将式 （13）代入式（7）并结合式 （12）可得

通过降维线性扩张状态观测器，将强制循环蒸发系统的两个回路分别线性化为虚拟控制量的积分器形式。

这里u0，i可采用经典的比例控制形式

其中，ri为参考指令信号。

由式 （5）、式 （13）和式 （15）可以得到强制循环蒸发系统的实际控制量为

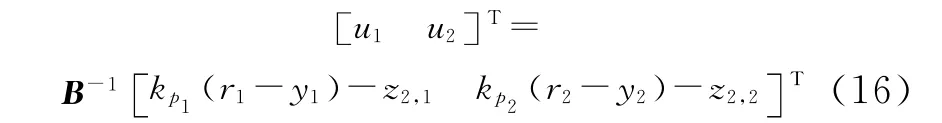
由以上分析知，应用降维扩张状态观测器，可以实时估计 “动态耦合”部分，此时，只需要计算“静态耦合”部分的B。这在一定程度上降低了控制器对精确模型的依赖程度，同时降维线性扩张状态观测器又降低了控制器的阶次，提高了系统的稳定性。

然而，矩阵B是由各个系统参数和状态变量的函数组成的，因此对于系统数学模型的依赖程度依然较高，特别是其与出料温度T具有一定相关性。如何在可能的工况范围内确定一个固定合理的B使得平均解耦控制性能近似最优，不仅可以极大降低对于实际传感测量的要求和对于精确模型的依赖，而且还可以实现线性定常控制，大幅度降低控制器的实现难度。考虑到上述问题，可以将B矩阵设置为未知常数矩阵，与比例控制器的比例增益一起作为线性定常自抗扰解耦控制器的设计参数。文献 ［23］针对超音速飞机的多控制参数优化问题，提出了一种基于遗传算法的鲁棒飞行控制设计。本文通过粒子群算法优化控制参数，保证了控制器在大工况内的解耦性能鲁棒性。

3 基于粒子群算法的控制参数优化方法

粒子群算法是一种基于群体智能的优化算法。在粒子群算法中，每个粒子i在时刻t的位置为xti，速度为vti：位置对应于优化问题的可行解，其优劣程度由事先确定的适应度函数评价；每一粒子以速度vti在该优化问题的可行域空间内飞行，最终逼近目标函数的全局最优点。

设搜索空间为D，迭代次数为M，种群规模为N。设粒子群的位置和速度为

粒子的历史最优位置可表示为＝而粒子当前时刻的全局最优位置为因此，粒子在t＋1时刻的位置更新公式为

适应度函数是判断粒子优劣程度的标准，在本文中，适应度函数用于评价闭环系统的解耦程度。为保证控制方法在系统的全工作范围内有效，本文根据均匀设计原理［25］，在运行空间内选取n个工作点；在每个工作点处基于小扰动假设进行线性化并分别求取闭环传递函数；根据对角优势定理［26］，设计适应度函数为

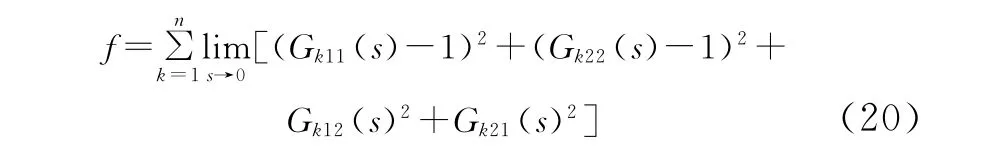
利用粒子群算法优化矩阵B、kp1和kp2的值，保证了定常控制参数可以适应整个工况范围内解耦控制性能的鲁棒性。

图3 参数动态优化曲线Fig.3 Dynamic curves of optimized parameters

4 仿真研究

为了验证本文所提的基于粒子群算法的线性定常自抗扰解耦控制方法的有效性与鲁棒性，进行了随动跟踪仿真，出料温度不确定性仿真和抗干扰仿真。

强制循环蒸发系统的模型参数为［10］：λv＝2247 kJ·kg－1，λs＝2185kJ·kg－1，QF＝80m3·h－1，ρF＝1365kg·m－3，cF＝3.61kJ·（kg·℃）－1，TF＝100℃，ρW＝1000kg·m－3，A＝40m2，c＝3.6kJ·（kg·℃）－1。强制循环蒸发系统的初始条件：x1＝2，x2＝1429.4，x3＝107.5，u1＝68，u2＝11200。

表1 均匀设计表U5（52）Table 1 Uniform design table of U5 （52）

（1）随动跟踪仿真。在数学仿真过程中，液位的设定值为r1＝2.3，在t＝8时，设定值上升为r1＝2.6；出料密度的设定值为r2＝1435，在t＝8时，设定值上升为r2＝1440，在t＝12时，又降回r2＝1435，其他边界值保持不变。在这个仿真中还与文献 ［11］提出的非线性解耦控制方法进行了比较，仿真结果如图4、图5和图6所示。由图4和图5可以看出，应用线性定常自抗扰解耦控制方法的强制循环蒸发系统的液位波动较小，出料密度也能快速地跟踪设定值，并且达到满意的解耦效果，尤其在液位回路比应用非线性解耦控制方法的效果好。图6显示了应用两种控制算法时的出料温度变化范围。

图4 液位Fig.4 Liquid level

图5 出料密度Fig.5 Product density

（2）出料温度不确定性仿真。为了验证控制器对不同出料温度初值的鲁棒性，温度初值分别在［50℃，200℃ ］范围内每隔10℃取一个点，仿真结果如图7和图8所示，验证了线性定常自抗扰解耦控制器对于系统出料温度初值变化的控制性能鲁棒性很强，即使不采用温度信息也可以保证足够的动态性能。

图6 出料温度Fig.6 Temperature of product

图7 温度初值变化对液位的影响Fig.7 Liquid level subject to initial temperature change

图8 温度初值变化对出料密度的影响Fig.8 Product density subject to initial temperature change

图9 高频随机噪声对液位的影响Fig.9 Liquid level subject to high－frequency noise

图10 高频随机噪声对出料密度的影响Fig.10 Product density subject to high－frequency noise

5 结 论

本文首先对强制循环蒸发系统动态模型进行分析，引入虚拟控制量，完成两回路单输入单输出的配置，随后进行了线性定常自抗扰解耦控制的设计。利用粒子群算法优化出控制增益矩阵和比例增益的常值，以保证定常参数依然可以在大工况范围内具有很强的解耦性能鲁棒性。数学仿真研究表明了该算法对强制循环蒸发系统具有良好的控制性能，同时对工业实际中的大工况变化和干扰，具有良好的性能鲁棒性。该算法需要的测量信息少，控制器实现简单，解耦控制鲁棒性强，对于实际应用具有参考价值。

图11 液位抗低频正弦干扰效果Fig.11 Low－frequency sinusoidal interference rejection of the liquid level

图12 出料密度抗低频正弦干扰效果Fig.12 Low－frequency sinusoidal interference rejection of product density

符 号 说 明

A——蒸发器的横截面积，m2

c，cF——分别为溶液、进料的比热容，J·kg－1·℃－1

h——分离室的液位，m

ms——加热蒸汽的流量，kg·h－1

QF，QP——分别为进料、出料的流量，m3·h－1

T，TF——分别为溶液、进料的温度，℃

λs，λv——分别为加热蒸汽、二次蒸汽的汽化潜热，J·kg－1

ρ，ρF，ρW——分别为出料、进料、水的密度，kg·m－3

下角标

F——进料

P——出料

W——水

s——加热蒸汽

v——二次蒸汽

［1］ Du Ying（杜莹），Li Yongguang（李永光）.Entropy analysis of evaporator in boiling two－phase flow region ［J］.CIESC Journal（化工学报），2011，62 （5）：1185－1190.

［2］ Wang Yonggang （王 永 刚 ），Chai Tianyou （柴 天 佑 ）.Nonlinear adaptive decoupling PID control for the forcedcirculation evaporation system ［J］.ControlTheoryAppl.（控制理论与应用），2011，28 （9）：1145－1153.

［3］ Wang Y，Chai T，Fu J，Sun J.Adaptive decoupling control of the forced－circulation evaporation system using neural networks and multiple models／／American Control Conference［C］.2011：5061－5066.

［4］ Wang J，Wang Y，Shao H.Performance improvement of VAV air conditioning control system through diagonal matrix decoupling and Lonworks technology ［J］.Energ.Buildings，2004，37 （9）：911－919.

［5］ Li Xu（李旭），Zhang Dianhua（张殿华），Zhou Na（周娜），Liu Xianghua （刘 相 华 ），Wang Guodong （王 国 栋 ）.Decoupling looper height and tension control system with characteristic locus method ［J］.Inform.andControl（信息与控制），2005，34 （6）：665－668.

［6］ Jiang Hongmei（蒋 红 梅 ），Ren Qingchang （任 庆 昌 ）.Research on adaptive decoupling control in variable air volume air conditioning system ［J］.Comput.Eng.andAppl.（计算机工程与应用），2012，48 （30）：210－215.

［7］ Rangaiah G P，Saha P，Tade M O.Nonlinear model predictive control of an industrial four－stage evaporator systemviasimulation ［J］.Chem.Eng.J.，2002，87（3）：285－299.

［8］ Shi YuJing （石 宇 静），Wang Yonggang （王 永 刚），Chai Tianyou（柴天佑）.Multiple models decoupling predictive control of forced－circulation evaporation system ［J］.SystemsEngineering－Theory＆Practice（系统工程理论与实践），2010，20 （1）：131－139.

［9］ Li Shanqiang（李善强），Shi Yujing（石宇静），Chai Tianyou（柴天佑），Chen Dongyan（陈东彦）.Intelligent decoupling control of forced－circulation evaporation system ［J］.ElectricMachinesandControl（电机与控制学报），2011，15（6）：84－90.

［10］ Wang Y，Chai T，Fu J，Sun J，Wang H.Adaptive decoupling switching control of the forced－circulation evaporation system using neural networks ［J］.IEEETrans.ControlSyst.Technol.，2013，21 （3）：964－974.

［11］ Wang Yonggang （王 永 刚），Li Haibo （李 海 波 ），Chai Tianyou（柴天佑）.Nonlinear decoupling control of forcedcirculation evaporator ［J］.CIESCJournal（化 工 学 报），2013，64 （6）：2145－2152.

［12］ Han Jingqing（韩京清）.Active disturbance rejection control and it's applications ［J］.ControlandDecision（控制与决策），1998，13 （1）：19－23.

［13］ Han J.From PID to active disturbance rejection control［J］.IEEETrans.Ind.Electron.，2009，56 （3）：900－906.

［14］ Huang Yi（黄一），Xue Wenchao （薛文超），Zhao Chunzhe（赵春哲）.Active disturbance rejection control：methodology and theoretical analysis［J］.J.Sys.Sci.＆Math.Scis.（系统科学与数学），2011，31 （9）：1111－1129.

［15］ Su Sixian （苏 思 贤），Yang Huizhong （杨 慧 中）.Active disturbance rejection dynamic nonlinear decoupling control for a class of multivariable systems ［J］.CIESCJournal（化工学报），2010，61 （8）：1949－1954.

［16］ Gao Z.Scaling and bandwidth－parameterization based controller tuning／／American Control Conference ［C］.2003：4989－4996.

［17］ Zheng Q，Goforth F J.An active disturbance rejection based control approach for hysteretic systems／／IEEE Conference on Decision and Control［C］.2010：3748－3753.

［18］ Zheng Q，Dong L，Lee D H，Gao Z.Active disturbance rejection control and implementation for MEMS gyroscope［J］.IEEETrans.ControlSyst.Technol.，2007，17 （6）：1432－1438.

［19］ Kennedy J，Eberhart R.Particle swarm optimization／／IEEE International Conference on Neural Networks ［C］.1995：1942－1948.

［20］ To L C，Tade M O，Kraetzl M，Le Page G P.Nonlinear control of a simulated industrial evaporation process［J］.J.ProcessControl，1995，5 （3）：173－182.

［21］ Wang Y，Sun M，Wang Z，Liu Z，Chen Z.A novel disturbance－observer based friction compensation scheme for ball and plate system ［J］.ISATrans.，2013，53 （2）：671－678.

［22］ Qiu D，Sun M，Wang Z，Wang Y，Chen Z.Practical winddisturbance rejection for large deep space observatory antenna［J］.IEEETrans.ControlSyst.Technol.，2014，22 （5）：1983－1990.

［23］ Marrison C L，Stengel R F.Design of robust control systems for a hypersonic aircraft ［J］.J.Guid.Control Dyn.，1998，21 （1）：58－61.

［24］ Jiao B，Lian Z，Gu X.A dynamic inertia weight particle swarm optimization algorithm ［J］.ChaosSoliton.Fract.，2008，37 （3）：698－705.

［25］ Huang Yongqing（黄永清），Liang Changyong（梁昌勇），Zhang Xiangde（张祥德）.Parameter establishment of an ant system based on uniform design ［J］.ControlandDecision（控制与决策），2006，21 （1）：93－96.

［26］ Rosenbrock H H.Design of multivariable control systems using the inverse Nyquist array／／Proceedings of the Institution of Electrical Engineers ［C］.1969：1929－1936.