竖直微肋管内LNG流动沸腾传热特性的分析

徐彬，石玉美

（上海交通大学制冷与低温工程研究所，上海200240）

引 言

作为一种清洁、高效、经济的能源，天然气（NG）被越来越广泛地应用在工业生产、运输业以及民用等各领域。为方便储运，天然气通常经过除杂、液化，以液化天然气 （LNG）的形式进行储存和输运［1］。最终使用时，液化天然气需经过气化转化为常温气体。在天然气液化以及LNG气化过程中，换热器的设计以及传热特性的研究显得尤为重要。

虽然早在20世纪60年代就已开始了两相流动沸腾的研究［2］，然而，在公开发表的文献中很难找到针对LNG的两相流动沸腾的研究报告。目前，针对强化管内两相流动沸腾研究的流动介质多为制冷剂［3］。胡 海 涛 等［4］对 R410A－油 混 合物在7mm强化管内流动沸腾的传热特性进行了研究。Kravchenko等［5］研究了甲烷在竖直管内的池沸腾传热特性。Kim等［6］研究了R22在7mm和9.52mm光管和微肋管内流动沸腾传热特性，得出在7mm和9.52mm微肋管内传热系数分别是光管内传热系数的1.2～1.8倍、2.2～3.3倍的结论。Colombo等［7］对R134A在微肋管内冷凝、蒸发的传热及压降特性进行了实验研究，并且可视化分析了微肋对流型的影响。Wellsandt等［8］基于R134A的实验数据，开发了微肋管内换热关联式，关联式平均误差为1.5%，标准差为21%。然而，目前已有的关于强化管内两相流动的研究大部分是以常温下的制冷剂作为流动工质的［9］。

本文针对竖直内螺纹管内LNG的流动沸腾，实验研究LNG在流动沸腾过程中的传热特性，分析热通量、质量流量以及入口压力对LNG两相流动传热特性的影响。针对实验工况分别采用Kim、Koyama以及两种不同Ftp系数的Wellsandt关联式对传热系数进行预测，并将实验结果与预测结果进行比较。

1 实验装置

实验系统如图1所示，主要由LNG流动管路、真空杜瓦、信号采集系统3部分组成。通过调节高压储罐自增压阀和减压阀得到所需的测试管段入口压力。调节液氮生物容器中液氮的液位高度，对管路中的LNG进行预冷。测试段出口处LNG进入汽化器实现完全汽化，并通过质量流量计测量流量后排入空气。各待测点的温度、压力以及加热直流电源的电压和电流信号均通过数据采集仪采集，质量流量信号直接通过质量流量计采集并储存在计算机中。

实验管段为竖直内螺纹圆管，紫铜材质，测试管有效加热长度为1000mm，外直径为12.7mm，翅根壁厚为0.457mm，翅高为0.254mm，翅顶角度为40°，翅片数为60，螺旋角为18°。内螺纹管外观图、剖面图以及结构示意图分别如图2（a）、（b），图3所示。测试段结构如图4、图5所示，6个测温截面在测试段上均匀布置，每个截面对称布有2个铂电阻。此外，在测试段出口位置布置1个铂电阻对出口截面的管外壁面温度进行测量，在测试段入口处设计了测温沉孔，用于测量入口LNG流体温度。如图3所示，测试管段外部均匀缠绕加电热丝，并均匀涂抹导热硅酯以使得加热均匀，有效加热长度为1m。电加热丝外部依次包裹有羊毛毡、铝箔，且整个测试段置于真空杜瓦中以减少漏热。

2 实验研究

2.1 数据测量及不确定性分析

主要测量参数为：测试管段进口压力、进出口压差、LNG流量、流动方向上7个不同截面处的管外壁面温度以及入口处流体温度，电加热丝两端的电压及电加热丝上流过的电流。

图1 实验装置系统Fig.1 System diagram of experimental apparatus

图2 内螺纹微肋管实物图Fig.2 Photography of helix micro－fin tube

图3 内螺纹微肋管结构示意图Fig.3 Schematic diagram of helix micro－fin tube’s structure

图4 测试段结构示意图Fig.4 Schematic diagram of test section

图5 测试段截面示意图Fig.5 Schematic diagram of test tube cross－section

实验管段内径、有效加热长度、温度的测量不确定度分别为±0.001mm、±0.5mm、±0.1K，压力传感器的测量不确定度均为±0.3kPa，压差传感器的测量不确定度均为±0.175kPa，质量流量计标定精度为读数的±0.8%。

实验的不确定度采用NIST［10］建议的方法进行计算。主要的实验不确定度在表1中列出。

表1 不确定性分析Table 1 Summary of uncertainty analysis

2.2 漏热分析

系统的漏热量主要包含两部分：加热管段辐射漏热和两端的轴向导热漏热。根据文献 ［11］，加热管段两端的轴向导热漏热量所占比例很小，因此只考虑辐射漏热。

D′为包扎后直径，且D′＝80mm，Tw1、Tw2分别为杜瓦壁面温度和包扎层温度，按温差最大情况取值，Tw1＝293.0K，Tw2＝110K，ε1、ε2分别为杜瓦不锈钢壁面和实验管段外层铝箔片的发射率，均取为0.1。计算得到dQ＝5.42W，按照最小加热功率Q＝200W，得到dQ／Q＝2.71%。

2.3 实验工况

实验测量了入口压力Pin＝0.3～0.9MPa，质量流量G＝24.91～99.62kg·m－2·s－1，热通量q＝5.05～25.18kW·m－2范围内的96组工况。表2列出了具体的实验工况点。

2.4 数据处理

热通量由加热丝两端的电压和电流值确定

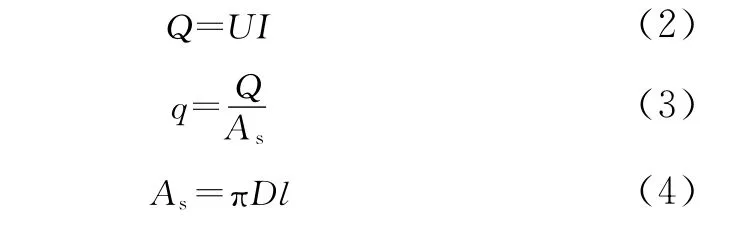
管内壁面温度可由测得的管外壁面温度，利用热传导方程进行计算得到

局部传热系数为

式中，Tf，z为z处管内主流流体温度。

各测试截面的管内LNG物性参数如Tf，z、干度、黏度、气液组分比等，综合考虑混合物相平衡以及热平衡计算得到。本文选用的相平衡方程为Peng－Robinson方程。各测试截面的压力由测得的入口压力以及实验段压差，采用线性差分计算得到。实验所用LNG的组分表由上海天然气管网有限公司提供，如表3所示。

3 实验结果与分析

3.1 热通量对传热系数的影响

如图6所示，分别比较了不同热通量对传热系数的影响。图6（a）～（d）分别给出了入口压力Pin＝0.3～0.9MPa，质量流量G＝24.91～99.62 kg·m－2·s－112组不同的工况中，当热通量不同时，各测试截面的局部传热系数随截面干度变化的曲线。可以看出，在干度较低的区域，随着热通量的增加，各测试截面的局部传热系数呈明显增大的趋势。从传热机理的角度进行分析，根据Chen［12］的经典传热理论，流动沸腾是由核态沸腾和强制对流两部分组成，在干度较小的区域内，核态沸腾占据主导地位，而核态沸腾与热通量关系密切，随着热通量的增加而增加，核态沸腾换热增强，因此局部传热系数增加。

此外，沿着液化天然气的流动方向，局部传热系数都呈现先上升而后下降的趋势。这是由于在靠近入口的加热起始阶段，管内天然气的截面干度较低，两相流动沸腾中核态沸腾占主导地位，对总的换热效果影响较大。随着加热的进行，管内天然气不断被气化，截面干度逐渐增加，流动逐渐由核态沸腾主导区域向强制对流换热主导区域进行转变，换热效果增强，总的传热系数增加。而当加热继续，管内天然气干度达到较高的值，此时管段内天然气气体比例较高，液相组分很容易脱离加热管段内壁面，传热出现恶化，局部传热系数明显下降。

表2 实验工况点Table 2 Experimental conditions list

表3 LNG组分Table 3 Composition of LNG／% （mol）

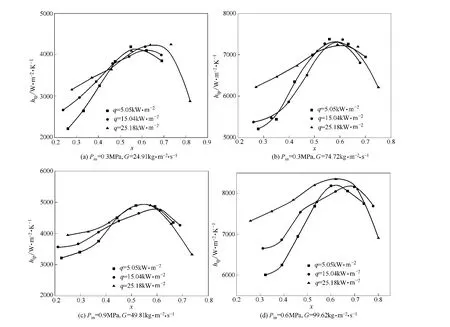
图6 热通量对传热系数的影响Fig.6 Effect of heat flux on heat transfer coefficient

3.2 质量流量对传热系数的影响

图7（a）～（f）分别给出了当入口压力Pin＝0.3、0.6、0.9MPa，而热通量q＝15.04W·m－2和q＝25.18W·m－2时，不同质量流量下的局部传热系数随截面干度的变化曲线。结果表明，局部传热系数随质量流量的变化很明显，随着质量流量的增加，传热系数明显增大。原因分析：根据经典传热理论，在干度较大的区域，强制对流传热在整个流动沸腾传热中占主导地位，而强制对流传热系数是被加热工质流动速度的正相关函数，随着质量流量的增加，流速增加，强制对流传热效果增强，总的传热系数增加。较高的质量流量能够增强管内流动的湍流效应，这将有助于增加管内流体的不均匀性，使得气液两相之间的相互作用增强，从而最终也将使得流动沸腾的换热效果增强，传热系数增大。

3.3 入口压力对传热系数的影响

图8比较了不同入口压力时，流动沸腾传热系数沿着截面干度的变化情况。可以看出，在相同的干度范围内，随着入口压力的增加，传热系数呈现下降的趋势。出现这一现象的原因可能是过高的入口压力抑制了LNG在流动沸腾过程气泡的生成，从而减弱了沸腾的强度，导致换热性能降低，传热系数下降。相应地，当入口压力较低时，气泡更容易形成和生长，从而有效地强化了沸腾换热效果，使得局部传热系数增加。

4 与已有关联式的比较

4.1 微肋管管内流动沸腾换热关联式

以往研究中，强化管内流动沸腾的流动工质多为制冷剂等常规工质。表4为本文所采用关联式的具体形式。

Kim关联式中的系数C1～C9如表5所示。

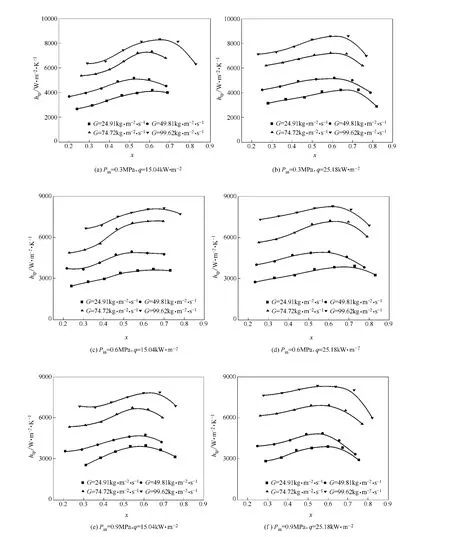
图7 质量流量对沸腾传热系数的影响Fig.7 Effect of mass flow rate on heat transfer coefficient

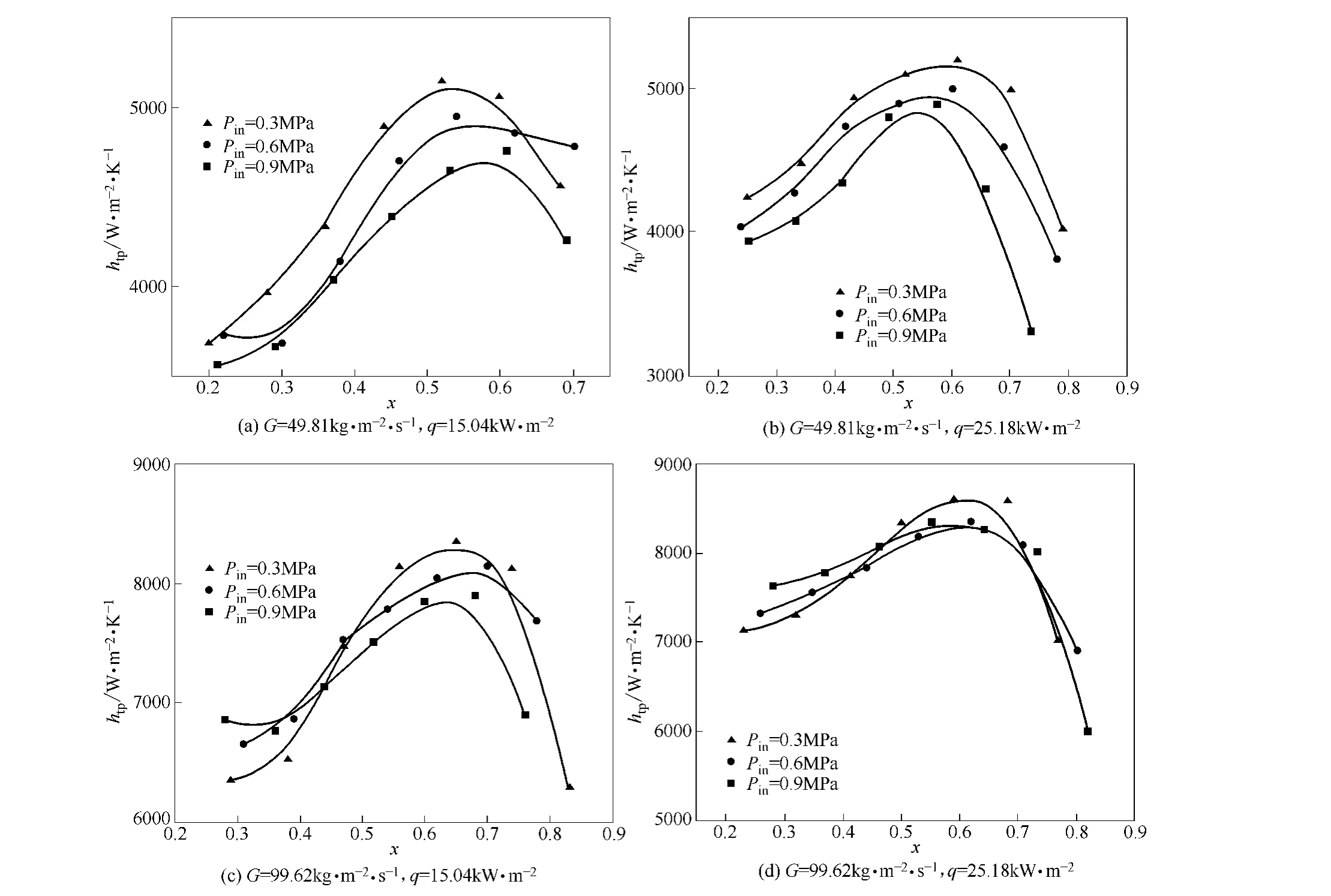
图8 入口压力对沸腾传热系数的影响Fig.8 Effect of inlet pressure on heat transfer coefficient

表4 流动沸腾传热系数关联式Table 4 Flow boiling heat transfer correlation used in this paper

Continued

表5 Kim关联式中C1～C9系数Table 5 C1—C9in Kim’s correlation

4.2 换热关联式预测结果与实验数据的比较

如图9所示，将质量流量为24.9～112.1kg·m－2·s－1，热通量为5.1～25.1kW·m－2和入口压力为0.37～1.02MPa的224个实验数据点分别与上述3种关联式的预测值进行了比较。

表6列出了实验工况范围内4个不同关联式的预测值与实验值之间的偏差情况，其中包括平均绝对误差和标准误差。比较发现，在整个实验工况范围内，Koyama关联式的准确性最好，平均绝对误差和标准误差均最小，分别为38.7%和25.6%。

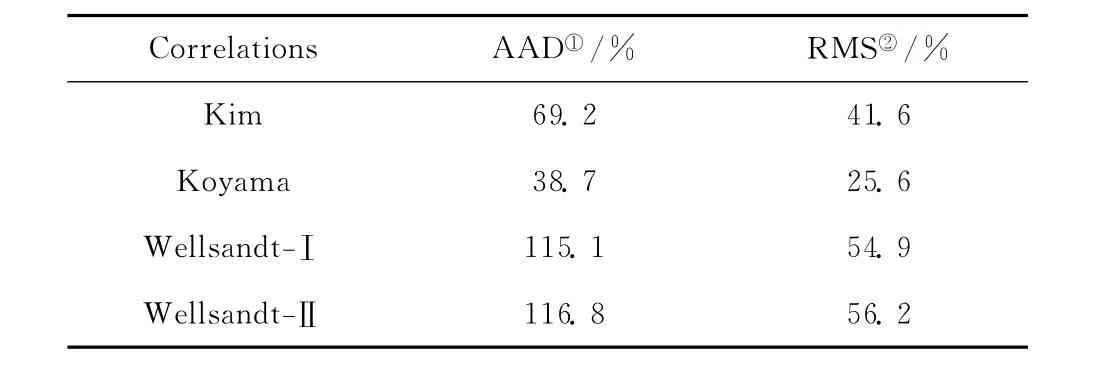
表6 各关联式预测结果与实验值之间的偏差Table 6 Deviation between predicted HTC and experimental data

5 结 论

（1）分析热通量、质量流量以及入口压力对液氮两相流动传热特性的影响。实验结果表明，在干度较小的区域，随着热通量的增加，传热系数增大，换热效果明显增强；沿着液化天然气的流动方向，局部传热系数都呈现先上升而后下降的趋势。局部传热系数随质量流量的变化很明显，随着质量流量的增加，传热系数明显增大。随着入口压力的增加，传热系数减小，分析认为此时入口压力的增加抑制了气泡的生成，从而使换热效果减弱。

（2）采用4种微翅管内流动沸腾换热关联式，即Kim、Koyama以及两种不同Ftp系数的Wellsandt关联式分别对实验工况下的传热系数进行预测，并与实验结果比较。结果表明，在实验工况范围内，Koyama关联式准确性最好。

符 号 说 明

Ac，As——分别为流道截面积、流道有效受热面积，m2

Di，Do——分别为实验管段内径、外径，m

G——质量流量，kg·s－1

h——局部传热系数

hi，ho——分别为入口焓、出口焓，J·kg－1

hlv——汽化潜热，J·kg－1

I——电流，A

l，lsc——分别为实验段长度、过冷段长度，m

M——分子量

图9 实验数据与4种常用关联式的比较Fig.9 Experimental data compared with 4commonly used correlations

P——压力，Pa

Pr——Prandtl数

Q——加热量，W

q——热通量，W·m－2

Re——Reynolds数

T——热力学温度，K

U——电压，V

Xtt——Martinelli参数

x——干度

z——坐标

λ——热导率，W·m－1·K－1

μ——动力黏度，Pa·s－1

ρ——密度，kg·m－3

下角标

f——管内流体

in——实验段入口

out——实验段出口

sat——饱和状态

TP——两相

w——壁面

［1］ Gu Anzhong （顾安忠）.LNG Technical Manual（液化天然气技术手册）［M］.Beijing：China Machine Press，2010：1－5.

［2］ Chen J C.Correlation for boiling heat transfer to saturated fluids in convective flow ［J］.IndustrialJournalofHeatand MassTransfer，1986，3：351－358.

［3］ Zou Xin （邹鑫），Gong Maoqiong （公 茂 琼）.Review on flow boiling heat transfer correlations of cryogenic fluids ［J］.JournalofRefrigeration（制冷学报），2008，29 （2）：1－7.

［4］ Hu Haitao（胡海涛），Ding Guoliang （丁国良），Wang Kaijian （王 凯 建 ）.Heat transfer characteristics of flow boiling of R410A－oil mixture in a 7mm enhanced tube ［J］.JournalofChemicalIndustryandEngineering（China）（化工学报），2008，59 （1）：32－37.

［5］ Kravchenko V A，Tolubinskaya L F，Pyatnichko A I.Heat transfer in boiling of methane at equals 1.02bar ［J］.Heat TransferSov.Res.，1975，7 （3）：27－30.

［6］ Seo K，Kim Y.Evaporation heat transfer and pressure drop of R－22in 7and 9.52mm smooth／micro－fin tubes ［J］.InternationalJournalofHeatandMassTransfer，2000，40：2869－2882.

［7］ Colombo L P M，Lucchini A，Muzzio A.Flow patterns，heat transfer and pressure drop for evaporation and condensation of R134Ain microfin tubes ［J］.InternationalJournal ofRefrigeration，2012，35：2150－2165.

［8］ Wellsandt S，Vamling L.Prediction method for flow boiling heat transfer in a herringbone microfin tube ［J］.InternationalJournalofRefrigeration，2005，28：912－920.

［9］ Miyara A，Otsubo Y，Ohtsuka S.Evaporation heat transfer of R410Ain herringbone micro fin tubes／／Proceedings of the Conference of the International Institute of Refrigeration Commission B1 ［C ］ .Paderborn，Germany，2001.

［10］ Taylor B N，Kuyatt C E.Guidelines for evaluating and expressing the uncertainty of NIST measurement results，national institute of standards and technology ［J］.TechnicalNote，1994：1297.

［11］ Qi Shouliang （齐 守 良）.Flow and heat transfer of liquid nitrogen in micro－tubes ［D］.Shanghai：Shanghai Jiao Tong University，2007.

［12］ Chen J C.Correlation for boiling heat transfer to saturated fluids in convective flow ［J］.I＆ECProcessDesignand Development，1966，5 （3）：322－329.

［13］ Koyama S，Yu J，Momoki S，Fujii T，Honda H.Forced convective flow boiling heat transfer of pure refrigerants inside a horizontal microfin tube／／Proceedings of the Convective Flow Boiling Conference ［C］.1995：137－142.