解答分式相关赛题的基本策略分析

刘清泉 (镇海蛟川书院 浙江宁波 315201)



解答分式相关赛题的基本策略分析

刘清泉 (镇海蛟川书院 浙江宁波 315201)

分式是初中数学的一个重要内容，虽然分式的性质和运算与分数相似，但分式远比分数复杂．竞赛中与分式化简、求值、证明、变形和方程等相关的试题，求解时通常技巧性很强，常常要根据分式的具体特征灵活变形，以使问题得到迅速准确的解答，其中有很多方法具有典型性和代表性.笔者结合近几年各级、各类竞赛中的热点试题，归纳其中使用频率较高的技巧和方法，并梳理其中的常用策略．

1 约分先行

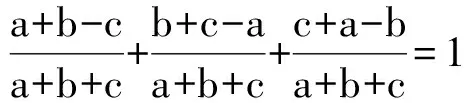
评注 约分先行，使得分式更加简约，从而利于化简.在面对较为复杂的分式问题时，通常先考虑是否可以约分．

2 分步通分

(2004年“希望杯”邀请赛初二第1试试题)

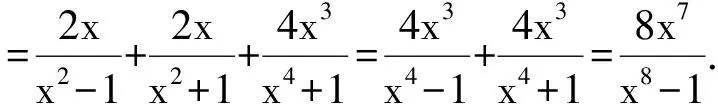
评注 相比“将原式中的4个分式一次性通分”而言，“分步通分”能更加简约地完成解答．

3 分组通分

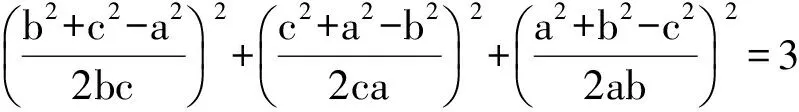
(2013年全国初中数学联赛试题)

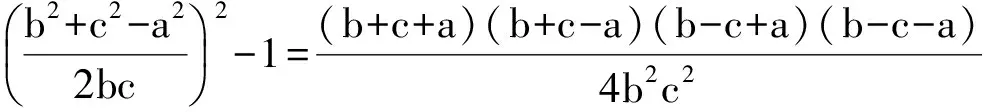
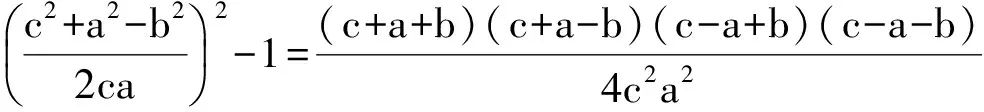
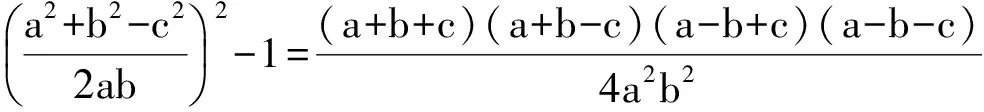
于是

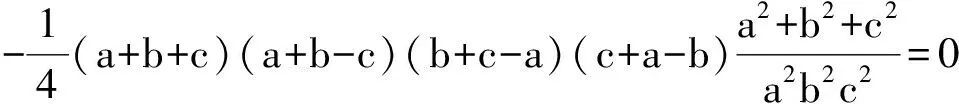
从而a+b-c=0,或b+c-a=0，或c+a-b=0.不难确定所求式的值为3.

评注 本例的解答与2007年北京市初二数学竞赛的第3大题相似，通过恰当地“分组通分”后，借助因式分解获得关键点“a+b-c=0,或b+c-a=0，或c+a-b=0”，进而求值.另外，“分组通分”在求解分式方程时也常常用到.

4 分组求和

( )

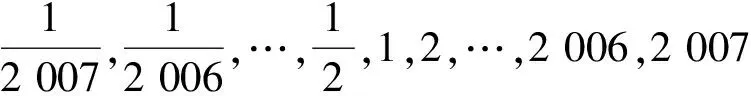
A．-1 B．1 C．0 D．2 007

(2007年全国初中数学联赛试题)

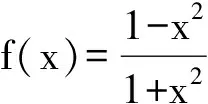
5 去掉分母

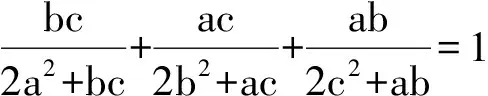
(2014年全国初中数学联赛初二试题)

解 去分母并整理，得

2a4bc+2ab4c+2abc4-6a2b2c2=0，

于是

abc(a3+b3+c3-3abc)=0，

从而

a3+b3+c3-3abc=0,

进而

(a+b+c)(a2+b2+c2-ab-bc-ca)=0,

即

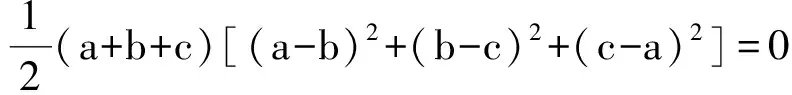
故

a+b+c=0．

评注 之所以把“去掉分母”作为一种重要的策略来阐述，是因为选择“去掉分母”求解本例略显“暴力”.面对一道压轴赛题，通常侧重技巧方法.不过，采用“去分母”的方法解答本例不失为一个好的策略．下文中会涉及解答本例的另一种方法．

6 同取倒数

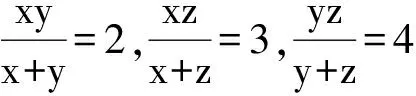
(2009年天津市数学竞赛试题)

从而

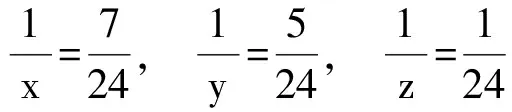
进而

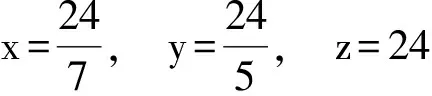
于是所求式的值为0．

评注 先“同取倒数”，后“裂项”，将问题转化为较为常见的情形，进而求解．

7 等比设“k”

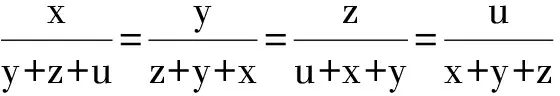
(2008年北京市初二数学竞赛试题)

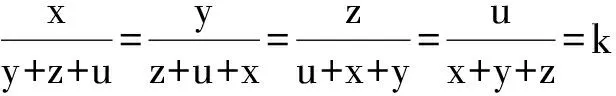
k(y+z+u)=x，k(z+u+z)=y，k(u+x+y)=z，k(x+y+z)=u,

从而

3k(x+y+z+u)=x+y+z+u,

进而

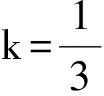
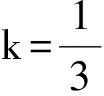
评注 本题亦可利用等比的性质求解，不过同样需要分类讨论(分2种情形：x+y+z+u=0和x+y+z+u≠0)．

8 分离整式

例8 设整数a使得关于x的一元二次方程5x2-5ax+26a-143=0的2个根都是整数，则a的值是______．

(2008年浙江省初中数学竞赛试题)

解 视a为主元，原方程可化为(5x-26)a=5x2-143，于是

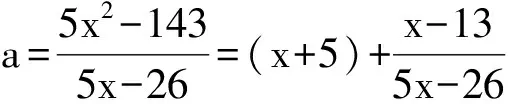
评注 本例通过“转换主元”，将关于x的二次方程转化为关于a的一次方程，在用含x的分式表示a的前提下，利用分离整式的方法确定整数x以及整数a的值．

9 裂项相消

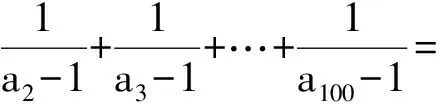
(2007年全国初中数学竞赛试题)

解 由a1+a2+…+an=n3及a1+a2+…+an-1=(n-1)3，得

an=n3-(n-1)3=3n2-3n+1,

从而

故

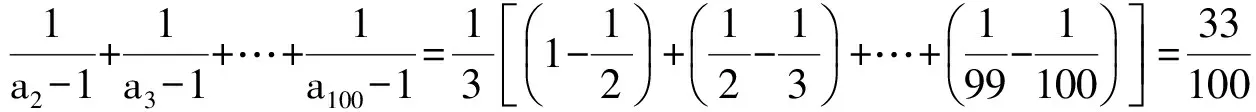
评注 分式裂项，特别是裂项相消是解答分式相关问题的常用方法，尤其是面对项数较多的问题可以优先考虑．

10 整体求值

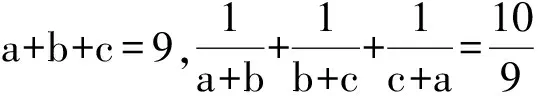
(2012年全国初中数学竞赛试题)

解 由已知可得

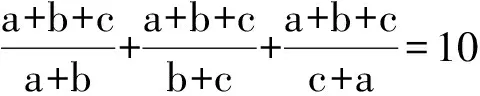
从而

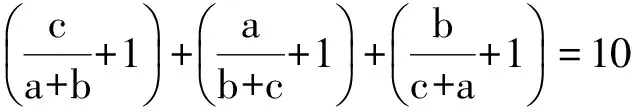
故

评注 注意到条件和结论中的分式的分母具有一致性，考虑通过适当变形整体求值．

11 整体换元

例11 利用“整体换元”解答例5.

解 由已知可得

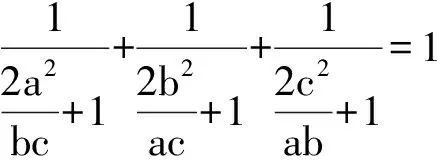
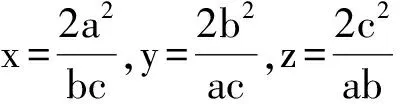
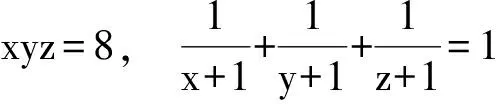
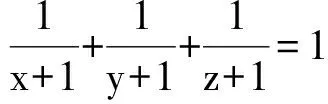
xyz=x+y+z+2，

于是

x+y+z=6，

即

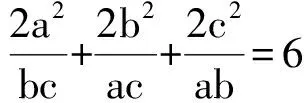
于是

a3+b3+c3-3abc=0，

从而

(a+b+c)[(a-b)2+(b-c)2+(c-a)2]=0(其中a,b,c不全相等)，

进而

a+b+c=0．

评注 换元法在求解分式方程时使用较多.值得注意的是：与整式相关问题使用换元法不同，分式相关问题使用换元法，不是题目中简单地“重复”出现了某个“部分”，而是为了化简或求值的便利，引入不同的对象，表达不同的部分．

12 整体代入

(2006年江苏省初二数学竞赛试题)

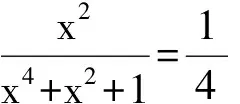
评注 解答本例方法众多，整体代入相对容易操作．

13 逆向代入

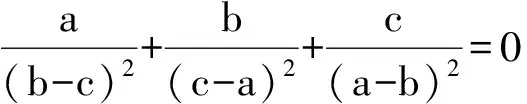
(2015年全国初中数学联赛初二试题)

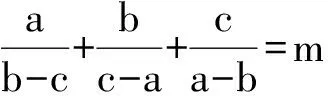
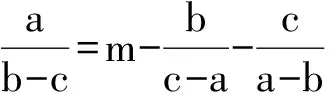
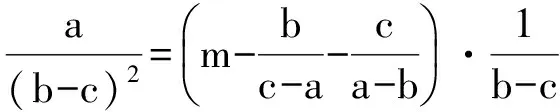
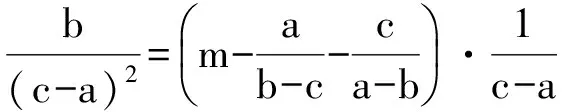
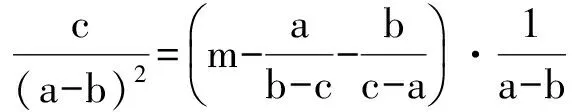
上述3个式子相加，得

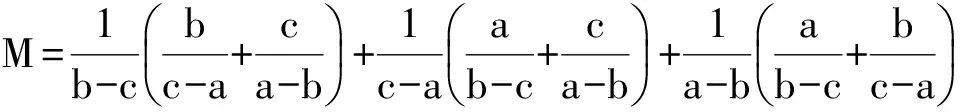
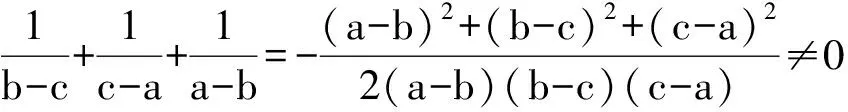
故

14 因式分解

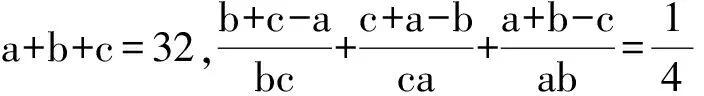
(2009年全国初中数学联赛试题)

证明 将已知条件中的2个式子相乘，得

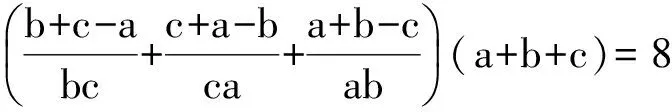
即

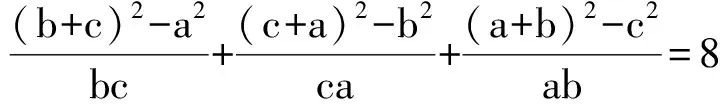
于是

a[(b+c)2-a2]+b[(c+a)2-b2]+c[(a+b)2-c2]=8abc.

展开、整理并视a为主元降幂排列，得

a3-(b+c)a2-(b-c)2a+(b+c)(b-c)2=0,

从而

a[a2-(b-c)2]-(b+c)[a2-(b-c)2]=0，

进而

(a-b-c)(a+b-c)(a-b+c)=0，

评注 表面上看题目呈现的条件是分式，但由于是与分式相关的等式问题，去分母后解题主要围绕因式分解展开，去分母并整理的等式左边是一个较为复杂的三元三次多项式，故选取主元，以主元分组因式分解，进而获得结论．当然，还可利用“轮换对称式”的性质分解因式，另外解答本题方法众多，大多以因式分解为核心环节，此处不再赘述.

15 “对勾函数”

(2015年全国初中数学联赛初三试题)

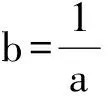
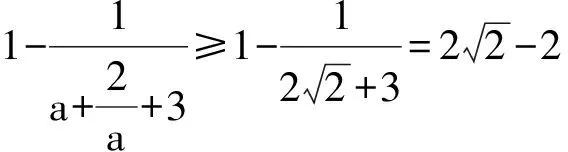
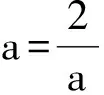
评注 “对勾函数”是初、高中数学的一个衔接内容，在近几年各级、各类竞赛试题中多有出现,常在解答代数最值或利用代数方法解答几何最值时遇到，除利用一元二次方程的判别式求解外，利用均值不等式确定最值也是不错的方法．

好问题如同蘑菇，正如波利亚在《怎样解题》中指出：“当你找到第一个蘑菇或做出第一个发现后，再四处看看，它们总是成群生长．”应该说与分式相关的问题大多比较灵活，很多时候，对同一个问题的解答方法有很多，鉴于笔者能力所限，未能将其全部归纳.另外，鉴于篇幅所限，涉及“部分分式”、“分式方程”、“增根相关”等一些问题在此不再赘述．