一种动态参数更新的无人机三维路径规划方法

张 华 史思总 周一廷 霍建文

(西南科技大学信息工程学院，四川 绵阳 621010)

一种动态参数更新的无人机三维路径规划方法

张 华 史思总 周一廷 霍建文

(西南科技大学信息工程学院，四川 绵阳 621010)

针对动态环境下无人机三维路径规划的复杂性及优化效率问题，提出了一种可视域下动态参数更新的无人机三维路径规划方法。在动态参数更新过程中，采用启发式动态更新机制的信息素进行全局更新；利用模拟栅格法进行两次空间区域划分，形成局部节点集合和全局离散点集合。先在节点集合中搜索局部路径，然后在离散点集合中搜索出最优路径。为更好地逼近真实环境，算法引入函数DF1产生复杂的三维动态环境。实验结果表明，新的蚁群算法具有较好的可行性和实时性，能够有效解决空间复杂度、搜索效率等问题，加快全局收敛速度，保持基本蚁群算法较强的鲁棒性，实时避开障碍物规划出最优路径。

无人机 三维路径规划 蚁群算法 可视域 动态参数更新

0 引言

路径规划是无人机实现自动导航的重要组成部分，但在动态环境中对无人机路径规划评价标准与静态不同，预先确定的代价函数不能反映特定任务的要求。动态环境下需要根据环境的变化实时做出反应。

王维平等在无人机轨迹规划方法的文献综述中，对规划空间的构造方法、路径规划算法进行了分类比较，同时提出分析求解无人机路径规划的过程模型[1]。Hao Meng等将遗传模拟退火算法用于无人机的三维路线规划，利用飞行路段和障碍之间的距离转换成俯仰值，并将该值添加到适应度函数，达到路径最优化的目的[2]。Liu Xin等提出利用网格和迭代惩罚方法来实现无人机多路径规划的方法，该方法自动根据高分辨率的分布地形找到最优路径，以满足无人机的可操作性的要求[3]。Zhao Junwei等提出改进变步长的A*寻优搜索算法，降低了时间和空间的计算复杂度，达到最佳的搜索策略的合理性和轨迹，从时间协调与空间协调实现多无人机空中对地攻击的路线规划[4]。洪晔等为解决算法时空开销大、无人机(unmanned aerial vehicle， UAV)航向改变频繁的缺点，提出一种基于状态聚类方法的分层马尔可夫决策过程(hierarchical Markov decision processes， HMDP)模型，并将其拓展到三维规划中，有效解决UAV 的三维全局路径规划问题，为其在实际飞行中的局部规划奠定了基础[5]。李霞等提出一种改进遗传算法的三维路径规划方法，该方法对地形高程数据进行综合平滑处理, 建立满足无人飞行器机动性能的安全飞行曲面, 结合威胁的量化模型, 采用改进遗传算法在安全飞行曲面上规划出三维飞行路径[6]。张航等提出一种量子行为粒子群优化算法的飞行器三维路径规划策略，该策略建立新地图和粒子适应度函数,从而决定静态和动态避障的适应值，可在动态和静态的环境中产生最优路径[7]。

目前，国内外对蚁群算法在动态环境下的无人机三维路径规划研究较少，同时传统蚁群算法存在收敛速度慢和易陷入局部最优的缺点。本文提出一种可视域下动态参数更新的蚁群算法，进行无人机的三维路径规划。

1 动态环境下的三维空间模型建立

设无人机初始位置为O点，目的地设为S点，视无人机模型为质点，建立无人机飞行三维坐标系O-XYZ，其中X、Y、Z轴分别与地球坐标系的三个轴平行，即初始位置O的坐标相对地球坐标的原点平移N个单位，则S点的坐标为(x,y,z)。设S点在XOZ、XOY、YOZ平面投影的点为Sxz、Sxy、Syz。由此，点Sxz、Sxy、Syz与S点坐标(x,y,z)分解的点Sx、Sy、Sz及初始点O构成三维路径规划空间，如图1所示。

图1 三维路径规划空间

在图1中，将三维空间O-S沿边OSx进行m等分，沿边OSy进行n等分，沿边OSz进行h等分，则三维空间可离散化为序号坐标(i,j,k) (i=0,1,2,…,m；j=0,1,2,…,n；k=0,1,2,…,h)和位置坐标(x,y,z)构成的三维离散点集合，则任意一点的坐标可由如下公式求得：

(1)

在三维空间中，假设O点与S点间有B1，…，Bi个简化的锥体动态障碍物。动态障碍物的模拟采用函数DF1(Dynamic Function 1)的动态模型，可模拟复杂的高维系统[8]。DF1动态模型中一个锥体的中心高度和中心位置不变化，而另外一个锥体的中心高度H和中心位置(Xd,Yd)时刻变化，从而由式(2)模拟出动态障碍物。

(2)

式中：Ri为第i个锥体的倾斜度，从而避免锥体高度之间的相互影响；(Xi,Yi)为第i个锥体的中心位置；f(Xd,Yd)为在 (Xd,Yd) 位置的适应值。

动态障碍物通过中心位置坐标、高度、倾斜度可得到局部点的坐标，从而对整个O-S三维空间进行规划，构成序号坐标和位置坐标的三维点集合空间。利用蚁群算法在三维点集合中进行规划，最终得到最优路径。

2 混合启发式蚁群算法

2.1 信息素的表示与更新

蚁群算法采用信息素来吸引蚂蚁搜索，因此信息素的设定与更新对最优路径的搜索至关重要。三维空间中构造图的节点多，若把相邻节点间的路径作为信息素的载体，算法的空间复杂度将急剧增大。为避免增大算法的空间复杂度，将|OSx|、|OSy|、|OSz|中最小的边作为空间规划等分基础，将三维空间O-S等分成M个子空间，其中M= min{|OSx|,|OSy|,|OSz|}。每个子空间都包含环境模型的三维离散点的信息素，即三维空间O-S中的每个离散点都有一个信息素值，该子空间总体的信息素构成初节点模型的信息素。

当蚂蚁位于某离散点时，对于下一点的搜索就存在一个可视区域，如图2所示，从而简化了子空间的搜索，提升了算法的搜索效率。

当蚂蚁每次到达初节点后，将根据离散点的信息素进行可视化的搜索。假设蚂蚁在子空间搜索过程中，只有前、横、纵三种运动方式，即规定蚂蚁在向前运动单位长度的情况下，运动的最大横向距离为Ly，运动的最大纵向距离为Lz。

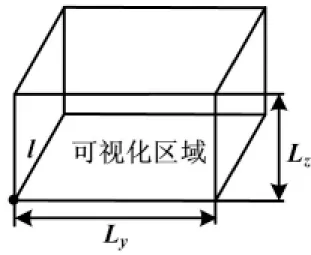
图2 蚂蚁搜索可视区域

当蚂蚁经过初节点和子空间离散点后，经过路径的信息素会进行更新处理，避免残留信息素淹没启发信息。根据上述信息素的表示，节点空间采用局部更新的方式，则蚂蚁经过节点后，该节点信息素减弱。信息素在传统算法模型[9]上，引入动态更新机制，则更新公式为：

τi′j′k′(t)=(1-ξ)τi′j′k′(t-1)+ξτ0(t0)

(3)

式中：τi′j′k′(t)为当前时刻节点的信息素，即更新后的信息素；τi′j′k′(t-1)为前一时刻节点的信息素；i′j′k′为节点的序号坐标；ξ为信息素的衰减系数，ξ∈[0,1]；τ0(t0)为节点上信息素的初值，并规定初始节点信息素与邻域产生的路径和约束条件的特征节点数成反比。

(4)

式中：τijk(t,tn)为更新后离散点的信息素值；ρ(t,tn)为信息素更新系数；τijk(t)为t时刻离散点的信息素值；i、j、k为离散点的序号坐标；Δτijk(t,tn)为在当前迭代过程中，良好个体从t时刻到tn时刻从一离散点转移到另一离散点留下的信息素量；K为系数；length(m)为第m只蚂蚁经过的路径；min表示最小值。

在搜索过程中，ρ的改变会引起算法的全局搜索能力、收敛速度的改变。为防止搜索能力下降、收敛速度减慢，ρ的值将采用自适应调节策略。设计采用挥发约束系数ω(ω∈[0,1])来约束ρ的变化，则约束公式如下[10]：

(5)

ω的过程函数关系式如下：

ω(Ni)=ω0(1-Ni/NiSum)

(6)

式中：ω0为ω的初始值；Ni为搜索次数；NiSum为总的搜索次数。

2.2 启发式函数设计

信息素大小代表对蚂蚁的初次吸引程度，蚂蚁经过后将自动更新节点信息素，而蚂蚁在可视区域从当前离散点移动到下一个离散点时，需要根据启发函数来计数区域内各离散点的选择概率。在动态环境下，路径最短和无人机的安全系数是路径规划的优化标准。路径最短包括当前离散点a与下个离散点b之间的路径最短Ld，下个离散点b与目标点S的路径最短Ls，则最短路径计算公式如下：

(7)

(8)

无人机的安全系数要求无人机尽可能地远离动态环境中的障碍物。考虑障碍物存在一定的速度，只要障碍物在空间中的模型不改变，也就是障碍物的离散点不变，则根据可视区域来考虑边界约束，其约束关系式如下：

δ=(fp-nfp)/fp

(9)

式中：fp为可视区域中点(i,j,k)中可视点的数量；nfp为可视点中不可到达区域的点的数量。

综上，启发式函数如下：

(10)

式中：α1、α2、α3为系数，表示各因素的权重。

由此，选择概率pa,b为：

(11)

2.3 路径规划策略

在动态环境下，利用蚁群算法进行无人机三维路径规划的算法流程可归纳如下。

① 根据文中所述方法，建立抽象三维空间、动态障碍物模型，设置起点和目标点位置，确定模型中所有离散点、节点、障碍物的集合，从而确定可视区域内可行点集合；设置算法运行的初始参数，将蚂蚁置于起点位置，确定蚂蚁移动方向。

② 初始化信息素值，计算出节点信息素值；依据启发函数(式10)依次计算当前离散点的可视区域内可行点集合的启发信息值。

③ 根据节点信息素值，设置蚂蚁选择在节点上运动的选择概率，节点选择概率的大小与节点信息素值成正比；按局部信息素更新方式(式3)，进行局部信息素更新。

④ 蚂蚁是否在节点中完成一次路径的搜索，若是，进入④；否，转到③。

⑤ 根据离散点选择概率函数(式11)，计算离散点的选择概率；根据各个离散点的选择概率采用赌轮盘法选择可行区域内的点。

⑥ 按全局信息素更新方式(式4)，进行全局信息素更新；在节点路径下进行搜索，并判断算法是否达到迭代次数；是，输出结果；否，转到③。

3 仿真与结果分析

3.1 实验仿真

为了验证算法的可行性，实验采用Matlab R2010a软件进行算法仿真验证。首先，按照DF1模型设置动态环境参数，地图有效区域设置为100 km×100 km×1.8 km，DF1模型中规定锥体的中心高度和位置分布为910 m、25 km、25 km，动态变化次数为1 200次。

设置路径规划起点坐标和目标点坐标分别为(2,60,0.35)、(100,4,1.5)，蚁群种群的个数为20，迭代次数为200次，蚂蚁横向、纵向的最大变动为0.2 km，信息素的衰减系数为0.9，系数K=2，ω的初始值为0.7，启发函数中的因素权重α1、α2、α3都为1。为了更好地验证算法，在仿真过程中对适应度变化进行监测，显示个体适应度值，其个体适应度值为长度加上高度，减少程序的计算量，其仿真结果如图3～图5所示。

图3 t1时刻的仿真结果图

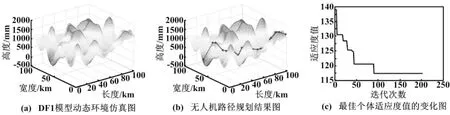
图4 t2时刻的仿真结果图

图5 t3时刻的仿真结果图

3.2 结果分析

比较分析图3(a)、4(a)、5(a)，障碍物在设定的整个空间中变化，能有效模拟现实环境，但局部锥体受到其他锥体高度的影响，锥体的变化不明显。分析图3(b)、4(b)、5(b)，路径规划的结果较为优越。比较分析图3(c)、4(c)、5(c)，随着环境障碍物的改变，达到稳定的最佳个体适应度值，需要迭代的次数不同，与环境模型的难易度有关。图6为改进的蚁群算法与蚁群算法在GPU加速情况下运行10次的时间对比图。从图6可以看出，改进的蚁群算法在实时性优于传统方法。

图7为动态环境高度值变化规律，随着动态变化次数的增加，锥体中心高度值不断变化，最后在某个值区域平稳。从图7可看出，DF1模型产生的动态环境并不是随机变化的。

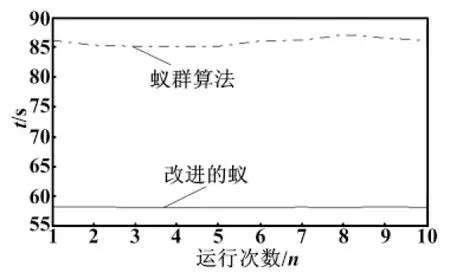
图6 改进算法与原始算法运行时间对比

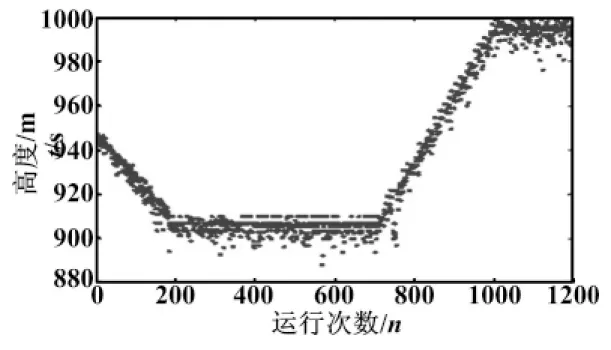
图7 动态环境高度值变化规律

仿真结果表明，算法具有可行性、可靠性。其算法的本质是基于图论的蚁群算法，根据Gutjahr W J给出的图搜索算法收敛证明[11]，算法能保证收敛，在此不再赘述。

4 结束语

针对无人机在三维空间动态环境下实时路径规划的复杂性，提出了一种可视域下动态更新参数的蚁群算法。算法引入DF1产生复杂的三维动态环境，模拟栅格法进行两次空间区域划分，形成离散点集合和节点集合。先采用节点局部搜索一次路径，然后在可视区域下离散点全局搜索，并结合自适应算法进行动态更新机制的信息素全局更新，有效解决无人机在动态环境下进行三维路径规划的空间复杂度、搜索效率等问题，提高实时性。

在实现过程中，算法需要模拟网格进行划分，如果网格划分过大，会导致路径规划达不到最优化；如果网格划分过小，则增大算法的计算量。此外，DF1产生复杂的三维动态环境，需要依赖于锥体倾斜度的约束。如何解决这些问题，有待进一步研究。

[1] 王维平,刘娟. 无人飞行器航迹规划方法综述[J].飞行力学,2010,28(2):6-10.

[2] Meng H,Xin G Z.UAV route planning based on the genetic simulated annealing algorithm[C]//Proceedings of the 2010International Conference on Mechatronics and Automation, Xi’an :IEEE,2010:788-793.

[3] Liu X,Zhou C P,Ding M Y.3D Multipath planning for UAV based on network graph[J]. Journal of Systems Engineering and Electronics,2011,22(4): 640-646.

[4] Zhao J W,Zhao J J. Path planning of multi-UAVs concealment attack based on new A* method[A]. Proceedings of the 2014 6th International Conference on Intelligent Human-Machine Systems and Cybernetics[C]//Hangzhou:IEEE,2014:401-404.

[5] 洪晔,房建成. 基于HMDP的无人机三维路径规划[J].北京航空航天大学学报,2009,35(1):100-103.

[6] 李霞,魏瑞轩,周军,等. 基于改进遗传算法的无人飞行器三维路径规划[J].西北工业大学学报，2010,28(3):343-347.

[7] 张航,刘梓溪.基于量子行为粒子群算法的微型飞行器三维路径规划[J].中南大学学报：自然科学版,2013,44(S2):58-62.

[8] Morrison R W, De J K A. A test problem generator for non-stationary environments[C]//Proceedings of the 1999 Congress on Evolutionary Computation,Washington:IEEE,1999:2047- 2053.

[9] Colorni A，Dorigo M,Maniezzo V.Ant system:optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,1996,26(1):1-13.

[10] 王慕抽.基于混合蚁群算法的物流配送路径优化研究[J].物流科技, 2013(4):50-52.

[11] Gutjahr W J.A graph-based ant system and its convergence[J].future generation computer system, 2000 (16):837-888.

A Kind of UAV Three-dimensional Path Planning Method by Dynamic Parameter Update

Aiming at the complexity and optimize efficiency problems of three-dimensional path planning of UAV(unmanned aerial vehicle) in dynamic environment, an ant colony algorithm by dynamic parameters update under a visual domain is proposed. Dynamic parameter update process of the ant algorithm, using heuristic dynamic update mechanism updates global pheromone and using the simulation grid method to zone the space twice and form the local node-set and global collection of discrete points. The algorithm searches partial path between the nodes,and then search for the optimal path between the discrete points. To better approximate real-world environment, the algorithm introduced dynamic function 1 ( DF1 ) produce complex three-dimensional dynamic environment. Through experimental results, the proposed algorithm has good feasibility and real-time for avoiding obstacle and planning the optimal path in real-time,and it can effectively solve spatial complexity, the search efficiency, and accelerate the global convergence speed at the same time maintaining the strong robustness of basic ant colony algorithm.

UAV 3D path planning Ant colony algorithm Visible region Dynamic parameter update

四川省科技厅科技支撑计划基金资助项目(编号：2014RZ0049)。

张华(1969-)，男，2006年毕业于重庆大学控制理论与控制工程专业，获博士学位，教授；主要从事机器人技术及其应用、嵌入式系统及其应用以及智能控制等方向的研究。

TP24

A

10.16086/j.cnki.issn1000-0380.201509004

修改稿收到日期：2015-05-13。