无线传感器网络节点自适应加权定位算法

刘 政

(桂林航天工业学院自动化系，广西 桂林 541004)

无线传感器网络节点自适应加权定位算法

刘 政

(桂林航天工业学院自动化系，广西 桂林 541004)

为了提高无线传感器网络节点定位精度，提出一种自适应加权定位算法。首先将距离加权因子拆分为独立加权因子，为独立加权因子匹配修正系数，修正系数根据测距距离做自适应调整，最后验证独立加权因子的自适应修正系数与基于接收信号强度的测距距离的数学关系。仿真试验结果表明，在同等测距误差前提下，独立加权因子的自适应修正能够显著降低平均定位误差，提高定位精度。

无线传感器网络(WSN) 定位算法 加权质心 修正系数 接收信号

0 引言

节点定位是无线传感器网络的一项关键技术[1-3]，从定位手段上看，目前的定位算法主要基于测距和非测距。测距是通过测量节点间的距离或角度信息，使用三边测量、三角测量或最大似然估计[4]计算节点位置。常用的测距技术有：接收信号强度指示[5]、到达时间差、到达角度等。非测距不需要距离和角度信息，根据网络连通性[6]等信息来实现定位。常用的非测距技术有质心算法[7]、近似三角形内点测试算法[8]等。

关于节点定位的研究已有一些成果，文献[9]先用极大似然估计对定位节点进行粗略估计，再用加权质心求精；文献[10]对信标节点通信交集区域构成的三角形求质心；文献[11]根据节点距离的远近，增加加权系数来调整加权影响力；文献[12]～[13]先建立信号传播模型，再离散划分定位区域,并用高斯拟合求精。本文提出一种自适应调整距离加权的定位算法，该算法实现原理简单，整体开销较小，能够满足WSNs低功耗的需求。

1 加权质心定位原理

如果用多个信标节点定位未知节点，该未知节点一定处于多个信标节点的感知信号交集。三边测量法如图1所示，若采用三边测量法计算，前提必须保证三个信标节点的感知圆圈相交于一点(定位节点)。

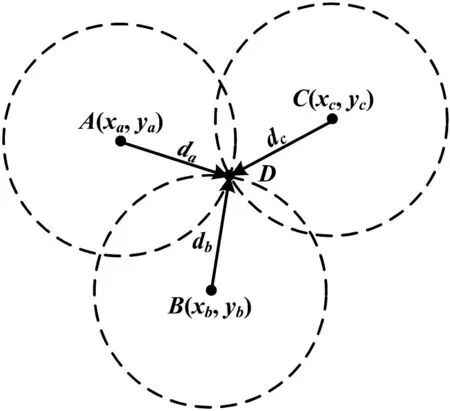
图1 三边测量法示意图Fig.1 Schematic diagram of the trilateration measurement

存在下列公式：

(1)

由此可以得到未知节点D的坐标为：

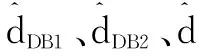
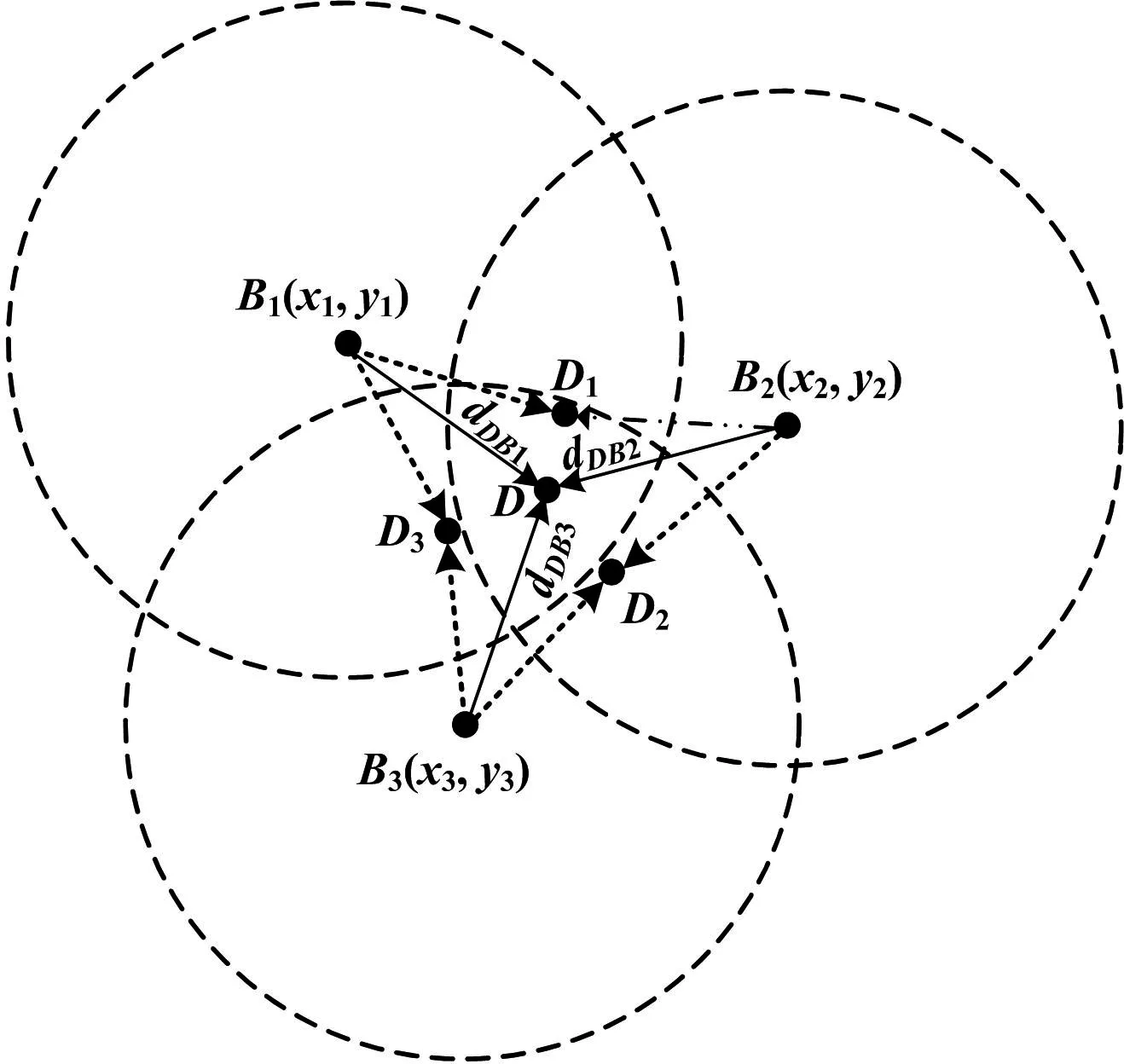
图2 加权质心示意图Fig.2 Sketch map of the weighted centroid

根据未知节点D到信标节点B1、B2的测距距离，得到距离与坐标的数学模型：

(2)

(3)

(4)

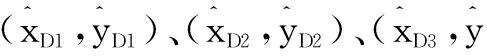
(5)

加权质心为每一个测距坐标增加了距离加权，通过加权因子来体现各个信标节点对质心坐标决定权的大小，并利用加权因子来体现各信标节点对质心位置的影响程度。

由式(5)可知，将距离之和的倒数作为加权因子，仅反映出质心三角形中未知节点和两个信标节点总的距离关系，显然没有区分不同距离的信标节点影响力。

2 自适应加权调整

通常情况下，两个信标节点与未知节点的实际距离不可能完全一致，离未知节点越近的信标节点获得的距离加权越大，离未知节点越远的信标节点获得的距离加权越小。在算法中应该体现信标节点对未知节点的离散化加权影响，故拆分距离加权是算法改进的切入点。

拆分式(5)中的加权因子：

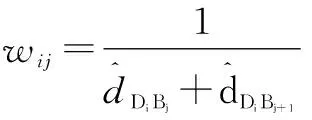
(6)

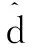
差异化距离加权的影响力，为式(6)增加加权修正系数K。

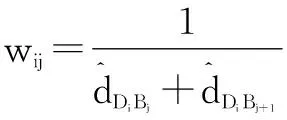
(7)

式(5)修正为式(8)：

(8)

加权修正系数K受到当前信标节点与未知节点距离差异的影响。从式(8)抽取任意一个信标节点Bs(x,y)，分析加权修正系数K的变化对定位效果的影响。

(9)

式中：Pi,s(x,y)为信标节点Bs(x,y)对未知节点Di(x,y)的定位影响力。衡量影响力的变化可以通过计算Pi,s(x,y)对K求导的正负性判断。

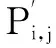
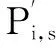
3 算法流程

无线传感器网络节点自适应加权定位算法流程如下。

① 信标节点周期性发送节点ID、自身位置信息P。

④ 未知节点选择集合ωΒ中RSSI值排在前三的信标节点构成如图1或图2所示的邻居质心三角形。如果不满足，则选择RSSI值排在第四的信标节点，以此类推直到满足图1或图2的邻居质心三角形。加权修正系数K从1开始递增，由式(8)计算得到一组未知节点位置坐标群。

⑤ 计算平均定位误差，找到误差最小时对应的加权修正系数K。

⑥ 利用加权修正定位式(8)重新计算坐标，完成定位。

4 仿真结果与分析

在Matlab环境中，对改进算法进行仿真分析。为了更贴近实际环境，在测试中我们设置仿真区域为50m×50m大小的平面区域，50个未知节点的位置随机分布，20个信标节点均匀随机分布，节点的通信半径为20m。信标节点感知未知节点的测距误差为0～20%中的一个随机数。

4.1RSSI值与测距距离的拟合

在实际的试验中，我们设定1m、5m、10m、15m、20m作为参考测量距离点，在每个距离点通过RSSI测距100次，求出平均值作为RSSI值。统计实际测量中的RSSI数据和距离，确定实际环境中的RSSI测距传输函数[12]。

RSSI(d)=-39.86-10×2.17×lgd

(10)

然后对这些数据按照对数常态分布模型进行最小二乘法拟合，拟合曲线如图3所示。

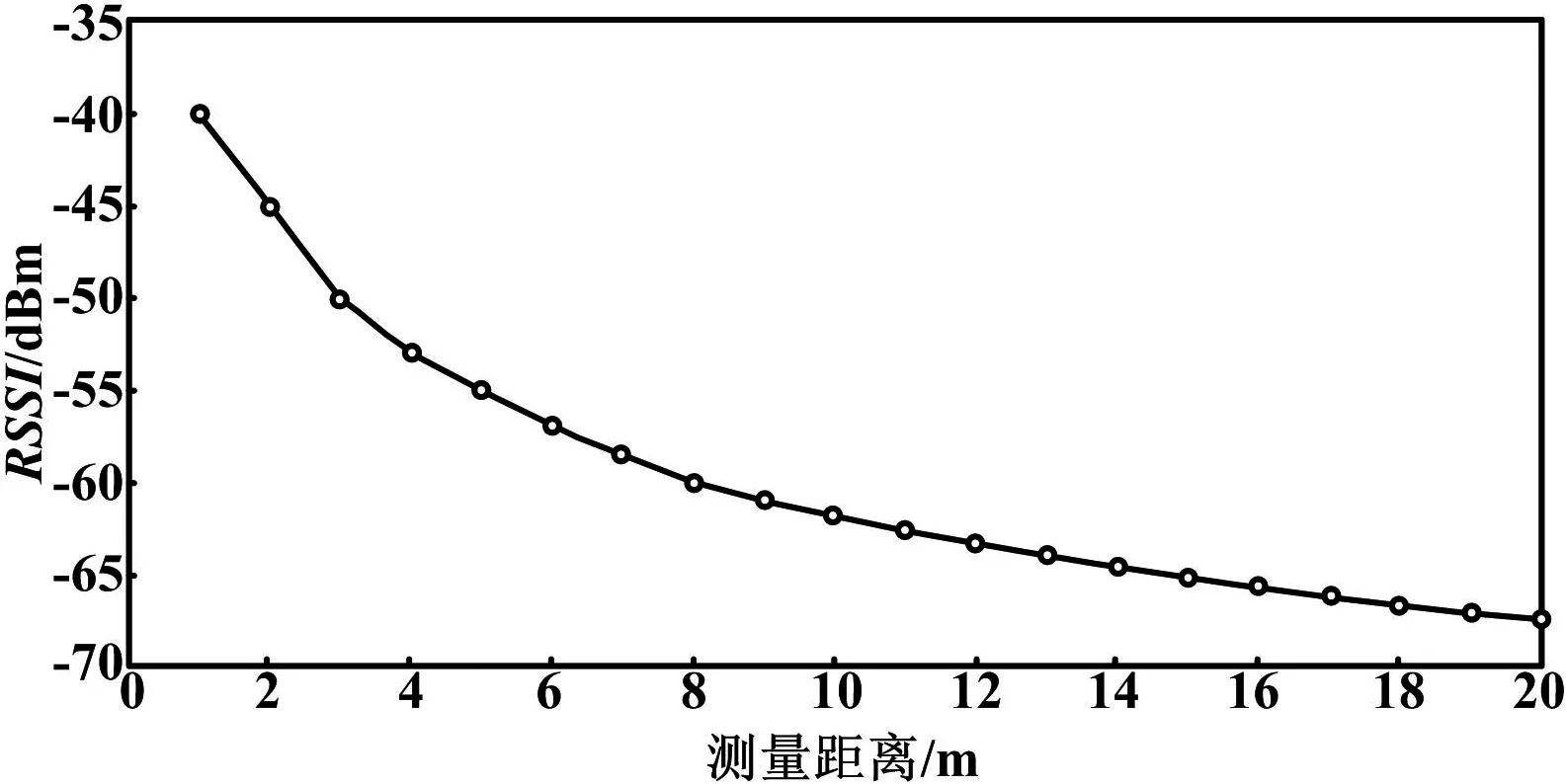
图3 RSSI与测距距离拟合曲线Fig.3 Fitting curve of RSSI and ranging distance

4.2 修正系数对定位误差的影响

为验证改进算法性能，将本文改进定位、质心定位、加权质心的定位误差进行比较。定位误差指的是通过定位计算得到未知节点的估计位置与实际位置的偏差。这种偏差可以用两者之间的欧氏距离除以节点的通信半径来衡量，利用平均定位误差来衡量定位算法的优劣。

在同一网络环境下重复试验100次，每次试验都将所有节点重置，并对100次测距误差求均值。

节点定位误差计算如式(11)所示：

(11)

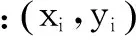
对N个未知节点的定位误差求平均，得到平均定位误差为：

(12)

平均定位误差与修正系数示意图如图4所示。

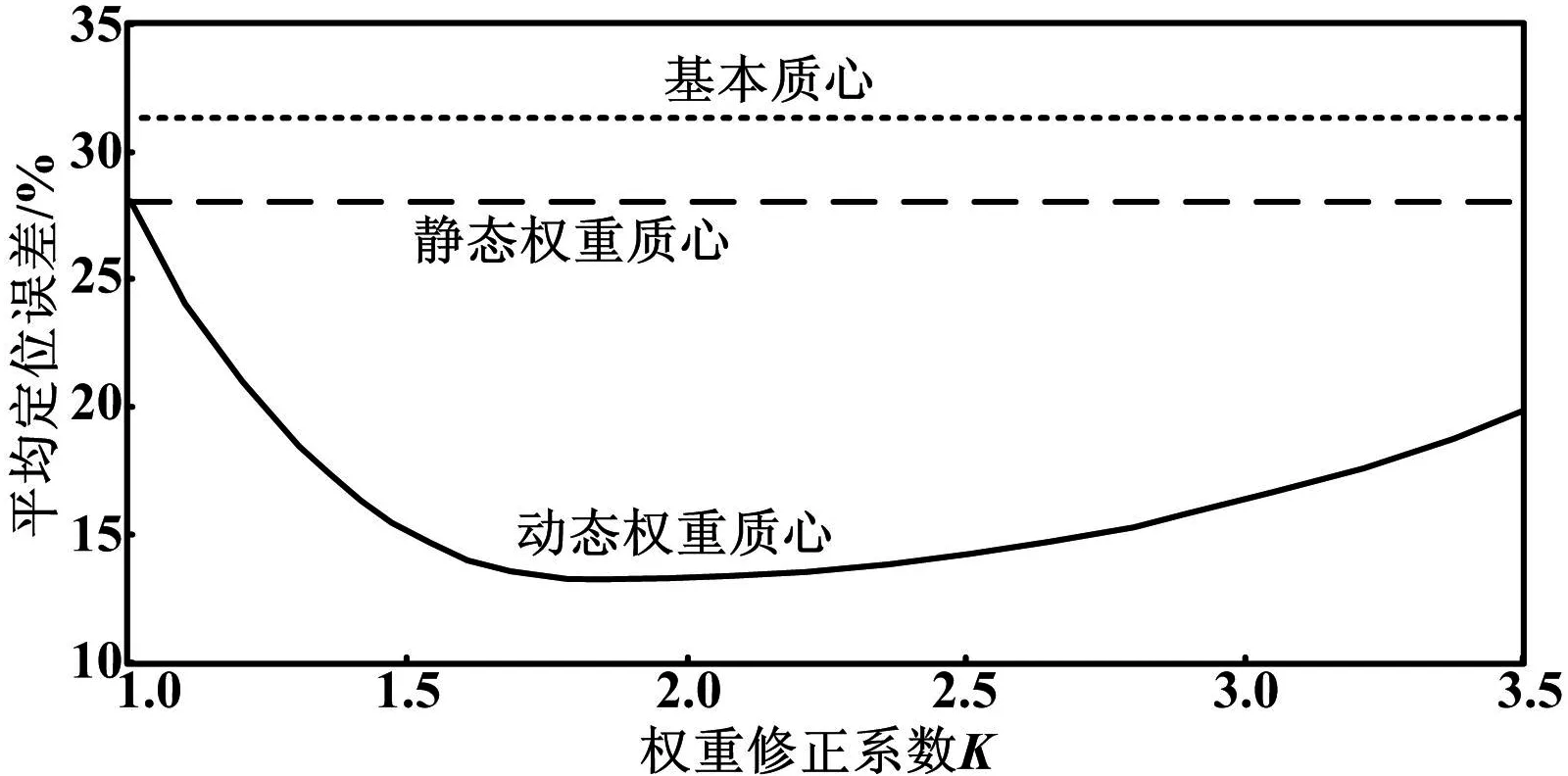
图4 平均定位误差与修正系数示意图Fig.4 Average locating error and correction factor

观察图4中的加权修正系数K的变化对平均定位误差造成的影响，可以看出，改进算法的平均定位误差明显优于基本质心和加权质心。

4.3 信标分布密度对定位误差的影响

信标节点密度是WSNs定位的重要参数, 信标节点数量的增减会直接影响定位精度。若算法性能要求苛刻，需配置更多数量的信标节点，但是会直接导致WSNs的应用成本大幅度提高，限制其大范围的推广。所以这里仿真验证信标节点分布密度对定位误差的影响，为检验本文改进算法的最优性能，取K=1.9，分析未知节点的邻居信标节点数量对平均定位误差的影响。定位误差与信标节点个数示意图如图5所示。

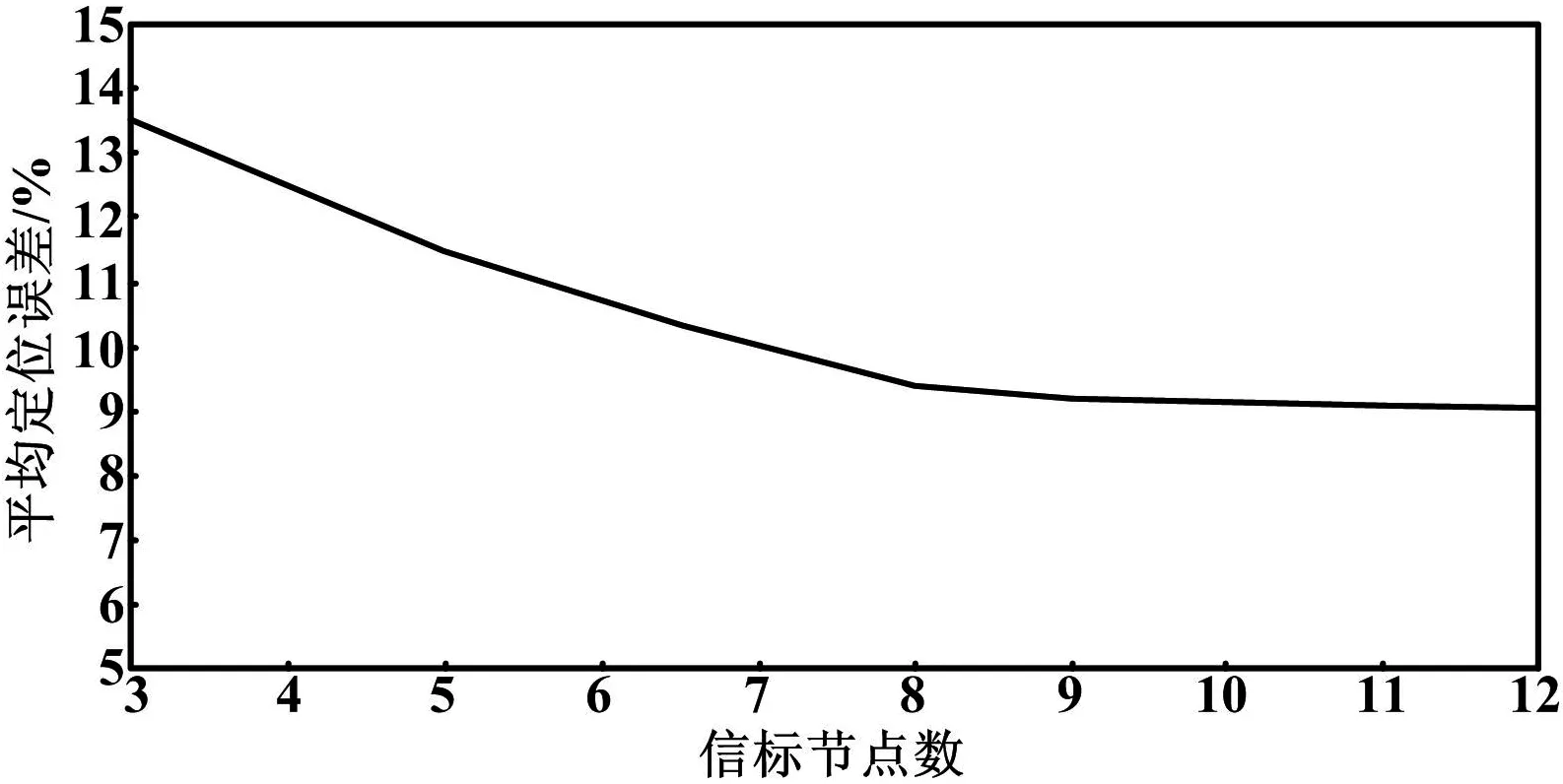
图5 定位误差与信标节点个数示意图Fig.5 Locating error and number of beacon nodes

5 结束语

本文在加权质心定位原理基础上，将距离加权因子拆分成独立加权因子，并为距离加权因子匹配修正系数K，K在自适应调整中找到最小定位误差。该算法不存在多维度矩阵的运算和复杂的迭代计算，可以满足传感器网络中对位置精度要求不太苛刻的需求。下一步的改进思路：建立信标节点对未知节点RSSI测距值与加权系数动态选择的数学模型，根据RSSI值大小动态划分定位中心区域和边缘区域，尝试获取中心区域和边缘区域的分区域加权系数动态选择计算模型。

[1] Jonathan B,Adam M.Localization in sensor networks[M].Handbook of Sensor Networks:Algorithms and Architectures.USA:Wiley-Interscience,2005:277-310.

[2] Arampatzis T,Lygeros J,Manesis S.A survey of applications of wireless sensors and wireless sensor networks[C]∥Proceedings of the 2005 IEEE International Symposium on,Mediterrean Conference on Control and Automation,2005:719-724.

[3] Akyildiz I,Su W,Sankarasvbramaniam Y.A survey on sensor networks[J].IEEE Communications Magazine,2011,40(8):102-l14.

[4] 温立.无线传感器网络定位技术研究[D].上海：复旦大学,2008:34-37.

[5] Luthy K A,Grant D,henderson T C.Leveraging RSSI for robotic reapair of disconnected wireless sensor networks[C]// 2007 IEEE International Conference on Robotics and Automation,Rome,Italy,2007:10-14.

[6] Nirupama B,John H,Deborah E.GPS less low cost out door localization for very small devices[J].IEEE Personal Communications(S1070-9916),2000,7(5):28-34.

[7] Niculescu D,Nath B.DV based positioning in Ad Hoc networks[J].Journal of Telecommunication Systems(S1572-9451),2003,22(4):267-280.

[8] He T,Huang C,Blum B M,et al.Range free localization schemes for large scale sensor networks[C]//ACM International Conference on Mobile Computing and Networking(MobiCom).San Diego,California,USA:ACM Press,2003:81-95.

[9] 韩江洪,祝满拳,马学森，等.基于RSSI的极大似然与加权质心混合定位算法[J].电子测量与仪器学报,2013,27(10):937-943.

[10]丁恩杰,乔欣,常飞,等.基于RSSI的WSNs加权质心定位算法的改进[J].传感器与微系统,2013,32(7):53-56.

[11]胡咏梅,张欢.一种改进的无线传感器网络质心定位算法[J].计算机工程与科学,2012,34(2)：45-49.

[12]陶志勇,路笋.基于ZigBee的修正加权质心定位算法研究与实现[J].计算机应用与软件,2014,31(1)：123-126.

[13]詹杰,刘宏立,刘述钢,等.基于RSSI的动态加权定位算法研究[J].电子学报,2011,39(1):82-88.

[14]党小超,李小艳.无线传感器网络节点定位加权校正模型[J].计算机应用,2012,32(2):355-358.

Adaptive Weighted Locating Algorithm for Wireless Sensor Network Nodes

In order to enhance the node locating accuracy for wireless sensor network, the adaptive weighted locating algorithm is proposed. Firstly, the distance weighting factor is split into independent weighting factors, and the correction coefficients are matched for independent weighting factors, the correction coefficients are adapted in accordance with the distance measured, finally the mathematical relationship between the adaptive correction coefficient of the independent weighing factor and the distance measured based on

signal strength is verified. The result of simulation experiment shows that under the same level of distance measuring error, the adaptive correction of the independent weighing factor can reduce the average locating error significantly for improving the locating accuracy.

Wireless sensor network(WSN) Locating algorithm Weighted centroid Correction coefficient Received signal

国家自然科学基金资助项目(编号：61202007)；

广西教育厅科研基金资助项目(编号：201106LX718)；

桂林航天工业学院基金资助项目(编号：YJ1302)。

TP393

A

10.16086/j.cnki.issn1000-0380.201506001

修改稿收到日期：2014-12-04。

作者刘政(1981-)，男，2007年毕业于桂林理工大学检测技术与自动化装置专业，获硕士学位，讲师；主要从事无线传感器网络、智能仪器方面的研究。