推挽变压器工作过程的分析及其仿真

伍家驹，胡航，施红军，张树国

（南昌航空大学信息工程学院，江西南昌330063）

目前，常见的逆变电路分为两大类，桥式逆变电路和推挽式逆变电路：桥式逆变电路具有双向励磁、无直流偏磁等优点，因此对其工作过程的分析及建模较为容易，但桥式逆变电路结构复杂、成本高、可靠性低以及驱动电路复杂，尤其致命的缺点是交-直流不能分隔，需加一个变压器使其分隔；而推挽式逆变电路具有交-直流分隔、器件少且体积小、便于控制输入输出电压/电流、驱动电路简单等优点，但因其具有直流偏磁问题，且磁性材料具有多值非线性，在分析建模及工程实践应用中，相关参数难以获取［1］，也难以达到数学分析、仿真和实验三者相统一，故有关推挽式电压型逆变器工作模态的分析和建模仿真的报道尚属鲜见。如文献［2-4］中主要讨论了推挽变压器的漏感，虽也有建模仿真，但并没有对推挽式逆变器的各工作模态进行分析；文献［5］中研究的是三管式推挽电路的工作效率；文献［6］中研究的是如何提高推挽式功率变换器的工作电压；文献［7-9］中主要介绍了电子变压器的磁芯、线圈和变压器设计，但并没有对推挽式逆变器的各工作模态进行分析，也没有对其进行建模仿真。因此不但有碍于多线圈电子变压器的研究以及对其内部结构的改进、还有碍于交流、高频、单相/三相等其它变换器控制系统的研制。

文中分析了推挽式电压型SPWM 逆变器的各种工作模态，以及在不同模态下逆变器的回路方程，综合各回路方程建立了逆变器的数学模型，并基于该模型用Matlab 进行仿真，用数学分析和实验结果验证了仿真结果的正确性。

1 推挽式逆变器主回路

推挽变压器及其周边器件如图1所示。

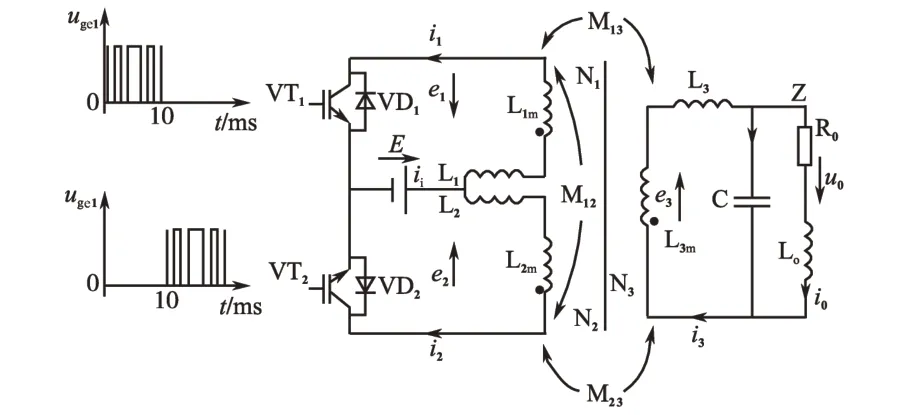
图1 推挽式电压型SPWM逆变器主回路Fig.1 The main circuit of basic push-pull voltage source SPWM inverter

推挽变压器的一次侧由线圈N1和N2共同构成，二次侧由线圈N3构成；Lim为线圈Ni的自感，Mij为线圈Nj-Ni间的互感，Li为Ni的“动态有效漏感”，ei为电动势，其中i，j={1，2，3}；全控器件VTi的电流iVTi=ii，二极管VDi的电流iVDi=-ii。在信号ugei和负载Z的作用下，SPWM脉冲功率序列可实现电磁能量定向可控的传输，从而达到隔直、低通滤波和波形控制等目的。图1 中上下2 个IGBT管的开关过程电压分别为Uce1和Uce2。

2 推挽式逆变器的数学模型

2.1 推挽变压器的工作过程

2.1.1 开关工作模态1

在0～10 ms 时 间 内，VT1导 通 时，E→L1→L1m→VT1→E构成回路，如图2所示。

图2 VT1导通时的逆变器回路图Fig.2 The circuit of inverter when VT1 switching on

此时，L1和L3发生作用，L1为N1的动态有效漏感，其持续的时间为VT1的导通瞬间，约为100 ns，过程较短；L3为N3的动态有效漏感，其持续时间为VT1导通后到其截止前的时间，过程相对较长。L1和L3涉及空间为线圈N1和N3，而线圈N2中涉及的漏感L2不发生作用，其仅在一次线圈中N1和N2的电流i1，i2换流的瞬间发生作用，作用过程非常短暂。从而形成了电路中能量的传输方向及其回路为：E→VT1→N1→N3→L3→C//Z，其中i1与i3的流向均与参考方向相同，回路方程为

2.1.2 开关工作模态2

在0～10 ms 时间内，VT1截止时，由于电路中的能量不能突变即电流i1不能突变，因此电路中的能量需要形成新的回路进行释放，VD2导通续流。因i1是从标记端流入，故有：L2m→L2→E→VD2→L2m的能量释放回路如图3所示。

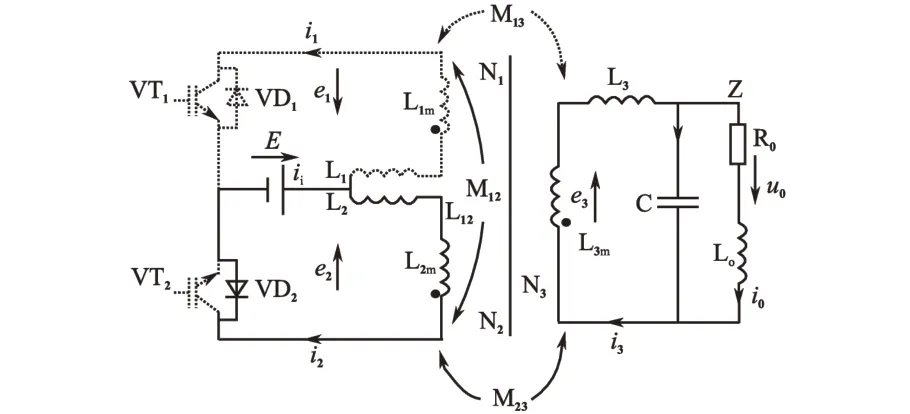
图3 VT1截止时的逆变器回路图Fig.3 The circuit of inverter when VT1 switching off

此时，L2和L3发生作用，L2为N2的动态有效漏感，其持续时间为VT1截止到VD2导通续流之前的瞬间，约为200 ns，过程较短；L3持续时间为VD2导通续流之后到其截止之前的时间，过程相对较长。L2和L3涉及空间为线圈N2和N3，而线圈N1中涉及的漏感L1不发生作用，其仅在一次线圈中N1和N2的电流i1，i2换流的瞬间发生作用。电路中的能量回馈给电源，其能量传输方向为：C//Z→L3→N3→N2→VD2→E，其中i2的流向与参考方向相反，i3的流向与参考方向相同，回路方程为

2.1.3 开关工作模态3

在10～20 ms 时间内，VT2导通时，E→L2→L2m→VT2→E构成回路如图4所示。

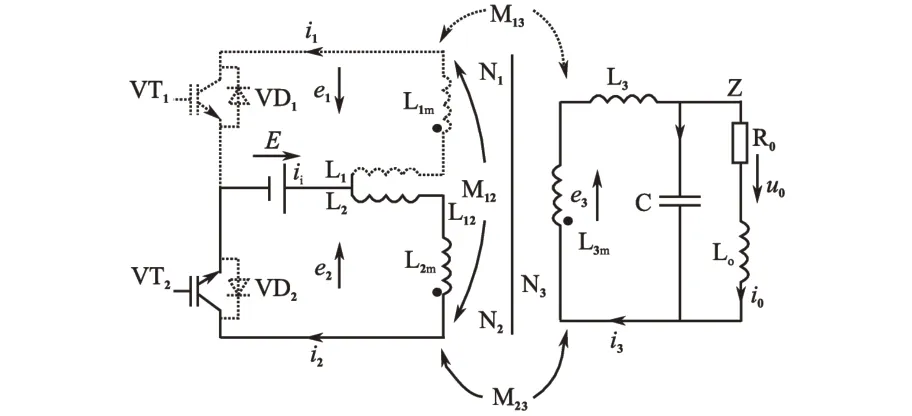
图4 VT2导通时的逆变器回路图Fig.4 The circuit of inverter when VT2 switching on

此时，L2和L3发生作用，L2持续的时间为VT2导通瞬间，约为100 ns，过程较短；L3持续时间为VT2导通后到其截止之前的时间，过程相对较长。L2和L3涉及空间为线圈N2和N3，而线圈N1中涉及的漏感L1不发生作用，其仅在一次线圈中N1和N2的电流i1，i2换流的瞬间发生作用，作用过程非常短暂。电路中能量的传输方向为：E→VT1→N2→N3→L3→C//Z，其中i2的流向与参考方向相同，i3的流向与参考方向相反，回路方程为

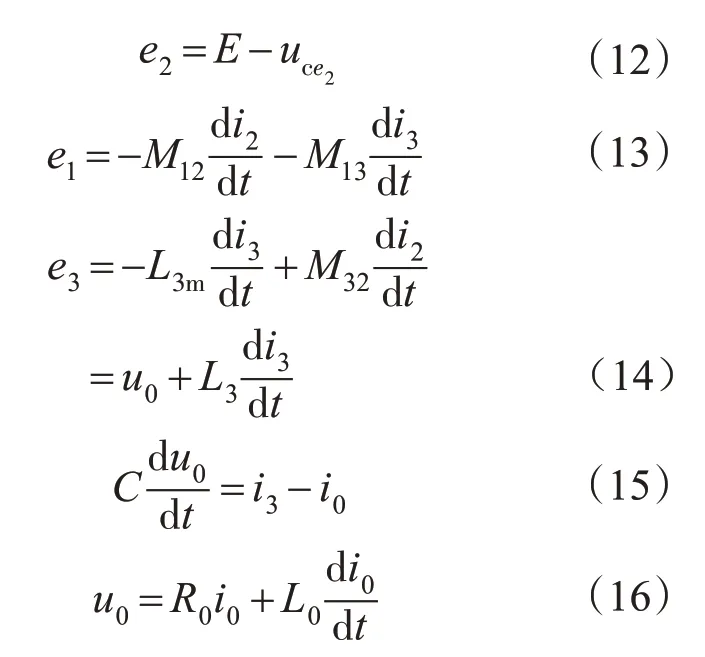
2.1.4 开关工作模态4

在10～20 ms时间内，VT2截止时，由于电路中的能量不能突变即电流i2不能突变，因此电路中的能量需要形成新的回路进行释放，VD1导通续流。因i2是从标记端流出，故有：L1m→L1→E→VD1→L1m的能量释放回路如图5所示。

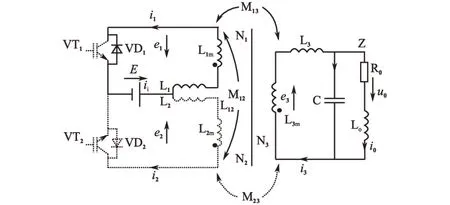
图5 VT2截止时的逆变器回路图Fig.5 The circuit of inverter when VT2 switching off

此时，L1和L3发生作用，L1持续的时间为VT2截止到VD1导通续流之前的瞬间，约为200 ns，过程较短；L3持续时间为VD1导通续流之后到其截止之前的时间，过程相对较长。L1和L3涉及空间为线圈N1和N3，而线圈N2中涉及的漏感L2不发生作用，其仅在一次线圈中N1和N2的电流i1，i2换流的瞬间发生作用，作用过程非常短暂。电路中的能量回馈给电源，其能量流向为：C//Z→L3→N3→N1→VD1→E，其中i1与i3的流向均与参考方向相反，回路方程为

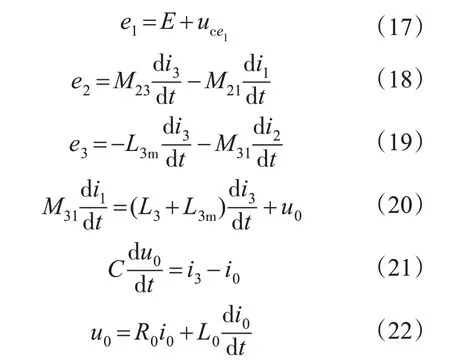
在整个周期内，电路中的能量守恒（忽略器件损耗，计为理想情况），由式（1）～式（22）可得：

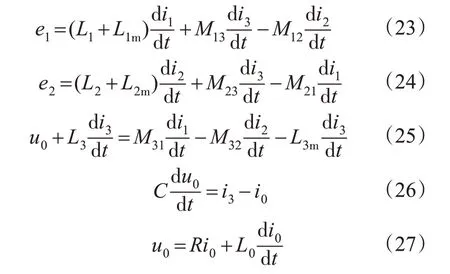
2.2 推挽式逆变器的数学模型

取式（23）～式（27）的i1，i2，i3，u0和i0为状态变量，则可得到下式：

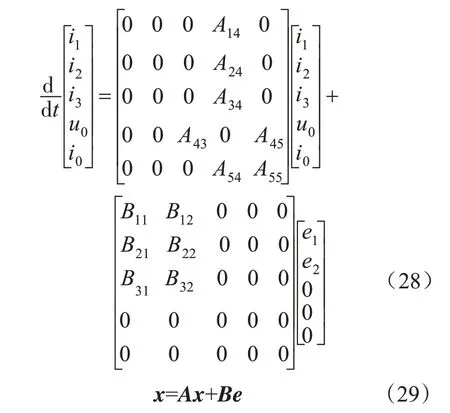
其中

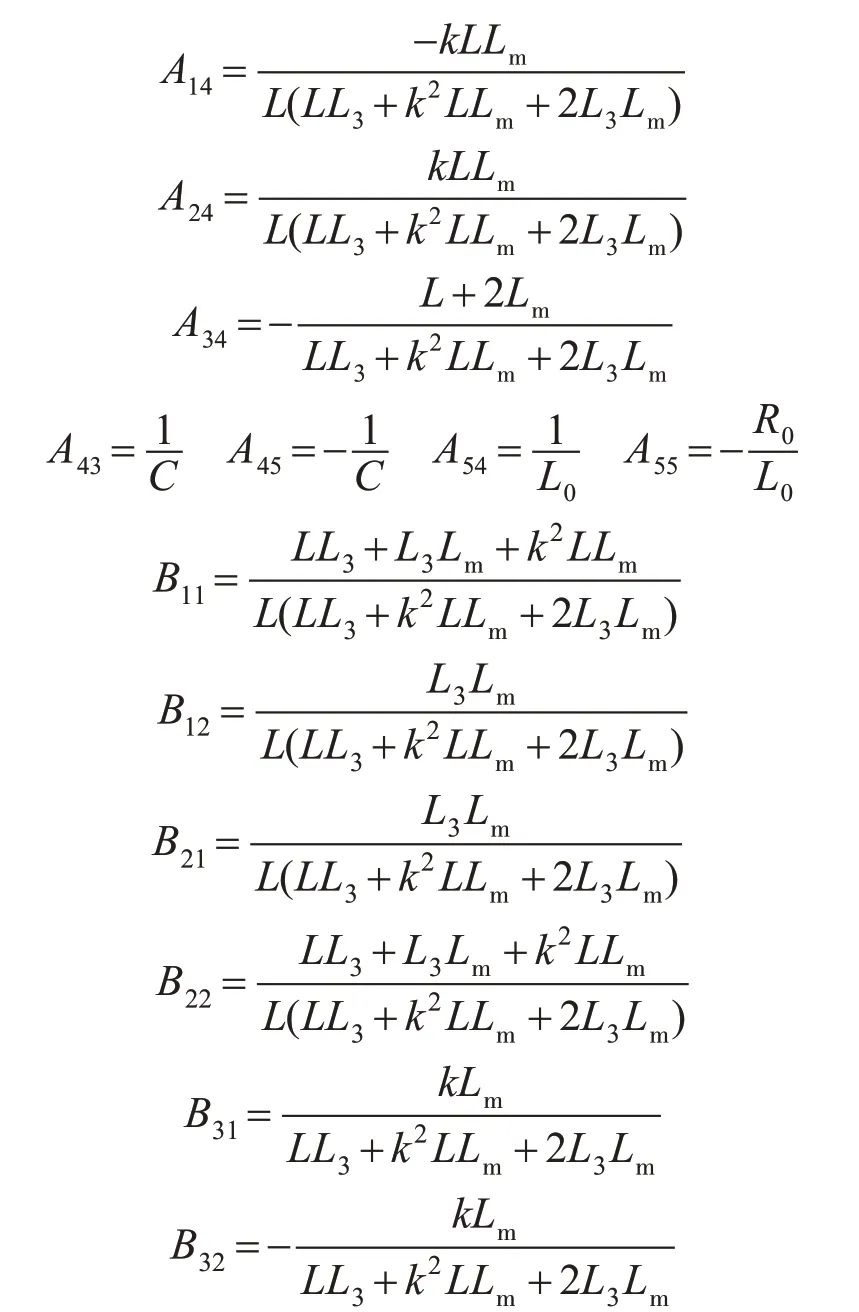
推挽式电压型SPWM 逆变器的相关元器件参数为：W1=W2=12 匝，W3=206 匝，E=24 V，k=W3/W1；L1m=L2m=Lm=M12=M21=6.6 mH，L3m=k2Lm=1.89 H；L1=L2=L=1.9 μH，L3=6.2 mH；M13=M23=kLm=110 mH；C=8 μF，负载Z的功率因数为0.8时，R0=38 Ω，L0=92 mH；载波为三角波且频率为10 kHz，调制波为正弦波；输出频率为50 Hz，输出电压为220 V，输出功率为1 kW。

把已知的元器件参数代入式（28），则可得推挽式电压型SPWM逆变器的状态方程为

3 仿真和实验

在对推挽式逆变器进行仿真之前需设置对本系统适用的仿真参数，才能使仿真波形与实验波形达到相吻合的目的。定步长Fixed-step size设置为100 ns时，就可在仿真波形中体现出IGBT导通的时间；算法设置为ode5，采样Sampling 中选Decimation 1 时，可观察到波形的细微变化。实验所使用的示波器型号为Tektronix3032B，示波器附属电流探头型号为TektronixA622。

逆变器输入电流的仿真与实验波形如图6、图7所示。

图6 变压器输入电流ii的仿真波形Fig.6 Simulation waveform of input current ii

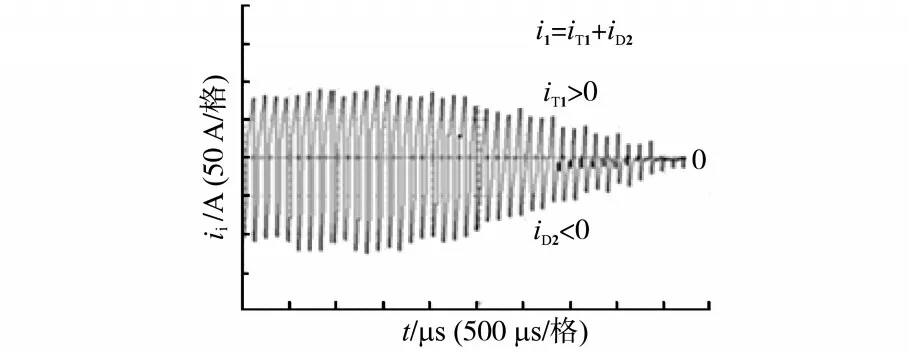
图7 变压器输入电流ii的实验波形Fig.7 Experimental waveform of input current ii

图6 、图7 展示了变压器输入电流波形，由于电源E 的方向是不变的，从电流的方向及其变化趋势可分辨出能量输送与回馈。

IGBT 开关过程电压的仿真与实验波形如图8、图9所示。

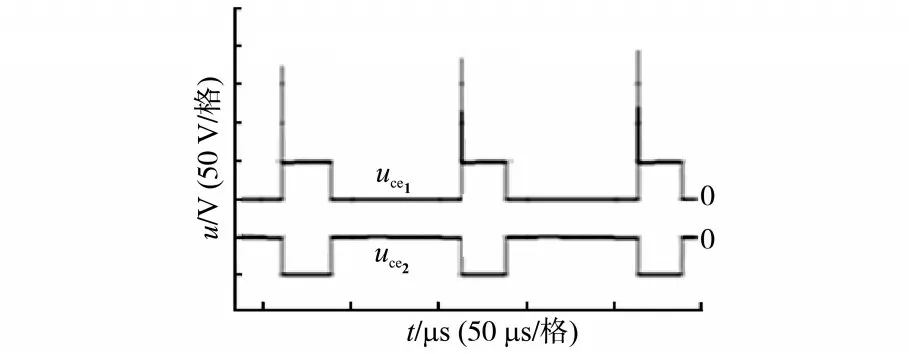
图8 uce1，uce2的仿真波形Fig.8 Simulation waveforms of uce1，uce2

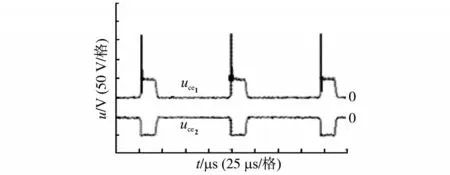
图9 uce1，uce2的实验波形Fig.9 Experimental waveforms of uce1，uce2

图8 、图9 展示了由于一次侧两线圈换流时使得动态有效漏感L1或L2起作用而产生的过电压L1（di/dt）或L2（di/dt），但过电压只增加全控型器件IGBT 的电压应力，而对不可控型器件二极管无影响。故对表示IGBT处于反复通断状态区间的uce1而言，L1（di/dt）会产生过电压，而对表示续流二极管处于反复通断状态区间的uce2而言，无电压应力过大之忧；同理，对表示IGBT处于反复通断状态区间的uce2而言，L2（di/dt）会产生过电压，而对表示续流二极管处于反复通断状态区间的uce1而言无电压应力过大之忧。

4 结论

1）推挽式电压型SPWM 逆变器在不同开关状态下，构成各自的工作模态，推挽变压器诸漏感存在着不同的作用时间和涉及空间，即开关器件的通断状态决定着漏感的有效时间，线圈间能量的流向决定着漏感的作用时间。

2）基于各工作模态下推挽式逆变器的回路方程，可建立该逆变器的数学模型，用Matlab 对其进行仿真，达到了数学分析、仿真和实验三者相统一的效果，验证了该数学模型及其参数辨识方法的正确性。

3）本文中研究的推挽式逆变器的各工作模态，有利于设计低损耗无源吸收电路；建立的该逆变器的数学模型，可为其他多线圈电子变压器的研究提供参考，亦可为交流、高频、单相/三相等其它变换器控制系统工作原理的分析和建模仿真提供参考。

［1］ 伍家驹.逆变器理论及其优化设计的可视化算法［M］.北京：科学出版社，2012.

［2］ 伍家驹，杉本英彦，余达祥，等.一种间接测算推挽变压器漏感的新方法［J］.中国电机工程学报，2005，25（12）：129-137.

［3］ 伍家驹，杉本英彦.一种用于推挽式电压型逆变器的低损耗无源吸收电路［J］.中国电机工程学报，2006，26（11）：93-101.

［4］ 伍家驹，刘桂英，陈琼，等.推挽变压器的一种外特性模型［J］.电工技术学报，2011，26（3）：123-138.

［5］ 袁义生，伍群芳.并联LC 网络的软开关三管推挽式直流变换器［J］.中国电机工程学报，2013，33（24）：42-51.

［6］ Wong Pit-Leong，Xu Peng，Yang Bo，et al.Performance Improvements of Interleaving VRMs Withcoupling Inductors［J］.IEEE Transactions on Power Electronics，2001，4（16）：499-507.

［7］ 张占松，蔡宣三.开关电源的原理与设计［M］.修订版.北京：电子工业出版社，2005.

［8］ Hurley W G，Wölfle W H.Transformers and Inductors for Power Electronics：Theory，Design and Applications［M］.John Wiley&Sons，2013.

［9］ Valchev V C，Van den Bossche A.Inductors and Transformers for Power Electronics［M］.CRC press，2011.